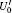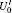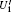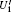†Corresponding author. E-mail: wangchaopaper@126.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61272501, 61272514, 61170272, 61472048, 61402058, 61121061, and 61411146001), the Program for New Century Excellent Talents in University of China (Grant No. NCET-13-0681), the National Development Foundation for Cryptological Research (Grant No. MMJJ201401012), the Fok Ying Tong Education Foundation (Grant No. 131067), the Natural Science Foundation of Beijing (Grant Nos. 4132056 and 4152038), the Postdoctoral Science Foundation of China (Grant No. 2014M561826), and the National Key Basic Research Program, China (Grant No. 2012CB315905)
This study proposes two novel fault tolerant deterministic secure quantum communication (DSQC) schemes resistant to collective noise using logical Bell states. Either DSQC scheme is constructed based on a new coding function, which is designed by exploiting the property of the corresponding logical Bell states immune to collective-dephasing noise and collective-rotation noise, respectively. The secret message can be encoded by two simple unitary operations and decoded by merely performing Bell measurements, which can make the proposed scheme more convenient in practical applications. Moreover, the strategy of one-step quanta transmission, together with the technique of decoy logical qubits checking not only reduces the influence of other noise existing in a quantum channel, but also guarantees the security of the communication between two legitimate users. The final analysis shows that the proposed schemes are feasible and robust against various well-known attacks over the collective noise channel.
Quantum communication, known as a kind of theoretically unconditionally secure communication mode, has attracted enormous attention in recent years. Since a pioneering quantum key distribution (QKD) protocol was put forward by Bennett and Brassard in 1984, called the BB84 protocol, [1] more and more works have been focused on this field and various kinds of QKD protocols[2– 8] have been presented. In a QKD protocol, the random shared secret key is established first through a quantum channel and then utilized to encrypt the transmitted message between two remote authorized parties. Another remarkable research field, quantum direct communication (QDC) which includes quantum secure direct communication (QSDC)[9– 19] and deterministic secure quantum communication (DSQC), [20– 30] has also been developed quickly.
Different from QKD, QDC provides a new means to communicate the secret message directly without creating a random shared key to encrypt it in advance. In 2002, Long and Liu proposed an efficient QKD scheme based on quantum data blocks, which can also be recognized as the first QSDC protocol.[19] Later, another two-step QSDC protocol exploiting the quantum dense coding was proposed by Deng and Long in 2003, which is the first truly secure QSDC protocol, and a criterion for QSDC was provided in this protocol.[10] After that, the extensive QSDC protocols[11– 19] are presented and the idea of QSDC has been realized in many quantum communication systems. Especially, in DSQC the legitimate receiver can instantaneously obtain the deterministic information after exchanging one round of classical communication. In 1999, Shimizu and Imoto[20] proposed the first DSQC protocol, and another DSQC protocol based on single photon two-qubit states was presented by Beige et al.[21] in 2002. Thereafter, many advanced DSQC protocols have been introduced utilizing the entangled quantum states.[22– 30]
However, these protocols can only work well under an ideal condition that the quantum channel is noiseless. Actually, the channel noise is inevitable. In a practical transmission process, the quantum channel is always influenced by thermal and mechanical fluctuations of some medium (e.g., the optical fiber), which tends to produce channel noise. Generally speaking, the channel noise not only changes the fidelity of the quantum states carrying the information, which will decrease the successful probability of the schemes, but also gives the eavesdropper a chance to disguise her disturbance with a better fiber, which will directly affect the security of the quantum communication.[31] The practical experiments show that the fluctuation is always slow in time. Therefore, if the qubits travel inside a time window shorter than the variation of the noise sources, these qubits will be affected by the identical noise, which is known as the collective noise.[32, 33] Thus, at present, it is always suppose that the channel noise is a collective one in quantum cryptography communication.
In order to overcome the noise disturbance, one needs to design new fault tolerant protocols over the noisy channel or new physical channels for implementing the original protocols. Now, there are two valid solutions to deal with such a problem: one way is to design a new protocol with a higher channel error rate threshold, such as the results presented in Refs. [34] and [35]; the other way is first to construct an appropriate channel noise model and then find a resolvent accordingly to reduce or eliminate the quantum channel noise, such as a quantum error correct code (QECC), [36] single-photon error rejection, [37] and decoherence-free (DF) subspace.[38, 39] Among these proposed methods, DF subspace is an important one since it can be made up of several physical qubits experiencing the identical noise and keep invariant over a collective-noise channel. Therefore, DF subspace is frequently used in quantum communication to implement a fault-tolerance communication. Varieties of quantum cryptographic protocols against collective noise have been developed quickly, including QKD, [31– 33, 40– 44] QSDC, [45– 50] and quantum secret sharing (QSS), [51– 55] etc.
However, compared to those fields, so few DSQC protocols over a collective noise channel have been published.[56– 59] In fact, DSQC has some advantages over QSDC in a practical channel. The major advantage is that the qubits carrying the secret message are not transmitted again after the eavesdropping check in DSQC, which will make DSQC more secure than QSDC over a noisy channel and make DSQC more convenient for quantum error correction. In 2009, Dong et al.[56] presented a DSQC scheme against collective-dephasing noise by using EPR pairs and auxiliary photons, without giving the corresponding scheme against collective-rotation noise. And, in the same year, Gu et al.[57] proposed two DSQC protocols exploiting three-photon entangled states over a collective-dephasing noise channel and a collective-rotation noise channel, respectively. Then, in 2013, by taking advantage of the GHZ state and GHZ-like state, Yang et al.[58] designed two DSQC protocols, each of which is robust under one kind of collective noise: collective-dephasing noise, and collective-rotation noise, respectively. Just recently, Yuan et al. carefully investigated four special two-qubit entangled states and presented a new DSQC protocol against collective rotating noise based on order rearrangement of photon pairs.[59]
Different from the above-mentioned DSQC protocols, in this work, two fault tolerant DSQC schemes against collective noise, i.e., the collective-dephasing noise and the collective-rotation noise, respectively, are put forward based on the logical Bell states for the first time. By merely using the property of logical Bell states immune to collective-noise, two novel coding functions are designed, each of which can be applied to construct the corresponding DSQC scheme. In the proposed DSQC schemes, the sender, Alice, only performs two simple unitary operations on the corresponding qubits of the prepared logical Bell states to encode the transmitted secret message. The receiver, Bob, can decode the secret information by performing Bell measurement after the additional classical bit is exchanged between two legitimate users. In practical application, these encoding and decoding operations can be realized easily, and the logical Bell states, as the quantum resource, are verified to be feasible in experiment. More importantly, the proposed schemes combine the one-step quanta transmission strategy and the decoy logical qubits checking technique, which can effectively reduce the influence of other noise existing in the quantum channel, and further guarantee the unconditional security against various kinds of attacks, such as the information leakage attack, the intercept-resend attack, the entangle-measure attack, the correlation– elicitation attack, and the Trojan horse attack, etc.
The structure of the rest of the paper is organized as follows. In Section 2, we first introduce the related works. Then, we construct two new coding functions and propose our DSQC schemes over the collective noise channel in Section 3 and Section 4, respectively. Then, in Section 5, we analyze the security of the proposed schemes. Finally, in Section 6, we summarize the work and give the main conclusion.
In this section, the elementary models of collective noise and DF subspace are first introduced. Then, the logical Bell states immune to collective-dephasing noise and collective-rotation noise are further defined, respectively.
The transformation of collective noise can be described by a unitary operation U(t), where t denotes the transmission time and means a temporal dependence. As mentioned in Ref. [32], if several photons transmit through the noisy channel and the time delay between them is small compared to τ fluc, the effect of collective noise on an N-qubit quantum state can be well approximated as the following model
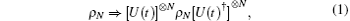
where τ fluc is the shortest time scale of thermal and mechanical fluctuations of the fiber, ρ N is a quantum state composed of N qubits, and [U(t)]⊗ N= U(t)⊗ · · · ⊗ U(t) denotes the tensor product of N unitary transformation operations U(t).
The collective noise is divided into two main types: the collective-dephasing noise and the collective-rotation noise. Therefore, when a polarized photon state | 0〉 (horizontal polarization state) or | 1〉 (vertical polarization state) passes through the noisy channel, it will experience the transformations of the collective-dephasing noise and the collective-rotation noise, which can be formulized as follows according to Eq. (1), respectively.[33]
(i) A collective-dephasing noise can be described as
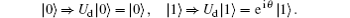
(ii) A collective-rotation noise can be described as
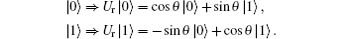
Here,
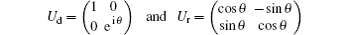
indicate the equivalent unitary operations of the collectivedephasing noise and the collective-rotation noise respectively, and θ is the parameter of the noise fluctuating with time.
The DF subspace is invariant under collective noise no matter how strong the interaction is, which can be modeled as

Due to the invariance property, the transmitted information is always carried by DF subspace in quantum communication. The amount of quantum information that a given DF subspace is able to protect is determined by the number of N qubits used.[60] Here, the elementary model of DF subspace for N = 2 is introduced as follows.
To combat the collective-dephasing noise, two basic logical qubits can be constructed as | 0dL〉 = | 0〉 1⊗ | 1〉 2 = | 01〉 12 and | 1dL〉 = | 1〉 1⊗ | 0〉 2= | 10〉 12, respectively. Here, the subscript “ 1” and “ 2” indicate two physical qubits, and “ dL” denotes the logical qubit immune to collective-dephasing noise.
Therefore, for N = 2, the DF subspace spanned by | 0dL〉 and | 1dL〉 can be generalized as
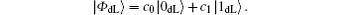
Here c0 and c1 are both complex numbers. In addition,
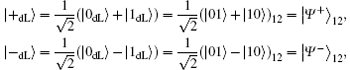
are another two common logical qubits resistant to collective-dephasing noise, in which | Ψ + 〉 12 and | Ψ – 〉 12 are two antiparallel Bell states from {| Φ + 〉 , | Φ – 〉 , | Ψ + 〉 , | Ψ – 〉 } .
Similarly, to counteract the collective-rotation noise two basic logical qubits can be constructed as
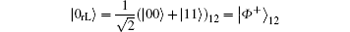
and
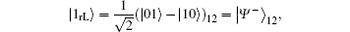
respectively. Accordingly, the generated DF subspace for N = 2 is that
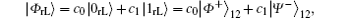
where, the subscript “ rL” denotes the logical qubit immune to collective-rotation noise. Obviously,
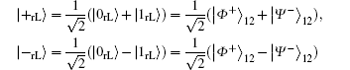
are another two common logical qubits immune to collective-rotation noise.
As explained in Ref. [60], the immunity of four-qubits polarization-entangled DF states against collective noise is experimentally verified by showing their invariance when passing the four photons through a noisy environment simulated by birefringent transmission medium. The special four-qubits DF states immune to collective noise, called logical Bell states, can be generated by using the product state of the aforementioned basic logical qubits, such as | 0dL〉 , | 1dL〉 , | + dL〉 , | – dL〉 .
To resist collective-dephasing noise, four logical Bell states denoted with 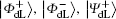

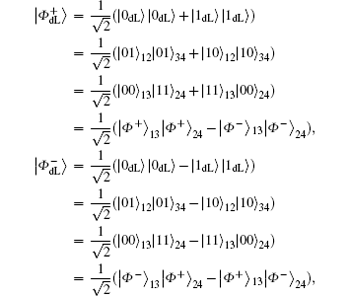
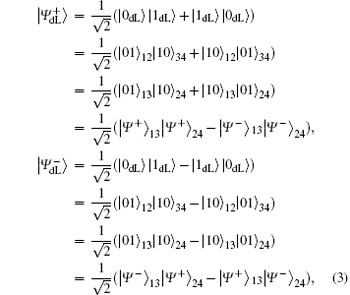
Obviously, the logical Bell states 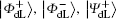
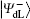
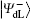
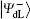
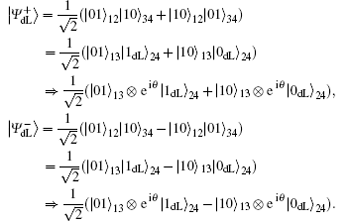
Here, eiθ is the global phase factor which is irrelevant to the observability of quantum states, and thus the actual fidelity of a quantum state can be regarded as 1 when it experiences the quantum collective-dephasing noise channel.
With the similar means as stated in Subsection 2.2, the corresponding logical Bell states immune to collective-rotation noise, denoted with 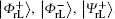
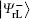

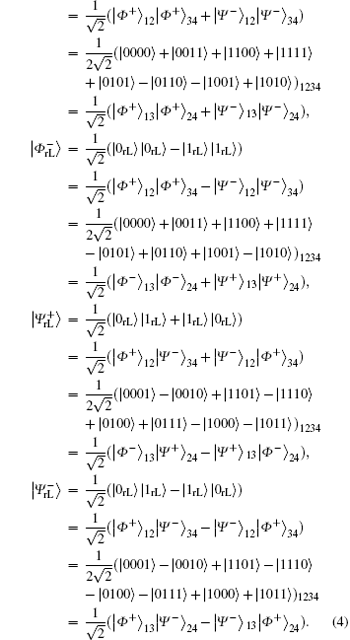
Undoubtedly, the generated four logical Bell states 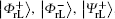
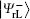
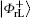
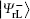
In this section, two novel coding functions are constructed in detail. The coding function for the logical Bell states immune to collective-dephasing noise is introduced in Subsection 3.1, and the other one for the logical Bell states immune to collective-rotation noise is proposed in Subsection 3.2. In either coding function, the specific unitary operations are utilized to encode the classical secret message, and the Bell measurements are used to decode the corresponding secret message.
In this subsection, the coding function, including encoding function and decoding function, is constructed over the collective-dephasing noise channel as follows.
It is not difficult to find that there is a specific property among the four logical Bell states immune to collective-dephasing noise according to Eq. (3). That is, 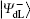
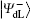
In the encoding function, two unitary operations U0 and U1 are introduced to encode a one-bit classical message “ 0” and “ 1” , respectively, where U0= I = | 0〉 〈 0| + | 1〉 〈 1| , U1= σ z= | 0〉 〈 0| − | 1〉 〈 1| . Here, we take 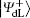
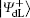
For encoding one classical bit “ 0” ,
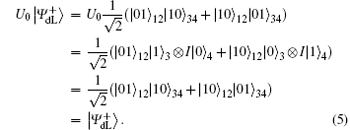
For encoding one classical bit “ 1” ,
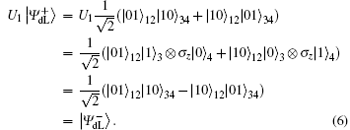
From Eq. (5) and Eq. (6), we can find that the final encoded states will be 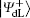
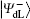
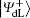
For the encoded state carried classical bit “ 0”
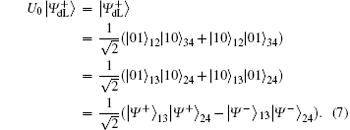
For the encoded state carried classical bit “ 1” ,
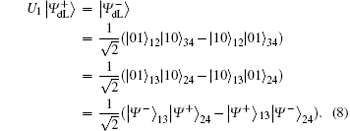
Based on the joint correlations of the Bell measurement results, a decoding table can be constructed as shown in Table 1, which shows the correspondence of the unitary operation, Alice's Bell measurement result (ABMR) on the 1st and the 3rd qubits, Bob's Bell measurement result (BBMR) on the 2nd and the 4th qubits, and the transmitted secret message over the collective-dephasing noise channel in detail.
| Table 1. The decoding table against collective-dephasing noise. |
This subsection introduces the coding function, i.e., encoding function and decoding function, against collective-rotation noise as follows.
Similar to Subsubsection 3.1.1, the encoding function can be constructed by performing the corresponding unitary operation on the 4th qubit in 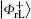
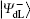
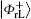
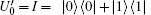
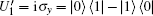


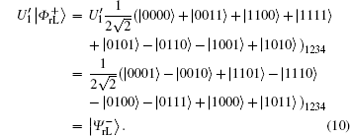
Similar to Subsubsection 3.1.2, if the corresponding Bell measurements are performed on the 1st and the 3rd qubits, and the 2nd and the 4th qubits in 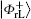
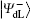
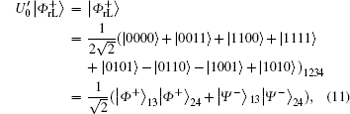
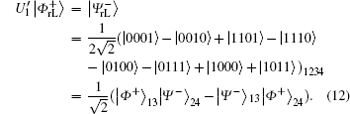
Correspondingly, the decoding table of the logical Bell states immune to collective-rotation noise can be constructed as the following Table 2.
| Table 2. The decoding table against collective-rotation noise. |
In this section, two DSQC schemes are presented. The DSQC scheme against collective-dephasing noise is constructed in Subsection 4.1, and the DSQC scheme against collective-rotation noise is constructed in Subsection 4.2.
In the proposed DSQC scheme, the two legitimate users are supposed to be the sender Alice and the receiver Bob, and n classical bits of secret message to be communicated between them are denoted with a sequence
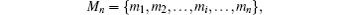
where mi ∈ {0, 1} with i= 1, 2, … , n. The main process of the DSQC scheme against collective-dephasing noise is demonstrated in the following steps.
Step 1 Initializing phase
Alice prepares n ordered logical Bell states all in 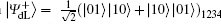
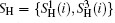
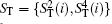
Step 2 Encoding phase
Alice encodes the secret message Mn to be communicated with Bob. That is, if the secret message mi is “ 0” (or “ 1” ), then Alice performs the unitary operation U0 = I = | 0〉 〈 0| + | 1〉 〈 1| (or U1 = σ z= | 0〉 〈 0| − | 1 〉 〈 1| ) on the 4th qubit in 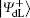
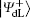
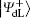
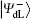
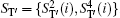
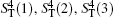
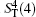
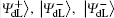
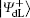
Step 3 Eavesdropping check phase
Alice randomly inserts the prepared l decoy logical qubits into ST′ to get ST* and send it to Bob via the quantum channel. Note that the transmitted states in the sequence 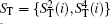
Step 4 Decoding phase
According to Eq. (7) and Eq. (8), Alice performs the Bell measurement on the particles in the sequence 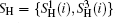
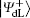
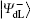
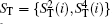
Alternatively, the process of the DSQC scheme against collective-rotation noise is similar to the DSQC scheme against collective-dephasing noise. There are a few differences listed as follows.
In the initial phase, Alice prepares the logical Bell state 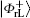
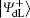
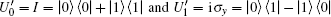
In this section, the security of the proposed scheme is further discussed including the security against an information leakage problem, an intercept-resend attack, an entangle-measure attack, a correlation– elicitation attack, and a Trojan horse attack. It should be noted that only the security analysis of the proposed scheme over the collective-dephasing noise channel is given in detail, which is suitable for the proposed scheme over the collective-rotation noise channel.
Information leakage is a common problem, that is, the malicious eavesdropper, Eve, can deduce partial or entire secret messages only by analyzing the transmitted qubits or classical bits between the sender Alice and the receiver Bob. For the proposed DSQC scheme against the collective-dephasing noise, the information leakage problem may occur in two cases.
The first case is that Eve intercepts the transmitted qubits, and measures them to extract the carried useful information. This case occurs before the eavesdropping check phase, so Eve may steal the secret message successfully without being detected. If so, even though the attack action is discovered by the subsequent eavesdropping check, it will be too late. However, this case cannot work well in the proposed DSQC scheme. As we know, after the unitary operation U0 = I= | 0〉 〈 0 | + | 1〉 〈 1| (or U1 = σ z= | 0〉 〈 0| − | 1〉 〈 1| ) is performed, a one-bit secret message “ 0” (or “ 1” ) is encoded on the corresponding qubits 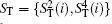

The second case is that Eve can wiretap the exchanged classical information in the decoding phase to attempt to distill Alice′ s secret message. Generally, this case always takes place after the eavesdropping check phase, so Eve will not be detected as long as she obtains the transmitted secret message in this situation. However, Eve also has no chance to achieve this aim in the proposed DSQC scheme. When Eve captures the exchanged classical bit “ 0” (or “ 1” ), she can easily infer Alice′ s measurement result on the corresponding qubits 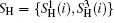
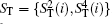
The intercept-resend attack always works well on many quantum secure communication schemes.[64– 66] Suppose the intercept-resend attack is carried out on the proposed DSQC scheme. In the eavesdropping check phase, Alice randomly inserts l decoy logical qubits from {| 0dL〉 , | 1dL〉 , | + dL〉 , | – dL〉 } into ST′ to guarantee the security of the quantum channel between Alice and Bob. Similar to the famous BB84 protocol, the probability for the eavesdropper to pass the public discussion for one decoy logical qubit is 3/4 without knowing the corresponding information of the position and the measurement basis in advance. Accordingly, the probability of avoiding the eavesdropping check successfully for the eavesdropper for all l decoy logical qubits is (3/4)l, which will converge to zero as l is large enough. Therefore, suppose a potential eavesdropper, Eve, intercepted the sequence ST* to measure it, and then resent a forged sequence to Bob, she would be detected inevitably in this step.
The entangle-measure attack[69, 70] should be considered in the presented DSQC scheme. In this attack, the eavesdropper prepares some specific particles in advance and entangles them with the sent sequence. By measuring these particles, the eavesdropper may obtain the information about the encoding operations and further deduce the secret message. Suppose that Eve prepares n+ l auxiliary logical qubits, PdL= {| PdL(i)〉 } for i= 1, 2, … , n+ l. According to Stinespring dilation theorem, Eve can entangle | PdL(i)〉 with the corresponding qubits | ST*(i)〉 by a unitary operation Ê on a larger Hilbert space when Alice sends ST* to Bob in Step 3, that is, Ê | ST*(i), PdL(i)〉 = Ê | ST*(i)〉 | PdL(i)〉 . However, since the quantum states of the decoy logical qubits are unknown to Eve, there will be four possible outcomes after performing the unitary operations on each decoy logical qubits as follows:
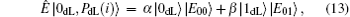
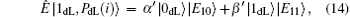
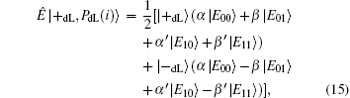
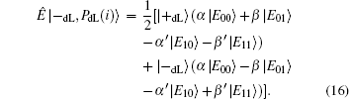
Here, since Ê is a unitary operation, the complex number α , β and α ′ , β ′ must satisfy
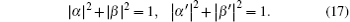
Hence, if Eve wants to pass the eavesdropping check and derives the useful information from the encoding operations, the following relationships should be established. Here, | E00〉 , | E01〉 , | E10〉 , and | E11〉 are four quantum states which can be distinguished by Eve.
i) From Eq. (13), the complex number β should satisfy β = 0 when the decoy logical qubits is | 0dL〉 .
ii) From Eq. (14), the complex number α ′ should satisfy α ′ = 0 when the decoy logical qubits is | 1dL〉 .
iii) From Eq. (15), the mathematical relation α | E00〉 − β | E01〉 + α ′ | E10〉 − β ′ | E11 〉 = 0 should hold when the decoy logical qubits is | + dL〉 , where 0 is represented as a zero vector.
iv) From Eq. (16), the mathematical relation α | E00〉 + β | E01〉 − α ′ | E10〉 − β ′ | E11 〉 = 0 should hold when the decoy logical qubits is | – dL〉 , where 0 is represented as a zero vector.
Therefore, only when the four relationships above are all satisfied synchronously, can Eve′ s attack not be detected during the public discussion of the eavesdropping check. Consequently, the equation that α | E00〉 − β ′ | E11〉 = 0 is established as the equation that β = α ′ = 0 holds, which indicates that α | E00〉 = β ′ | E11〉 . That is, Eve cannot distinguish | E00〉 from | E11〉 , which is contradictory to the precondition. Conversely, if Eve tries to make them distinguishable, i.e., α | E00〉 ne β ′ | E11〉 , to obtain some useful information, the decoy logical qubits will be inevitably disturbed, and Eve will be certainly detected. Therefore, Eve will not obtain any secret message if she launches the entangle-measure attack on the proposed DSQC scheme.
In the correlation– elicitation (CE) attack, [69, 70] the eavesdropper can distill part or all of the secret message by utilizing the relationship between two different qubits at different times. Performing CNOT operations on the particles introduced by an eavesdropper and the particles transmitted between the legitimate users is the usual means to implement this attack. Suppose that Eve performs the CE attack on the proposed DSQC scheme. As we know, the attack will be successful if Eve can deduce Bob′ s Bell measurement results on 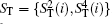
Herein, to illustrate this attack explicitly, we take | E〉 = | 00〉 as an example. In fact, the following analysis is analogical whenever the quantum state | E〉 is a single particle polarization state or a multi-particle entangled state. Then, in Step iii), Eve intercepts the sequence ST* and perform the CNOT operations, in which the particles in ST* are the control qubits while the corresponding particles in SE* are the target qubits, to generate the six-qubits entangled states. Subsequently, she resends the sequence ST* to Bob as usual, while keeping SE* in her quantum register. Once she gets the information about the position and measurement basis of the decoy logical qubits in Step iii), Eve immediately performs the corresponding Bell measurements on the particles in SE* to deduce Bob′ s measurement outcomes according to the joint correlations of the Bell measurement results in the six-particle entangled states. Then, she further wiretaps Alice′ s Bell measurement results to attempt to reveal the secret message in Step iv). Even so, the CE attack also will be detected eventually, since the decoy logical states | 0dL〉 , | 1dL〉 , | + dL 〉 , and | – dL〉 will be transformed into the corresponding quantum states after the CNOT operations, respectively.
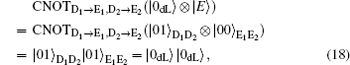
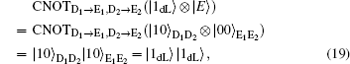
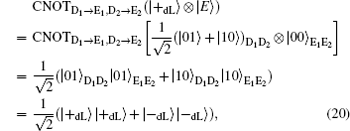
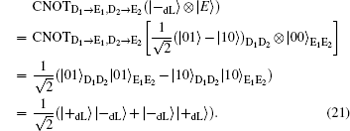
Here, the qubits denoted with the subscripts “ D1” and “ D2” , are the control qubits in decoy logical states, and the corresponding qubits denoted with the subscripts “ E1” and “ E2” , are the target qubits in SE*. Obviously, according to Eq. (18) and Eq. (19), Eve can avoid the eavesdropping check successfully when the decoy logical is | 0dL〉 or | 1dL〉 . However, she will be detected with the probability of 1/2 when the decoy particle is | + dL〉 or | – dL〉 according to Eq. (20) and Eq. (21). So, the total probability of being detected by the eavesdropping check is 1 − (3/4)l for l decoy logical qubit, which approaches to 100% as l is large enough. Therefore, the proposed DSQC scheme is security against the CE attack.
Plenty of quantum secure communication protocols easily suffer from Trojan horse attacks, i.e., the invisible photon eavesdropping (IPE) attack and the delay-photon attack.[71, 72] In an IPE attack, the eavesdropper produces an invisible spy photon sequence whose wavelength is close to the legitimate one, and adds it to the sent sequence. In a delay-photon attack, the eavesdropper inserts a spy photon sequence into a legitimate signal with a delay time, shorter than the time windows. The attacker can capture these spy photons and deduce the secret message by performing an appropriate measurement.
In the proposed DSQC scheme, Eve may try to get the secret message by carrying out the IPE attack. That is, she produces a special photon sequence SE* composed of n+ l Bell states from {| Φ + 〉 , | Φ – 〉 , | Ψ + 〉 , | Ψ – 〉 } with the wavelength λ ′ ≈ λ , where λ is the legitimate wavelength. Then, in Step iii), she inserts SE* into the transmitted sequence ST* and forwards them to Bob. Generally speaking, only when the legitimate sequence is transmitted at least twice, may the eavesdropper have the opportunity to deduce the secret message by analyzing the measurement results of the spy photon sequence. However, in the proposed DSQC scheme, the sequence ST* is only transmitted one way, i.e., from Alice to Bob, so that Eve has no chance to filter out the inserted invisible photons and measure them to steal the secret message. Moreover, the unitary operations have been performed by Alice before the spy photon sequence is inserted, and Bob only performs the corresponding measurement without any unitary operations for decoding the secret message. Therefore, the eavesdropper Eve still cannot reveal the secret message even though she captures the spy photon sequence. Similarly, when the delay-photon attack is carried out, Eve also cannot obtain any useful secret information. Therefore, Trojan horse attacks can be congenitally avoided without introducing extra hardware devices, such as the wavelength filter and photon number splitter (PNS).
To summarize, our paper proposes two DSQC schemes using logical Bell states, which are resistant to one kind of collective noise: the collective-dephasing noise and the collective-rotation noise, respectively. Compared with other DSQC schemes, [56– 59] our proposed scheme has two merits. The first one is that the logical Bell states (i.e., the four-particle decoherence-free states) are exploited to design the DSQC scheme for the first time. In order to implement the transmission of the secret message, two novel coding functions are constructed by advantage of the property of the logical Bell states. Based on the new coding functions, the sender, Alice, can encode her secret message by two simple unitary operations and the receiver, Bob, can read out the secret message by merely using the Bell measurements after the additional classical information is exchanged. For simplicity, we demonstrate the process of the proposed DSQC scheme over the collective-dephasing noise channel in detail against over collective noise. The second one is that the technique of decoy logical qubits checking and the strategy of one-step quanta transmission are combined together in our DSQC scheme. This combination not only ensures the security of the communication between two legitimate users, but also effectively reduces the influence of other noise existing in the quantum channel. The final security analysis shows that both the proposed DSQC schemes are feasible and robust against the information leakage attack, the intercept-resend attack, the entangle-measure attack, the correlation– elicitation attack, and the Trojan horse attack over the collective noise channel.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|
| 72 |
|