The continuous variable (CV) entanglement light has been an interesting research subject theoretically and experimentally, as it could be used as a basic resource for this new type of information processing.^[1] The experimental achievements include demonstrations of quantum teleportation, ^[2] quantum dense coding, ^[3] and quantum cryptographic communication^[4] by using the squeezed light. The bipartite CV entanglement states of a light field were studied in Refs.  [5] and [6] and demonstrated experimentally^[7] for a non-degenerate optical parametric amplifier (NOPA). The production of tripartite CV entangled beams by mixing squeezed states with linear optical elements can be found in Refs.  [8]– [13]. The genuine four-partite CV entanglement has been experimentally generated.^[14] Pfister et al. 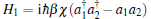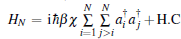proposed multipartite CV entanglement from concurrent nonlinearities through the generalization of bipartite interaction Hamiltonian to N-partite interaction Hamiltonian .^[15] Based on previous work, ^[16] we derive the generalized V₁ criterion for multipartite entanglement.^[17]

At present, the squeezing and entanglement of pulse frequency combs have attracted a great deal of attention because of their potential applications in quantum communication. The dispersion is one of the critical factors. In order to avoid the dispersion effect, the interaction lengths may be restricted to being very short, which limits the degree of squeezing.^{[18– 21]} Takahashi et al. investigated the effects of dispersion on both quadrature squeezing and photon statistics by varying the interaction length when pumping a PPLN crystal with fs pulses.^[22] We studied the phase mismatched phenomenon resulting from the dispersion effect, by periodically changing the polarity of crystal to obtain the optimal squeezing condition, and obtained the characteristic of EPR entanglements.^[23] In this paper, we discuss the influence of the dispersion effect, find the solution of the time-dependent FPE with the dispersion, and investigate the entanglement characteristics for N = 2– 5 partite. The investigation is especially important for the pulse OPO and the quantum characteristics of pulse frequency combs.

The Hamiltonian describing this system for multipartite entanglement is

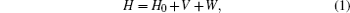
where

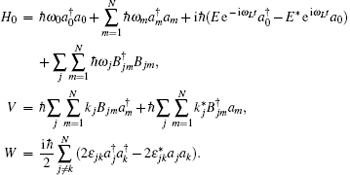
According to the non-degenerate mode operators b₁, … , b_N obtained by Ref.  [17] and the standard technique, ^[24] we define α _j = 〈 b_j〉 , j = 1 ∼ N, α ₀ = 〈 a₀ 〉 . Assuming the dynamic equation to have the initial values α ₁₀ = α ₂₀ = · · · = α _N0 = 1, α ₀₀ = 0, we have α ₁ = α ₂ = · · · = α _N . Considering the interaction between the medium and the optical field, we have the nonlinear susceptibility χ = χ ′ + iχ ″ , where χ ′ is the revised refractive index, χ ″ is the gain, the dispersion effect is neglected, and only the imaginary part χ ″ is retained. The semi-classical equations describing the interactions between pump wave α ₀ (τ ) and parametric waves α ₁ (τ ), α ₂ (τ ) become^[25]

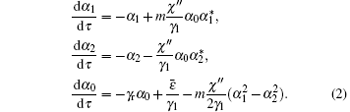
Here τ = γ ₁t is the dimensionless time, γ ₁ and γ ₂ are the damping rates, and decay ratio γ _r = γ ₂/γ ₁, 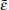is the amplitude of external coherent field, and m = N − 1 is the number of particles.

Considering the influence of dispersion,

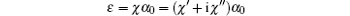
is the dielectric coefficient, the refractive index of the nonlinear susceptibility is

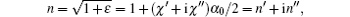
the real part n′ denotes the revised refractive index when the light with different frequencies passes through a medium, whereas the imaginary part n″ denotes the gain.^[23] When α ₁ = α ₂, in terms of Eq.  (2), the semi-classical equation for the DOPA system becomes

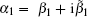
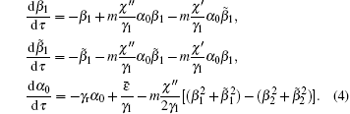
Assuming α ₀ to be real and writing the complex α ₁ as containing real and imaginary parts, equation  (3) turns into

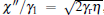
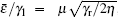
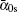
We take the parameters and assume the dispersion factor σ = χ ′ χ ″ = 0.5, the numerical solutions of α ₀, and β ₁ with γ _r = 0.5, η = 1/1000, and μ = 2 are depicted in Fig.  1.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Relations among the pump wave α 0 (solid line), steady state value of the pump wave (straight line), and the parameter wave β 1 (dashed line) for σ = 0, 1, N = 2– 5 respectively.

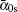
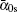
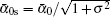
Figures  1(a) and 1(b) describe the relations among pump wave α ₀, steady state value of the pump wave, and parameter wave β ₁ for σ = 0, 1, N = 2– 5, respectively. Considering the effect of dispersion, the straight line corresponds to steady state value , the solid line corresponds to pump wave α ₀, and the dashed line corresponds to parameter wave β ₁ . Comparing Fig.  1(b) with Fig.  1(a), we have , where denotes the steady state value of the pump wave without dispersion. The squeezing curve contracts to the left, nearly equals 1/(1 + μ ).

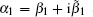
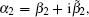
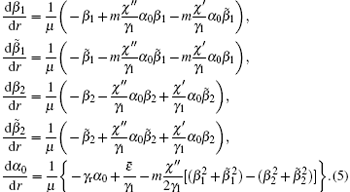
Considering the effect of dispersion, according to Eq.  (2), the complex , and the semi-classical equations for the NOPA system turn into^[26]

Considering the initial condition , α ₀₀ = 0, the numerical solutions of Eq.  (5) yield the dependences of the parametric functions α ₁, α ₂ on the squeezing parameter r

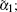
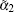
The quantum fluctuation of the time-dependent linearly driven NOPA system is^[27]

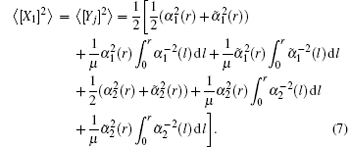
The correlation between X₁ and Y₂ is

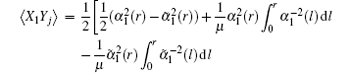
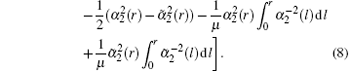
The variance criterion V₁ is^[23]

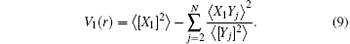
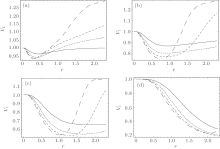
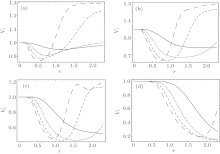
In the following, we investigate the influence of dispersion on multipartite entanglement. (i) μ = 0.5 for below-threshold, (ii) μ = 1 for the threshold, (iii) μ = 2 for the above-threshold, and (iv) μ = 10 for far-above-threshold. The results of numerical calculation of V₁ versus r with η = 1/1000 and γ _r = 10 for N = 2– 5 are depicted in Figs.  2 and 3.

Figures  2 and 3 depict the minimum variance V₁ as a function of squeezing parameter r = μ τ for σ = 0, 1, respectively. From bottom to top, the plots are for bipartite entanglement (N = 2, solid curve), tripartite entanglement (N = 3, narrow dashed curve), four-particle entanglement (N = 4, wide dashed curve), and five-particle entanglement (N = 5, dashed– dotted curve). Given dispersion factor σ , with the increase of pump parameter μ , the value of minimum variance V₁ decreases. Comparing Fig.  3 with Fig.  2, the scope of entanglement decreases from 10 to 2. The phase increases with the increase of pump parameter μ , namely φ = μ r = 10 × 1.5 ≈ 5π , the polarity of gain medium changes many times, the net gain descends as shown in Figs.  2 and 3.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Plots of variance V1 versus τ with σ = 0, μ = 0.5 (a), μ = 1 (b), μ = 2 (c), μ = 10 (d).

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Plots of variance V1 versus τ with σ = 1, μ = 0.5 (a), μ = 1 (b), μ = 2 (c), and μ = 10 (d).

In this paper, we investigate the multipartite entanglement of FNOPA system with considering the effect of dispersion, the results are as shown in Figs.  1– 3. The nonlinear interaction becomes strong due to dispersion coefficient σ . With the increase of pump parameter μ , the minimum variance V₁ decreases. The minimum variance V₁ decreases with the increase of the number N of particles.