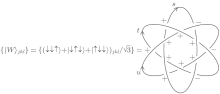Because of the very importance of quantum entanglement^{[1– 13]} we try to find the connection between entangled states and oriented links in knot theory, ^{[14– 16]} and have successfully found such deep connections.^{[17– 31]} Recently, based on our previous works about the correspondence between four Bell bases and four oriented links 4₁ in knot theory, ^{[17, 18]} and the correspondence of eight GHZ quantum entangled states and eight oriented links 12₁ in knot theory, ^[19] furthermore, we have shown that there exists a very simple and vivid way of obtaining the linkage 4₁ by using the method of torus knot theory.^[30] Firstly we find the knotted picture of Bell bases (number of qubits m = 2) on the surface of trivial torus, the torus link K_{4, 2}, then after quitting the trivial torus and projecting the torus link on a plane, we can easily obtain the knotted pictures of Bell bases, the linkage 4₁. Similarly on the ordinary plane, ^[30] we find the knotted picture of eight GHZ quantum states (number of qubits m = 3) on the surface of trivial torus, the torus link K_{6, 3}, then after quitting the trivial torus and projecting the torus link on a plane, we can easily obtain the knotted pictures of eight entangled GHZ quantum states, and the linkage 12₁, on the ordinary plane.^[31] In general, for m qubits GHZ states we have shown that the knotted picture of 2^m oriented links can be represented by the torus link K_{2m, m} on the surface of trivial torus.^[31] From all our research about the relationship between entangled states and oriented links we can confidently draw the following conclusions: there exists the correspondence between entangled quantum states and oriented links in knot theory; every qubit corresponds to its own knot in the oriented link corresponding to the given entangled state; this correspondence can be used to predict some new undiscovered entangled states and related phenomena.

However, all our previous research was limited to generalized GHZ states; however, in 2000 the authors in Ref.  [12] pointed out that there are two fundamental types of entangled quantum states, the GHZ states and W states for 3-node quantum entangled states. So, what kinds of oriented links correspond to the W states? This paper aims at solving this problem. From the method of discovery of the correspondence between four Bell bases and four oriented links of the linkage 4₁ in knot theory, ^{[14– 16]} we already know that, on the one hand, we must find the covariance correlation tensor (CCT) in the theory of quantum network for the W states, on the other hand, we should find the Alexander relation matrix (ARM) in the theory of knot crystals for the W states, then by the comparison of obtained results, we can confirm the exactness of the correspondence between W states and their corresponding knotted pictures.

The organization of this paper is arranged as follows. In Section 2 we are going to find the matrix of CCT of the degenerated 2-node W state from the theory of quantum networks. In Section 3 we shall conjecture another possible oriented link (which is composed of two component knots entangled with each other and has four crossings) as the knotted picture of the 2-node W state and find the nonzero submatrix of the ARM of the conjectured linkage from the theory of knot crystals. We find that the nonzero submatrix of the CCT exactly equals the nonzero submatrix of the ARM of the conjectured 2-node W state, thus confirming our conjecture about the knotted picture of 2-node W states. From the 3-node W states |W 〉 _jkl, we can obtain three different kinds of degenerated 2-node W states, which are |W 〉 _kl, |W 〉 _jl or |W 〉 _jk. Thus, when we have obtained their corresponding knotted pictures, the superposition of these knotted pictures will give the knotted pictures of 3-node W states. Hence the correspondence between quantum entangled states and oriented links in knot theory is also true for W states. Comparison of the knotted pictures of Bell bases (i.e. 2-node GHZ states) with those of the conjectured 2-node W states, we find that the latter pictures are just the results obtained by the application of the surgical operation flip in knot theory on the third crossing of the former pictures. This is the intimate and simple relationship between GHZ states and W states in knot theory.

Firstly we will give the definition of CCT for a quantum network of two nodes (m = 2). Quantum network^[13] is a system consisting of m subsystems (nodes) interacted with each other in n-dimensional Hilbert space. Let ν be the ordinal numbers of the nodes, s be the dimensionality of the generating operator of SU, where s = n² − 1. In the case of a single node, i.e. ν = 1 only, the density operator is:^[13]

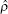
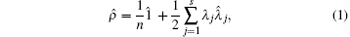
where λ _j is the expectation value of , i.e.

In the case n = 2, s = n² − 1 = 3, 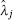is just the Pauli operator , ^{[13, 17]} whereas

In the case of two nodes, for example, ν = 2, 3, the density operator 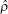is:^{[13, 17, 20, 21]}

where . The correlation tensor K_kl(2, 3) is defined as^{[13, 17, 20, 21]}

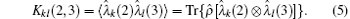
The CCT M_kl(2, 3) is introduced as^{[13, 17, 20, 21]}

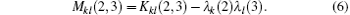
For a quantum network of three nodes, the density operator is given by Refs.  [13], [20], [21], and [22], for brevity we will not list this expression, here we only point out that equation  (4) can be directly obtained from by emptying the first node j, hereafter we shall use the symbols j, k, l to represent the quantities related to the first, the second, and the third nodes respectively, hence the density operators corresponding to three degenerated two-nodes quantum states can be directly obtained from by emptying j, k, l respectively.

Equation  (4) can be written as^{[13, 17, 20, 21]}

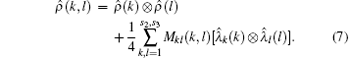
When M_kl(k, l) = 0 for all possible k and l, equation  (7) becomes the product state 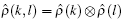, that is, there is no entanglement, i.e., no inter-node coherence. Hence the tensor M_kl(k, l) allows the term entanglement to be defined in a precise way. The criterion of the entangled state for a composite system consisting of two nodes is: M_kl(2, 3) is not equal to zero for all possible k and l, i.e., there is nonzero elements in CCT.

The value of a qubit is taken to be zero and one for | ↓ 〉 and | ↑ 〉 respectively. In the case of a system of two nodes m = 2, we know that there are four basic product states, which are |↓ ↓ 〉 = |00〉 = |1〉 , |↓ ↑ 〉 = |01〉 = |2〉 , |↑ ↓ 〉 = |10〉 = |3〉 and |↑ ↑ 〉 = |11〉 = |4〉 . From these four basic product states we construct four Bell bases, which are 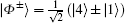and . In the case of three nodes (m = 3), we know that there are eight basic product states which are |↓ ↓ ↓ 〉 = |000〉 = |1〉 , |↓ ↓ ↑ 〉 = |001〉 = |2〉 , |↓ ↑ ↓ 〉 = |010〉 = |3〉 , |↓ ↑ ↑ 〉 = |011〉 = |4〉 , |↑ ↓ ↓ 〉 = |100〉 = |5〉 , |↑ ↓ ↑ 〉 = |101〉 = |6〉 , |↑ ↑ ↓ 〉 = |1, 1, 0〉 = |7〉 , and |↑ ↑ ↑ 〉 = |111〉 = |8〉 . Actually, Bell bases are GHZ (Greenberger– Horne– Zeilinger) states for m = 2. From these eight basic product states we can construct eight GHZ states for m = 3:

Dü r et al.^[12] pointed out that there are only two types of entangled states for a quantum network of three nodes: GHZ states and W states. The eight GHZ states are constructed from two basic product states for a quantum network of three nodes, as shown in Eq.  (8), whereas the eight W states (four quantum states 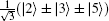and the other four quantum states ) are constructed from three basic product states for a quantum network of three nodes, for example .

In our two previous papers, ^{[17, 18]} we have discussed the correspondence between four Bell bases and the four oriented links of the linkage 4₁ in knot theory, ^{[14– 16]} and the correspondence between GHZ states and the oriented links of the linkage 12₁ in knot theory.^[19] Now we shall use the same method to find the correspondence of eight W states |W〉 _jkl and the eight expected oriented links in knot theory.

We already know that eight GHZ states |GHZ〉 _jkl will degenerate into four Bell bases under the condition that any one qubit disappears, hence |GHZ〉 _kl, |GHZ〉 _jl, and |GHZ〉 _jk all correspond to four Bell bases. Similarly, the eight W states |W〉 _jkl will degenerate into four unnamed degenerated entangled states under the condition that any one qubit disappears (i.e., |W〉 _kl, |W〉 _jl or |W〉 _jk). In this section we shall go to find the CCT M_kl of the unnamed degenerated entangled states |W〉 _kl. Without loss of generality, we choose one W state to calculate the correspoding matrix for the CCT of the degenerated W state |W〉 _kl. When we cancel the subscript j we readily obtain

The general expression of a pure state is^{[13, 21, 22]}

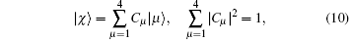
where | μ 〉 = | k 〉 ⊗ | l 〉 = | k, l〉 is a product state. The density operator of the pure state |χ 〉 is

where 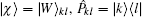are projection operators, the matrix elements ρ _kl are

The corresponding components of coherent vectors are

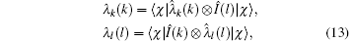
where the unit operator and generating operators are

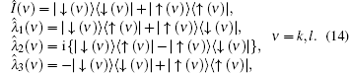
Substituting Eqs.  (9), (10), and (14) into Eq.  (13) we obtain

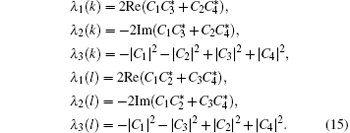
For degenerated W state |W〉 _kl,

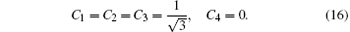
Using Eq.  (16), from Eq.  (15) we obtain

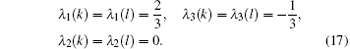
From Eqs.  (16), (17), (4), and (5) after a long and tedious calculation we obtain

Using the definition of CCT

we obtain the matrix of CCT for degenerated W state |W〉 _kl:

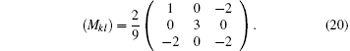
It is well known that in the case of 3-nodes (j, k, l), there are two types of quantum entangled states, the GHZ states and W states. We have already discovered the knotted pictures of GHZ states ({|GHZ〉 _jkl}).^{[19, 31]} When we empty any one node, then the obtained results {|GHZ〉 _kl}, {|GHZ〉 _jl}, {| GHZ_jk} are just the correponding knotted pictures of the Bell bases, which have the largest degree of entanglement of the linkage 4₁. The linkage 4₁ is a collection of two component knots, ^[17] it has four crossings when one component knot j (its ring parameter is s, for oriented knot, s⁺ and s⁻ denote the anticlockwise and clockwise directions of this knot respectively^[17]) crosses another component knot k (its ring parameter is t, for an oriented knot, t⁺ and t⁻ denote the anticlockwise and clockwise directions of this knot respectively^[17]). There are two types of crossing, one is over-crossing when j crosses over k, another is under-crossing when j crosses under k. We already know that the Bell bases correspond to the linkage 4₁ where over-crossing and under-crossing appear alternatively. When the two-component knots are still entangled with each other, then the only case for the distribution of four crossings for the linkage 4₁ is the case where one under-crossing followed by three over-crossings (or equivalently, one over-crossing followed by three under-crossings), whose degree of entanglement is apparently less than that corresponding to Bell bases. Now we will derive the ARM for this case, and find that the nonzero submatrix of the 4 × 4 ARM just equals Eq.  (20), thus we verify that this type of the linkage 4₁ is just the knotted picture of the required knotted picture {| W〉 _kl}, hence from the supperposition of {| W〉 _kl}, {| W〉 _jl}, {| W〉 _jk} we can readily obtain the knotted pictures of {| W〉 _jkl}.

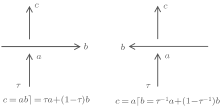
Now we empty the node j, and investigate the linkage 4₁ composed of two-component knots k and l (its ring parameter is u, for oriented knot, u⁺ and u⁻ denote the anticlockwise and clockwise directions of this knot respectively^[17]) in which one under-crossing is followed by three over-crossings. In Fig.  1 we give the supposed knotted picture, the directions of two-component knots are all chosen to be clockwise, O₁, O₂, O₃, and O₄ are four crossings, in which the first one is under-crossing, the others are over-crossings. Note that if we change O₃ from over-crossing to under-crossing, then figure  1 becomes the knotted picture of the Bell basis . Hence the conjectured link is intimately related with that of Bell basis.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. The supposed knotted picture of the quantum state | W〉 kl}, i.e., {| W〉 kl}.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Two modes of crossing.

There are two modes of crossings, the right cross b⌉ and the left cross ⌈ b, they will serve to encode the two oriented types of diagrammatic crossings as shown in Fig.  2.

As illustrated in Fig.  3, the incoming under-crossing arc is a, the emanating arc is c, the over-crossing arc is b, then we denote c = a b⌉ for the right cross, or c = a⌈ b for the left cross, here ab⌉ and a⌈ b are defined by the following equations

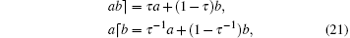
where a, b ∈ M, M is any module over the ring Z(τ , τ ^{− 1}), τ is the ring parameter. The ring parameters of the two-component knots are t and u for unoriented knots, and t⁺ , u⁺ or t⁻ , u⁻ for oriented knots with anticlockwise or clockwise direction respectively. The relations between these ring parameters are given by the following equations

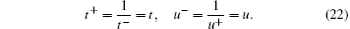
Now we shall use Eqs.  (21) and (22) to derive the ARM of the knotted picture shown in Fig.  1. From Fig.  1 we easily see that the arc y₂ emanating from the crossing O₁ is the same as the arc y₁ incoming into the crossing O₁, i.e., y₂ = y₁, hence y₂ = y₁z₁⌉ becomes y₁ = y₁z₁⌉ . Using Eq.  (21) for the four crossings and noting that y₂ = y₁, we get

Using Eq.  (22) to arrange Eq.  (23) we get%

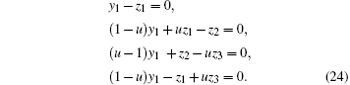
The coefficient matrix of the variables y₁, z₁, z₂, z₃ of Eq.  (24) is

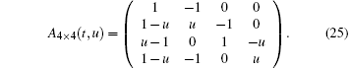
Using the method of a combination of rows and the method of a combination of coulumbs separately and repeatedly (see Appendix A), we can easily obtain

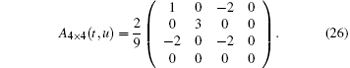
From Eq.  (26) we readily obtain the non-zero submatrix A_{3× 3}(t, u)

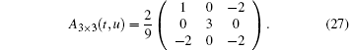
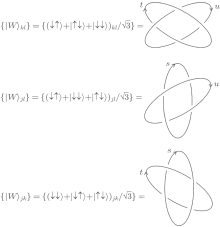
Thus we verify that the non-zero submatrix A_{3× 3}(t, u) exactly equals (M_kl), hence we can say that figure  1 is just the required knotted picture of the quantum entangled state | W〉 _kl, i.e., {| W〉 _kl}. Similarly we can easily find the knotted pictures corresponding to the cases when we empty the node k (i.e., {| W〉 _jl}) and the node l (i.e., {| W〉 _jk}) respectively. The knotted pictures of all these 2-node W states are given in Fig.  3.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The knotted pictures of 2-node W states: {| W〉 kl}, {| W〉 jl}, and {| W〉 jk}.

The superposition of all these 2-node W states readily gives the common 3-node W state as shown in Fig.  4.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The knotted picture of 3-node W state.

Note that oriented crossings in Fig.  4 are labelled with a plus or minus sign, when we can rotate the oriented over-crossing anticlockwise with an acute angle in order to coinside with the oriented under-crossing. The oriented crossing is called a positive crossing, if clockwise, then it is called a negative crossing. In Fig.  4, there are nine positive crossings and three negative crossings. In Fig.  1, crossings O₁, O₂, and O₄ are positive, whereas crossing O₃ is negative. In knot theory there is a surgical operation flip, ^[28] which changes the sign of the crossing, i.e. from positive to negative or from negative to positive, when we apply flip on crossing O₃, then O₃ becomes positive, then figure  1 becomes just the knotted picture of the Bell basis | Φ ⁻ 〉 .^[17] Furthermore, when we apply the flip on the right three negative crossings, then figure  4 becomes the knotted picture of one of the eight GHZ states.^{[19, 31]} Hence we can from the knotted pictures of GHZ states obtain those of W states just by the application of the surgical operation flip, or vice versa. This is the very important and very simple interrelations of the two fundamental types of the 3-node entangled quantum states: GHZ state and W state.