The magic wavelength is the wavelength at which the polarizability difference for a transition goes to zero; it means that the Stark shifts for the upper and lower levels of the transition are the same.^{[1– 4]} The magic wavelength is interesting^{[5– 9]} due to its importance in a number of applications. Especially, the magic wavelength has extensive applications in quantum state engineering and precision frequency metrology.^[10] The investigations of the magic wavelength open a new route to determine the line strength ratio, ^[11] and the measurements of the ratio of two line strengths can give the accurate transition matrix element, which is important in testing the reliability of models used to interpret atomic parity nonconservation (PNC) studies.^{[12, 13]} For an optical clock, a mageto-optical trap at the magic wavelength^{[14– 17]} can eliminate the ac Stark shift, which decreases the systematic uncertainties. A new generation of atomic clocks based on neutral atoms trapped in the magic-wavelength optical lattices^{[18– 21]} are under development.

The magic wavelength of a transition involving non-zero angular moment states not only connects with the dynamic dipole polarizability, ^{[3, 22– 24]} but also depends on the polarization direction of the linearly polarized laser. As for the linearly polarized laser, the dynamic dipole polarizability of the s (with angular moment L = 0) state in the laser field can be written as^[25]

where are the absorption oscillator strengths, ω is the laser frequency, and ɛ _gi is the excitation energy of the transition.

For the non-zero angular moment states, take the d (with angular moment L = 2) state of Ca⁺ for example, by using the linearly polarized laser, the dynamic dipole polarizability is given as^{[26, 27]}

where θ _p is the angle between the direction of polarization and the quantization z axis, and α _d(ω ) and are known as the scalar and the tensor dipole polarizabilities, respectively. When the laser is tuned to the magic wavelength, α _s(ω ) should equal α _d(ω , θ _p), in other words, for the s→ d transiton, the magic wavelength will change with angle θ _p. Furthermore, for two different atomic transitions involving four different energy levels, when the polarization of the linearly polarized laser is adjusted to a certain direction, the dynamic dipole polarizabilities of the four energy levels are equal at a certain wavelength, then the magic wavelength for the four states is determined.

In this paper, the magic wavelengths for different Zeeman transitions are measured based on the ⁴⁰Ca⁺ optical clock and the correlation between the magic wavelength and the polarization direction of the linearly polarized laser beam is studied. The result shows that two different atomic transitions have the same magic wavelength at a certain polarization direction when the linearly polarized laser is used. Furthermore, a pair of transitions was selected in the previous measurement of magic wavelengths for eliminating the difference caused by the component of the tensor polarizability. If a certain polarization direction of the linearly polarized laser is precisely chosen, the precision of the magic wavelengths can be improved within the same averaging time probing only one Zeeman transition.

For the 3d state of Ca⁺ , the two clock transitions corresponding to ❘ m❘ = 1/2, 4s_{1/2, m= 1/2} → 3d_{5/2, m= 1/2} and 4s_{1/2, m= − 1/2} → 3d_{− 5/2, m= − 1/2}, are shown in Fig.  1. According to the definition of the magic wavelength, the dynamic dipole polarizabilities of the two states are equal at the magic wavelength. If the two magic wavelengths are equal, then the dynamic dipole polarizabilities of the four relative states are the same, which will be shown in our expriement.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Partial energy level diagram of 40Ca+ .

A sketch of the experimental setup for studying the correlation between the magic wavelengths and the direction of the linear polarization of a 395  nm laser (L_m) is shown in Fig.  2. The whole system is composed of two main parts: the first one is an optical clock based on single trapped ⁴⁰Ca⁺ , the second one is the L_m laser system for measuring the light shift of the clock transition, in which the direction of polarization of the L_m laser can be precisely adjusted with a λ /2 plate and a Glan prism.

Fig.  2.

	Figure Option ViewDownloadNew Window
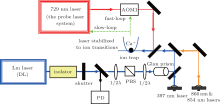	Fig.  2. Overview of the experimental setup. DL: diode laser; AOM: acousto-optic modulator; 1/2 λ : half wave plate; PD: photo diode; PBS: polarized beam splitter.

The optical clock system consists of a 729  nm narrow line-width laser, a single ion trapping system, and a closed-loop locking module, which has been described in previous work.^{[28– 31]} The 729  nm laser has a linewidth of less than 5  Hz, and the instability of the laser is 1 × 10^{− 14} for 20  s. For the ∼ 17  s feedback circle, the error due to the drift of the 729  nm probe laser for one measurement of the light shift of the clock transition can be smaller than 4  Hz, corresponding to ∼ 3  pm of the magic wavelength. The L_m laser is the key element in the measurement of the magic wavelength, so the L_m laser used in the experiment is frequency stabilized using a transfer cavity referenced to the 729  nm probe laser, and the long-term drift is reduced to less than 10  MHz within 4  h. An unpolarized beam splitter (BS) is used to split a part of the beam to a photodiode (PD) for monitoring the power of the L_m laser, which is also shown in Fig.  2. The waist radius of the beam is 203(5)  μ m, and the power of the beam is 731(4)  μ W. The other parameters of the L_m laser, such as the linear polarization purity and the jitter of the laser power, have been given in the previous paper.^[11]

In our experiment, a single ⁴⁰Ca⁺ ion is trapped in a miniature Paul trap, and the ion is cooled to a few mK by Doppler cooling. The single ion’ s excess micromotion is minimized with the RF-photon correlation technique.^[32] The clock transition splits into ten Zeeman components around the zero-field line center^[29] under an additional magnetic field. The magnetic field has an angle of ∼ 40° with the probe laser beam and ∼ 50° with the direction of the probe laser polarization. The probe laser is locked to the clock transition line of Ca⁺ by feeding back to the frequency of the acousto-optic modulator (AOM1) to compensate for changes from external factors. The pulse sequences of 397  nm, 866  nm, 854 nm, and 729 nm lasers are similar to those used in the ⁴⁰Ca⁺ ion optical frequency standard.^[29] The pulse sequence of the L_m laser is introduced to measure the light shift of the clock transition. The L_m laser is turned off during the Doppler cooling, and is on and off alternately during the probing stage to measure the light shift. The frequency of AOM1 is recorded automatically in every cycle by a computer, and the light shift caused by the L_m laser beam can be measured by calculating the difference of two cycles with the L_m laser on and off.

The L_m laser beam passes through a λ /2 plate and a Glan prism before going into the ion trap, thus we can adjust the polarization direction of the linearly polarized laser and maintain the purity of the linear polarization. The magic wavelengths for different Zeeman transitions were measured with a fixed polarization direction of the linearly polarized laser before studying the relationship between the magic wavelengths and the direction of the linear polarization. In the experiment, six transition lines were chosen, corresponding to m_j= ± 1/2, ± 3/2, ± 5/2 of the 3d_5/2 state. For each transition, the light shifts at several different fixed wavelengths around the magic wavelength were measured. The result shows that the light shifts for different atomic transitions at the same wavelength of the L_m laser are different, such as m_j = ± 1/2 of 3d_5/2 state, and the corresponding magic wavelengths obtained by linearly fitting the light shifts for different transitions are different, as shown in Fig.  3. As to ❘ m_j❘ = 3/2, 5/2 of the 3d_5/2 state, the same results were obtained.

Fig.  3.

Figure Option ViewDownloadNew Window

Fig.  3. The relationship between the magic wavelengths of transitions 4s1/2, m= ± 1/2 → 3d5/2, m± 1/2 and angle θ . The θ is the angle between the direction of the linear polarization and the vertical direction. The solid red circles and the solid black blocks represent the measured magic wavelengths at different angles, and the blue triangles are the average values. The errors indicated are the statistical errors of the measurements. The black line in the insert is the average of six blue triangles, and the dashed lines indicate the statistical uncertainty.

Finally, the two atomic transitions corresponding to ❘ m_j❘ = 1/2 were chosen to study the correlation between the magic wavelengths and the direction of the linear polarization experimentally. In the experiment, the reference direction is chose as the vertical direction, and θ is the angle between the polarization direction of the L_m laser and the reference direction. In addition, the clockwise direction is defined as positive. Six different angles were chosen in a range of 50° . The magic wavelengths λ _{mj= 1/2} of clock transition 4s_{1/2, m= 1/2} → 3d_{5/2, m= 1/2} and λ _{mj= − 1/2} of clock transition 4s_{1/2, m= − 1/2} → 3d_{− 5/2, m= − 1/2} at each angle were measured respectively, as shown in Fig.  3. The solid red circles indicate the magic wavelengths of clock transition 4s_{1/2, m= 1/2} → 3d_{5/2, m= 1/2} at different angles, and the solid black blocks represent those of 4s_{1/2, m= − 1/2} → 3d_{− 5/2, m= − 1/2}. By analyzing the experimental data, it is found that there is a certain angle θ at which λ _{mj= 1/2} equals to λ _{mj= − 1/2}. In theory, the two magic wavelengths corresponding to transitions 4s_{1/2, m= 1/2} → 3d_{5/2, m= 1/2} and 4s_{1/2, m= − 1/2} → 3d_{− 5/2, m= − 1/2} will be equal when θ _p is adjusted to a certain value. In other words, the four energy levels of two different transitions have identical dynamic dipole polarizability with certain θ _p. The angle θ _p has a direct correlation with θ , and θ _p will change with θ , so there may be a θ in theory at which λ _{mj= 1/2} equals to λ _{mj= − 1/2}, which explains our finding.

As shown in Fig.  3, the blue triangles represent the average λ _{❘ mj❘ = 1/2} of two magic wavelengths λ _{mj= 1/2} and λ _{mj= − 1/2}. Here λ _{❘ mj❘ = 1/2} is constant with different angles of the linear polarization, it proves that the previous measurement^[11] of the magic wavelength is correct. Moreover, we can conclude that if the direction of the linear polarization is controlled precisely and the angle is adjusted to a certain value at which the two magic wavelengths are equal, λ _{❘ mj❘ = 1/2} can be obtained by measuring the magic wavelength of a single transition. This means that only one transition peak needs to be locked instead of two in the optical frequency standard, so the measurement precision of the magic wavelengths may be improved compared to the previous measurement.

Based on the measurement of magic wavelengths of different transitions corresponding to m_j= ± 1/2 of the 3d_5/2 state in ⁴⁰Ca⁺ , it is shown that the magic wavelengths for different atomic transitions at a fixed polarization direction of the linearly polarized laser are different. For the two clock transitions from the ground state to m_j= ± 1/2 of the 3d_5/2 state, we preliminary study the correlation between the magic wavelengths and the polarization angle of the linearly polarized laser. After the measurement of the magic wavelengths at different polarization directions of the linearly polarized laser, an angle at which the two magic wavelengths are equal is determined; there the four relevant states have equal dynamic dipole polarizability. In addition, the determination of the angle could give an innovative idea for improvement on the measurement precision of magic wavelengths and the measurement scheme is also suitable for ❘ m_j❘ = 3/2, 5/2 of the 3d_5/2 state.