†Corresponding author. E-mail: xietingx@djtu.edu.cn
‡Corresponding author. E-mail: shi ying@jlu.edu.cn
*Project supported by the Jilin University, China (Grant No. 419080106440), the Chinese National Fusion Project for the International Thermonuclear Experimental Reactor (ITER) (Grant No. 2010GB104003), and the National Natural Science Foundation of China (Grant No. 10974069).
A quasi-classical trajectory (QCT) calculation is used to investigate the vector and scalar properties of the D + BrO → DBr + O reaction based on an ab initio potential energy surface (X1A’ state) with collision energy ranging from 0.1 kcal/mol to 6 kcal/mol. The reaction probability, the cross section, and the rate constant are studied. The probability and the cross section show decreasing behaviors as the collision energy increases. The distribution of the rate constant indicates that the reaction favorably occurs in a relatively low-temperature region ( T<100 K). Meanwhile, three product angular distributions P( θr), P( ϕr), and P( θr, ϕr) are presented, which reflect the positive effect on the rotational angular momentum j’ polarization of the DBr product molecule. In addition, two of the polarization-dependent generalized differential cross sections (PDDCSs), PDDCS00 and PDDCS20, are computed as well. Our results demonstrate that both vector and scalar properties have strong energy dependence.
In recent decades, the A+ BC→ AB+ C system has been paid a great deal of attention for its superiority in dealing with the stereodynamics, which characterizes the reagent and product molecular collisions.[1– 10] As a prototype, the O + HBr and its isotopic variant reaction O+ DBr have attracted considerable attention.[11– 16] By employing a flow tube method, Brown et al.[17] determined the rate constants of the O + HBr → OH + Br reaction with temperature ranging from 267 K to 430 K. In 1988, McKendrick et al.[18] detected the OH product ro-vibrational state distributions by means of the laser-photolysis, which was consistent with the previous literatures. Later, the crossed molecular beam technique was applied to obtain the angular distributions.[19]
Meanwhile, the HOBr system has also become a benchmark of insertion reactions, barrierless with a deep well on its potential energy surface (PES). In 2000, a global ab initio PES for the X1A’ state was constructed by Peterson[20] using correlated multireference configuration interaction (MRCI) calculations. As mentioned above, the resulting HOBr PES is barrierless with a deep well which causes a long-lived intermediate compound. Tang et al.[21] calculated the rate constants of the O + HBr → OH + Br reaction by using the quantum mechanical (QM) method, which has gained sensitive results with the temperature. As its isotopic variant reaction, the O + DBr → OD + Br reaction has also been investigated in theory. In 2012, Li et al.[15] reported a quasi-classical trajectory (QCT) study on the product polarization of the O+ DBr reaction and concluded that the product polarization was affected by the mass combination and the deep well PES.
Thus far, their reverse reactions H+ BrO and D+ BrO have rarely been studied, while they are helpful to obtain the reaction mechanisms.[22] In order to explore the reaction dynamics and mechanism, in this work, the collision energy effect on the D + BrO → DBr + O reaction is investigated. Scalar properties such as reaction probability, cross section, and rate constant are calculated by the QCT method. Moreover, vector properties including P(θ r), P(ϕ r), and polarization-dependent generalized differential cross sections (PDDCSs) are also studied.
The ab initio potential energy surface obtained by Peterson[20] using the multi-reference configuration interaction method is employed in the present work. His computing results have achieved the spectral accuracy. Moreover, a deep potential well has been found in the entrance channel of the title reaction.
The QCT method adopted in this paper is similar to that described in the previous literatures.[23– 28] In our QCT calculations, the classical Hamilton equations are integrated numerically in three dimensions. Meanwhile, for each trajectory, the numerical integration accuracy is verified by checking the conservations of the total energy and the total angular momentum. In this paper, the collision energy is chosen to be 0.1– 6 kcal/mol and batches of 100000 trajectories are run for each collision energy. The trajectories are initiated at a distance of 10 Å between the D atom and the BrO diatom, and the integration step size is 0.1 fs.
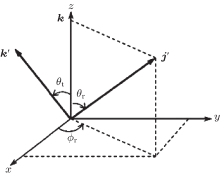
We employ the center-of-mass (CM) frame to investigate the angular distributions, which is displayed in Fig. 1.[29] The reagent initial relative velocity vector k is parallel to the z axis, and k and the final product relative vector k’ are in the scattering plane x– z. The angle θ t between k and k’ is the so-called scattering angle. The θ r and ϕ r are the polar and azimuthal angles of the rotational angular momentum vector j’ , which describe the vector correlations. The CM angular distributions and the scalar properties calculated in this work are partly displayed in the following; more details can be found in Refs. [23]– [25] and [30]– [43].
The probability Pr and the cross section σ of the title reaction are defined as
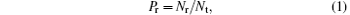

where Nr and Nt are the numbers of reaction trajectories and total trajectories, respectively; while factor bmax is the maximum of the impact parameter.
The rate constant k (T) calculated with the reaction cross section and the Boltzmann integration over the collision energy is given by
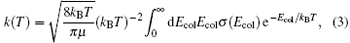
where kB is the Boltzmann constant and Ecol is the collision energy.
A set of PDDCSs represent the full three-dimensional angular distributions, which are associated with three-vector correlations k– k’ – j’ in the CM frame

Function P(θ r) describing the k– j’ correlation is expanded by the Legendre polynomials and P(ϕ r) describing the k– k’ – j’ correlations is expanded in Fourier series

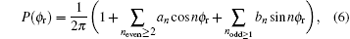
where

The joint probability density function P(θ rϕ r) can be written in the following form:

where

In this calculation, function P(θ r, ϕ r) is expanded up to k = 7, which is sufficient for the convergence. More stereodynamical details of P(θ r), P(ϕ r), and P(θ r, ϕ r) are discussed in the results and discussion.
Figure 2 shows the reaction probability as a function of the collision energy. An equal energy interval is not suitable for the present study, because the values between 0.1 kcal/mol and 1 kcal/mol decrease rapidly which could affect the cross section and the energy-dependent rate constant. Therefore, the energy interval is chosen to be 0.1 kcal/mol between 0.1 kcal/mol and 1 kcal/mol and 0.5 kcal/mol between 1 kcal/mol and 6 kcal/mol. An obvious decline is seen in Fig. 2 with increasing collision energy, which is ascribed to the deep well and barrierless aspect of the PES.
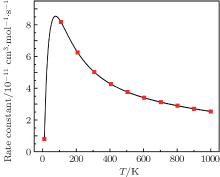
The reaction cross section computed using Eq. (2) is displayed in Fig. 3. As expected for barrierless PESs, the cross section shows no threshold and the maximum appears at 0.1 kcal/mol. As the collision energy increases, the cross section shows a rapid downward trend at 0.1– 1 kcal/mol and a relatively slow circumstance between 1 kcal/mol and 6 kcal/mol, which can be attributed to the decrease of the probability and the maximum of the impact parameter bmax listed in Table 1. Figure 4 illustrates the rate constant with Boltzmann integration over the collision energy at the temperature range of 0– 1000 K. To the best of our knowledge, the rate constants in the previous works are mainly obtained by quantum mechanics (QM) methods, [44– 46] which could take lots of CPU time. In our paper, the QCT method is employed for its less time consumption and better treatment on the relatively low-energy area. As can be seen in the figure, the rate constant displays an increasing trend at 0– 100 K and then decreases with increasing temperature from 100 K to 1000 K, which is similar to other barrierless reactions.[47– 49] Moreover, the distribution of the rate constant also implies that the title reaction favorably occurs at a relatively low-temperature area.
| Table 1. Maxima of the impact parameter (bmax). |
In order to gain an intuitive sight to our results, the stereodynamical information is plotted in three dimensions. The product angular distribution P(θ r) reflecting the k– j’ correlation is presented in Fig. 5. The peaks are centralized at θ r = 90° and symmetrical about 90° , which shows a preference that the rotational angular momentum vector j’ is aligned to the direction perpendicular to the reagent relative velocity k. Additionally, the peaks of P(θ r) become sharper, which implies that the polarization of j’ enhances as the collision energy increases.
 | Fig. 5. Distributions P(θ r) reflecting the k– j’ vector correlations at different collision energies (Ec= 0.1– 6 kcal/mol) for the title reaction. |
Distribution P(ϕ r), which represents the k– k’ – j’ correlation, is plotted in Fig. 6. We have plotted the distributions of Ecol= 0.1 kcal/mol, 3 kcal/mol, and 6 kcal/mol from the inside out to save the space. As can be seen, there are many small peaks and the relatively higher peaks are located at ϕ r = 90° and ϕ r = 270° . The peaks at ϕ r = 90° are higher that those at ϕ r = 270° , which indicates that j’ is favorably aligned with the positive direction of the y axis. This feature may be ascribed to the light-heavy-heavy mass combination. Besides, distributions P(ϕ r) are asymmetric with ϕ r = 180° , which can be explained by the impulsive model constructed by Han and co-workers for the A + BC → AB + C reaction.[1, 4, 23] The j’ is written as j’ = L sin2β + j cos2β + J1mA / mB, where L is the reagent orbital angular momentum and J1mA / mB demonstrates a preferred direction leading to the right-handed DBr molecule rotation. The term cos2β is the mass factor which is defined as cos2β = mA · mC / (mA + mB)(mA + mC). Compared to the H + BrO → HBr + O reaction, [22] the D+ BrO reaction has higher peaks of P(θ r), which implies that the degree alignment of DBr is stronger than that of HBr. Moreover, the P(ϕ r) distribution of D+ BrO is also larger than that of the H+ BrO reaction. The overall enhanced angular distributions of D + BrO → DBr + O can be well explicated by the mass factor and the isotopic effects, which has been meticulously described in the literatures.[50– 53]
 | Fig. 6. Dihedral angle distributions P(ϕ r) with respect to the k– k’ plane depicted from inside out for collision energies Ec = 0.1 kcal/mol, 3 kcal/mol, 6 kcal/mol. |
Figures 7(a)– 7(c) show the joint probability density function P(θ r, ϕ r) to verify the product angular distributions. Obviously, the main peaks are situated at (90° , 90° ) and (90° , 270° ), which are in accordance with distributions P(θ r) and P(ϕ r).
The PDDCSs calculated by the QCT method are depicted in Figs. 8(a) and 8(b). The PDDCS00 (also called the PDDCS (2π /σ )(dσ 00/dω t)) is simply the differential cross section (DCS) that describes the k– k’ correlation only. The PDDCS20 is the so-called expectation value of the second Legendre moments which is associated with the alignment moment 〈 P2(j’ · k)〉 listed in Table 2. Figure 8(a) shows the distribution of PDDCS00 for the collision energy from 0.1 kcal/mol to 6 kcal/mol. We can find that the product forward scattering is enhanced gently while the backward scattering becomes far stronger, which means that as the collision energy increases, the lifetime of the intermediate complex formed in the deep well increases. The PDDCS20 shown in Fig. 8(b) demonstrates a nearly negative scope behavior. Furthermore, it shows an opposite trend compared to PDDCS00, which means that j’ is aligned perpendicular to the reagent relative velocity k. In addition, values of 〈 P2 (j’ · k)〉 indicate that the product rotational alignment of DBr is stronger as the collision energy increases.
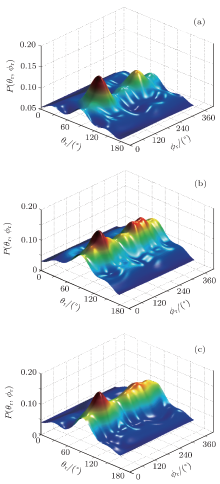 | Fig. 7. Distributions of the joint probability density function P(θ r, ϕ r) at different collision energies: (a) 0.1 kcal/mol, (b) 3 kcal/mol, (c) 6 kcal/mol. |
 | Fig. 8. Distributions of two PDDCSs for the collision energy range of 0.1– 6 kcal/mol: (a) PDDCS00, (b) PDDCS20. |
| Table 2. Rotational alignment parameter 〈 P2 (j’ · k)〉 . |
In this paper, the influence of the collision energy on reaction D + BrO → DBr + O is investigated by using the QCT method. The potential energy surface employed here shows a barrierless behavior with a deep potential well. Scalar properties like the reaction probability, the cross section, and the rate constant are presented. The probability and the cross section show decreasing trends as the collision energy increases, which is ascribed to the barrierless aspect of the PES. The rate constant distribution indicates that the title reaction favorably occurs in a relatively low-temperature region. Meanwhile, vector properties reflecting the k– k’ – j’ correlations are also calculated. Distributions P(θ r), P(ϕ r), and P(θ r, ϕ r) reveal that with increasing collision energy, the product rotation prefers an out-of-plane rather than an in-plane reaction mechanism. The PDDCSs demonstrate a stronger product forward and backward scattering, which means that the polarization of the rotational angular momentum j’ enhances and the lifetime of the intermediate complex increases. In summary, there are obvious collision energy effects on the vector and scalar properties of the D + BrO → DBr + O reaction.
We thank Prof. Han Ke-Li for providing the stereodynamics program. We acknowledge the High Performance Computing Center (HPCC) of Jilin University for the supercomputer time.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|