Cite this Article
Liu Yu, Zhai Liang-Jun, Wang Huai-Yu†. Theoretical study of mutual control mechanism between magnetization and polarization in multiferroic materials* . Chinese Physics B, 2015, 24(3): 037510  
Permissions
Theoretical study of mutual control mechanism between magnetization and polarization in multiferroic materials*
Liu Yu, Zhai Liang-Jun, Wang Huai-Yu†
Department of Physics, Tsinghua University, Beijing 100084, China

†Corresponding author. E-mail: wanghuaiyu@mail.tsinghua.edu.cn

*Project supported by the National Basic Research Program of China (Grant No. 2012CB927402) and the National Natural Science Foundation of China (Grant Nos. 61275028 and 11074145).

Abstract

The mutual control mechanism between magnetization and polarization in multiferroic materials is studied. The system contains a ferromagnetic sublattice and a ferroelectric sublattice. To describe the magneto–electric coupling, we propose a linear coupling Hamiltonian between ferromagnetism and ferroelectricity without microscopic derivation. This coupling enables one to retrieve the hysteresis loops measured experimentally. The thermodynamic properties of the system are calculated, such as the temperature dependences of the magnetization, polarization, internal energy and free energy. The ferromagnetic and ferroelectric hysteresis loops driven by either a magnetic or an electric field are calculated, and the magnetic spin and pseudo-spin are always flipped synchronously under the external magnetic and electric field. Our theoretical results are in agreement with the experiments.

Keyword: 75.85.+ t; 75.40.cx; 75.80.+ q; 77.80.- e; multiferroic materials; mutual control mechanism; ferromagnetic and ferroelectric hysteresis loops; Green's function
1. Introduction

Multiferroic materials are a kind of compound, and in each of them the magnetic and electric orders coexist below a certain temperature. The interaction between the two types of orders, called magnetoelectric (ME) coupling, yields some additional features to the ferroelectric and magnetic transitions and introduces possible multifunctional responses to an external electric or magnetic field.[1– 5] The mutual effect between the magnetic and electric orders makes these compounds ideal for applications in information storage, in the emerging field of spintronics, and sensors.[6] Moreover, because of the complex physical mechanism and the interesting phenomena of the multiferroic materials, theoretical researches of the ME effect are also attractive for fundamental physics.[7– 14]

Theoretical studies can be carried out by either macroscopic or microscopic approaches. The first theoretical attempt of studying the ME coupling proposed a term of α ijEiHj in the free energy based on group theory, [15] where E and H represented the electric and magnetic fields, respectively, and i and j label the Cartesian coordinates. Based on this phenomenological theory, ME coupling was explained under the macroscopic approximations.[9, 16, 17] On the other hand, the possible microscopic origins of the ME coupling were proposed and the relevant thermodynamic properties were studied in the microscopic studies.[7, 18– 21] The dielectric and magnetic properties of multiferroic materials were simulated by use of t he Monte Carlo method.[22] The Heisenberg model for magnetic interaction and single-well potential model for electrical interaction were applied to analyze the ME effects in the ferroelectric (FE)-antiferromagnetic (AFM) system.[23] The magnetic and electric static and dynamic properties of hexagonal multiferroic RMnO3 were studied based on the transverse Ising and Heisenberg models.[24] In a recent work, [25] Landau's theory for the phase transitions of the second kind was utilized to study the electric orders in a FE-ferromagnetic (FM) system. However, this theory was applicable to the case that the temperature is very close to the transition point. In that work, the calculated free energy of a multiferroic system increased as temperature rose, which contradicted the second law of thermodynamics. In spite of these theoretical works, the study of the microscopic mechanism of the mutual control between magnetization and polarization has been seldom seen. For example, there has been little work that could draw the magnetic hysteresis loops driven by an external electric field. Revealing the mechanism behind the hysteresis loops is still desirable.

In the present work, we investigate the microscopic mutual control mechanism between magnetization and polarization, and relevant thermodynamics in multiferroic materials. The thermodynamic properties and the affection of external fields are studied in detail by making use of the double-time Green's function method. This paper is organized as follows. In Section  2 the Hamiltonian of multiferroic materials is presented, and the system of FM– FE is considered. In Section  3, the numerical results of the temperature dependences of intrinsic energies, free energies, magnetization, and polarization are presented. The ferromagnetic and ferroelectric hysteresis loops driven by the external magnetic and electric fields are studied, respectively. Finally, Section  4 gives our conclusion.

2 Model and method

In this work, a simplest construction is assumed: the FM and FE sublattices are both simple cubic and are nested with each other; that is, the nearest neighbors of a FM (FE) site are the FE (FM) ones, while the next-nearest sites are those in the same sublattice. The Hamiltonian of the multiferroic system can be presented as[7, 19– 21]

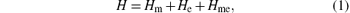
where Hm and He denote the Hamiltonians for the FM and FE subsystems, respectively, and Hme describes the ME coupling between the two subsystems.

The FM subsystem is described by the Heisenberg model and the spontaneous magnetization is along the z direction. The Hamiltonian reads[26, 27]

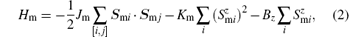
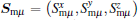
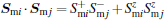
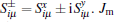
where is the spin at site i. One can write where represents the exchange integral between the magnetic lattice sites, [i, j] denotes the nearest-neighbor sites in the FM sublattice, Km2 is an anisotropy parameter, and Bz is the external magnetic field along z direction. In this paper, we set kB = 1.

The FE subsystem is modeled by the transverse Ising model, which can be written as[28]

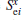
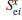
where and are the spin-1/2 operators of the pseudo-spins, which obey the commutation relation of convenient spin operators. Je denotes the interaction between adjacent electric lattice sites, and Ω is the tunneling frequency.

The coupling term is the most important part in constructing the Hamiltonian since it should be invariant with respect to time reversal and spacial inversion. Different forms of the coupling term between the magnetic and electric subsystems have been proposed in the previous studies. In the phenomenological treatment, the coupling term usually take the form of P2M2, [29] or P· M(∇ · M), [30] where P and M are polarization and magnetization, respectively. 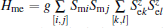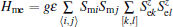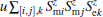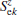In the microscopic study, the general form of ME coupling is written as , [7, 23] where g is the coupling constant, by which the FM and FE subsystems have independent phase transition temperatures. When the magnetic subsystem is an AFM structure, the coupling term was written as .[8, 18, 19] Here, the AFM subsystem was separated into two magnetic sublattices, and 〈 i, j〉 denotes the nearest-neighbor of the magnetic sublattice. The ɛ = 1 if both i and j belong to the first sublattice; and ɛ = -1 if both belong to the second sublattice, ɛ = 0 otherwise. In recent studies, [21, 31] a different form of ME coupling was proposed as , in which the coupling constant u was a pseudoscalar, i.e., for the total coupling term is invariant, the coupling constant u should change sign when the sign of is changed.

The proposed forms of coupling demonstrate that the construction of the coupling term is still controversial. However, the above microscopic coupling forms cannot well describe the found phenomena of the magnetic hysteresis loops driven by the electric field (E– M loops) and the electric hysteresis loops driven by the magnetic field (B– P loops).[32– 37] From the expressions of the proposed coupling term, it is found that the exchange integral between the magnetic (electric) lattice sites is modulated by the variation of polarization (magnetization) when an external electric (magnetic) field is applied, but the sign of magnetization (polarization) will not change. Recent experimental studies have shown that the magnetization and polarization can be flipped synchronously by the external magnetic and electric field.[36, 37] Based on these experimental results, we propose a form of the ME coupling as

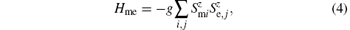
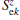
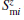
where the coupling parameter g is an invariant because we do not have any reason why it should change its sign when the sign of or changes. Our proposed coupling term Eq.  (4) is not derived from a microscopic mechanism of a multiferroic. We use this form because it can reveal two features, as follows. On the one hand, when one of the polarization and magnetization changes its sign, the other should change its sign as well to keep the total coupling invariant. On the other hand, the magnetization (polarization) could serve as an external electric (magnetic) field via the ME coupling. Accordingly, the phase transition temperatures of magnetic and electric subsystems could be very close to each other, which is consistent to the case of spin order induced multiferroics.[2]

For the FM subsystem, the Hm and Hme can merge to be an effective magnetic Hamiltonian

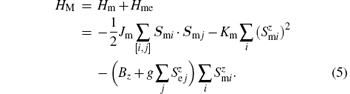
It is seen that the polarization serve as an external field on the magnetization, therefore, an effective magnetic field is defined as

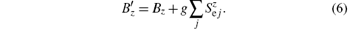
On the other hand, an effective FE Hamiltonian can also be defined as

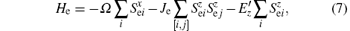
where 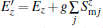is the effective electric field.

We use the method of double-time Green's function to solve the system. For the FM subsystem, the Greens' function is

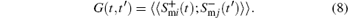
The Green's function can be treated following the standard routine, [38– 40] and we do not intend to present the tedious formalism. For the FE subsystem, we use the creation and annihilation operators of Fermion type ai+ and aj+ + to construct the Green's functions of the electric subsystem[28] G'i, j (t, t')= 〈 〈 ai+ (t); aj+ + (t)〉 〉 . The thermo-average of z component of the pseudo-spins can be expressed following the standard routine proposed in Ref.  [28].

3 Results and discussion
3.1 Thermodynamics

We set the parameters as Jm = 50, Km = 0.5, Sm = 2, and Je= 100, Ω e = 1. In the absence of ME coupling, the phase transition temperature of the FM subsystem is higher than that of the FE subsystem. Once the ME coupling is nonzero, the FM and FE subsystems should have close phase transition temperatures, since the magnetization serves more or less as the external field via the ME coupling.

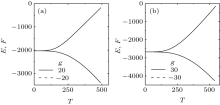
In a recent study, the free energy of the multiferroic material was calculated in order to investigate the thermal hysteresis phenomenon.[25] It was concluded that free energy grew with temperature for two solutions S+ + (both magnetization and polarization were positive) and S+ - (magnetization was positive and polarization was negative). The free energy for S+ + vanished at a certain temperature, which leads to the thermal hysteresis phenomenon.

Based on our present Hamiltonian Eq.  (1), we also calculate the free energies of the two possible configurations S+ + and S+ -. The coupling constant g should be positive for S+ + and negative for S+ -. As long as one configuration is fixed, the corresponding coupling constant g remains unchanged, whether or not magnetization or polarization reverses under an external field. The formula for evaluating the free energy F(T) is

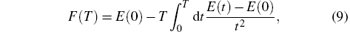
where E(T) is the internal energy of the multiferroic material, which is calculated as the statistical average of the Hamiltonian. The internal energy should increase with temperature, or the specific heat would be negative. Consequently, as implied by Eq.  (9), the free energy should decrease with temperature.

Figure  1 plots the internal energy and free energy of the configuration S+ + with g= 20 and 30 and those of S+ - with g= -20 and -30. As long as the coupling strength is fixed, the energies are unchanged, no matter which configuration is used. Therefore, the solid and dashed lines in each panel of Fig.  1 are the same. The configuration with higher coupling strength has lower energy values. It is shown that E always increases while F decreases with temperature, as anticipated. We can also find that the solutions of the configuration S+ + are always identical to that of S+ -, and an obvious fact is that the free energies do not vanish at any temperature, a conclusion different from that of Ref.  [25]. Since there is no difference in physical quantities between the two configurations, in the following, we only consider the configuration S+ + .

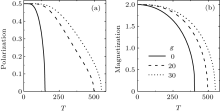
Fig.  1. The internal energy (ascending curves) and free energy (descending curves) of configurations S+ + and S+ - for (a) g= ± 20 and (b) g= ± 30. In each panel, the solid and dashed lines are identical.

In Fig.  2, the temperature dependences of polarization and magnetization for g= 0, 20, 30 are plotted. In the absence of ME coupling, the phase transition temperature of the magnetic subsystem is higher than that of the electric subsystem. The magnetization serves as the external field via the ME coupling when g is nonzero, which leads to the phase transition of electric subsystem shifts upward. With the growth of coupling strength, the phase transition temperatures of both the magnetic and electric subsystems are enhanced. The numerical results demonstrate that when the linear coupling term is adopted, both the magnetic and electric subsystems do not have independent phase transition temperatures. Such behavior is basically consistent with the experimental results of the multiferroic material induced by spin order.[41, 42]

Fig.  2. The temperature dependence of (a) polarization and (b) magnetization for g= 0, 20, 30.

3.2 The mutual effect between the magnetization and polarization

One important feature of multiferroic materials is the mutual control between the magnetization and polarization; that is, the magnetization (polarization) could be controlled by an external electric (magnetic) field. Although the E– M loops and B– P loops were measured, microscopic theoretical studies have hardly been seen. Our present model enables us to study the properties of mutual control between magnetization and polarization.

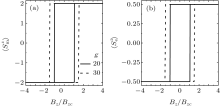
In Fig.  3, the magnetic hysteresis loops driven by the magnetic field (B– M loops) and B– P loops at T= 30 and g= 20 and 30 are plotted. Note that the external magnetic field is rescaled by Bzc, which is the coercivity of B– M loop of g= 20 and T= 30. By comparison with Figs.  3(a) and 3(b), it is clear that the coercivity of B– P loop is always the same as that of B– M loop at a given coupling. In other words, the pseudo-spin and magnetic spin are flipped synchronously by the magnetic field, which is in agreement with the experimental result of CoCr2O4.[36] The synchronous flipping originates from the linear coupling between magnetization and polarization, as reflected in Eq.  (4).

Fig.  3. (a) The H– M loops and (b) H– P loops at T= 20 for two g values.

It is found that the coercivities of both the B– M and B– P loops increase with the increase of g, which may be contrary to our intuition of the mutual control between magnetization and polarization, but such behavior can be easily understood by evaluating the variation of the effective magnetic field B'z, see Eq.  (6). In the case of the decreasing process of the external magnetic field, we assume that the magnetic spin flips at Bz= – Bz0 (Bz0 is positive) in the absence of ME coupling. When the ME coupling g is nonzero, the magnetic spin flips at B'z = – Bz0. From Eq.  (6), the applied magnetic field is written as

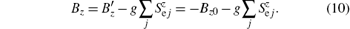
Thus, the applied magnetic field increases with the increase of g, and the coercivity grows with g. Moreover, since the pseudo-spin always flips synchronously with magnetic spin, the coercivity of B– P loop also grows with g .

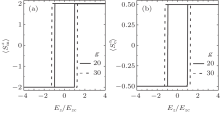
The E– M loops and the electric hysteresis loops driven by the electric field (E– P loops) at T= 30 and g= 20 and 30 are plotted in Fig.  4, where the external electric field is rescaled by the coercivity of E– P loop of g= 20 and T= 30 Ezc. We find that the pseudo-spin and magnetic spin can be flipped synchronously by the electric field, which is consistent with the experimental study.[37] The coercivities of the E– M and E– P loops also grow with g, which can also be properly understood by evaluating the relations between effective electric field E'z in Eq.  (7) and the ME coupling.

Fig.  4. (a) The E– M loops and (b) E– P loops at T= 20 for two g values.

4 Conclusion

In this paper, the mutual control mechanism between magnetization and polarization, and the relevant thermodynamic of the multiferroic materials, in which FM and FE orders coexist, have been studied by use of the double-time Green's function method. The calculated free energy always decreases with temperature and does not vanish for either configuration S+ + or S+ -. A ME coupling Hamiltonian is proposed, which enables one to retrieve the E– M and B– P loops measured experimentally. Through the study of the mutual effect of the magnetic and electric subsystems, we have found that the electric or magnetic field can always overturn the magnetization and polarization simultaneously as long as the ME coupling does not vanish, and such theoretical results agree very well with the experiments. We also find that the increase of coupling coefficient could increase the coercivities of the hysteresis loops. Finally, the authors confess that the proposed ME coupling Hamiltonian Eq.  (4) is not derived from a definite microscopic physical mechanics. We shall try this derivation to explore the solid foundation of this coupling.

Reference
1 Spaldin N A 2005 Science 309 391 DOI:10.1126/science.1113357 [Cited within:1]
2 Wang K F, Liu J M and Ren Z F 2009 Adv. Phys. 58 321 DOI:10.1080/00018730902920554 [Cited within:1] [JCR: 34.294]
3 Spaldin N A, Cheong S W and Ramesh R 2010 Phys. Today 63 38 DOI:10.1038/nmat1804 [Cited within:1] [JCR: 6.762]
4 Cheong S W and Mostovoy M 2007 Nat. Mater. 6 13 DOI:10.1038/nmat1804 [Cited within:1] [JCR: 35.749]
5 Song G L, Luo Y P, Su J, Zhou X H and Chang F G 2013 Acta Phys. Sin. 62 97502(in Chinese) DOI:10.7498/aps.62.097502 [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
6 Scott J F 2012 J. Mater. Chem. 22 4567 DOI:10.1039/c2jm16137k [Cited within:1] [JCR: 5.968]
7 Wesselinowa J M and Kovachev S 2007 J. Appl. Phys. 102 043911 DOI:10.1063/1.2767377 [Cited within:4] [JCR: 0.71]
8 Gao X S, Liu J M, Li Q C and Liu Z G 2001 Ferroelectrics 252 69 DOI:10.1080/00150190108016242 [Cited within:1] [JCR: 0.415]
9 Nan C W, Liu G, Lin Y and Chen H 2005 Phys. Rev. Lett. 94 197203 DOI:10.1103/PhysRevLett.94.197203 [Cited within:1] [JCR: 7.943]
10 Cao K and He L X 2014 Physics 43 157(in Chinese) DOI:10.7693/wl20140302 [Cited within:1] [CJCR: 0.2383]
11 Mochizuki M and Furukawa N 2009 Phys. Rev. B 80 134416 DOI:10.1103/PhysRevB.80.134416 [Cited within:1]
12 Katsura H, Nagaosa N and Balatsky A V 2005 Phys. Rev. Lett. 95 057205 DOI:10.1103/PhysRevLett.95.057205 [Cited within:1] [JCR: 7.943]
13 Sergienko I A and Dagotto E 2006 Phys. Rev. B 73 094434 DOI:10.1103/PhysRevB.73.094434 [Cited within:1]
14 Xiang H J, Kan E J, Zhang Y, Whangbo M H and Gong X G 2011 Phys. Rev. Lett. 107 157202 DOI:10.1103/PhysRevLett.107.157202 [Cited within:1] [JCR: 7.943]
15 Land au L D and Lifshitz E M 1984 Electrodynamics of Continuous MediaMoscow Ed. MIR [Cited within:1]
16 Nan C W 1994 Phys. Rev. B 50 6082 DOI:10.1103/PhysRevB.50.6082 [Cited within:1]
17 Wang X, Pan E and Albrecht J D 2008 J. Appl. Phys. 103 113511 DOI:10.1063/1.2939263 [Cited within:1] [JCR: 0.71]
18 Gehring G A 1994 Ferroelectrics 161 275 DOI:10.1080/00150199408213376 [Cited within:2] [JCR: 0.415]
19 Gao X S, Liu J M, Chen X Y and Liu Z G 2000 J. Appl. Phys. 88 4250 DOI:10.1063/1.1309053 [Cited within:2] [JCR: 0.71]
20 Bahoosh S G, Wesselinowa J M and Trimper S 2013 Phys. Status Solidi B 249 1602 DOI:10.1002/pssb.201248059 [Cited within:1] [JCR: 1.489]
21 Bahoosh S G and Wesselinowa J M 2013 J. Appl. Phys. 113 063905 DOI:10.1063/1.4791586 [Cited within:3] [JCR: 0.71]
22 Li Q C and Liu J M 2007 Phys. Rev. B 75 064415 DOI:10.1103/PhysRevB.75.064415 [Cited within:1]
23 Zhong C G, Mu R W and Fang J H 2005 Solid State Commun. 135 759 DOI:10.1016/j.ssc.2005.05.004 [Cited within:2] [JCR: 1.534]
24 Bahoosh S G and Wesselinowa J M 2012 Phys. Status Solidi B 249 2227 DOI:10.1002/pssb.201248297 [Cited within:1] [JCR: 1.489]
25 Livesey K L and Stamps R L 2010 Phys. Rev. B 81 064403 DOI:10.1103/PhysRevB.81.064403 [Cited within:3]
26 Wang H Y, Jen S U and Yu J Z 2006 Phys. Rev. B 73 094414 DOI:10.1103/PhysRevB.73.094414 [Cited within:1]
27 Wang H Y and Xun K 2006 Phys. Rev. B 74 214425 DOI:10.1103/PhysRevB.74.214425 [Cited within:1]
28 Teng B and Sy H K 2004 Phys. Rev. B 70 104115 DOI:10.1103/PhysRevB.70.104115 [Cited within:3]
29 Kimura T, Kawamoto S, Yamada I, Azuma M, Takano M and Tokura Y 2003 Phys. Rev. B 67 180401 DOI:10.1103/PhysRevB.67.180401 [Cited within:1]
30 Mostovoy M 2006 Phys. Rev. Lett. 96 067601 DOI:10.1103/PhysRevLett.96.067601 [Cited within:1] [JCR: 7.943]
31 Apostolova I N 2014 J. Appl. Phys. 115 064103 DOI:10.1063/1.4865270 [Cited within:1] [JCR: 0.71]
32 Hur N, Park S, Sharma P A, Guha S and Cheong S W 2004 Phys. Rev. Lett. 93 107207 DOI:10.1103/PhysRevLett.93.107207 [Cited within:1] [JCR: 7.943]
33 Weber S, Lunkenheimer P, Fichtl R, Hemberger J, Tsurkan V and Loidl A 2006 Phys. Rev. Lett. 96 157202 DOI:10.1103/PhysRevLett.96.157202 [Cited within:1] [JCR: 7.943]
34 Yamasaki Y, Miyasaka S, Kaneko Y, He J P, Arima T and Tokura Y 2006 Phys. Rev. Lett. 96 207204 DOI:10.1103/PhysRevLett.96.207204 [Cited within:1] [JCR: 7.943]
35 Hur N, Park S, Sharma P A, Ahn J S, Guha S and Cheong S W 2004 Nature 429 392 DOI:10.1038/nature02572 [Cited within:1] [JCR: 38.597]
36 Yamasaki Y, Miyasaka S, Kaneko Y, He J P, Arima T and Tokura Y 2006 Phys. Rev. Lett. 96 207204 DOI:10.1103/PhysRevLett.96.207204 [Cited within:2] [JCR: 7.943]
37 Zhao T, Scholl A, Zavaliche F, Lee K, Barry M, Doran A, Cruz M P, Chu Y H, Ederer C, Spaldin N A, Das R R, Kim D M, Baek S H, Eom C B and Ramesh R 2006 Nat. Mater. 5 823 DOI:10.1038/nmat1731 [Cited within:3] [JCR: 35.749]
38 Tyabikov S V 1967 Methods in the Quantum Theory of Magnetism New York Plenum Press [Cited within:1]
39 Wang H Y 2012 Green's Function in Condensed Matter Physics Oxford Alpha Science Intl Ltd [Cited within:1]
40 Wang H Y, Zhai L J and Qian M 2014 J. Magn. Magn. Mater. 354 309 DOI:10.1016/j.jmmm.2013.11.024 [Cited within:1] [JCR: 1.826]
41 Subramanian M A, He T and Chen J Z 2006 Adv. Mater. 18 1737 DOI:10.1002/(ISSN)1521-4095 [Cited within:1] [JCR: 14.829]
42 Mo H, Nelson C H, Bezmaternykh L N and Temerov V T 2008 Phys. Rev. B 78 214407 DOI:10.1103/PhysRevB.78.214407 [Cited within:1]