ZnO-based diluted magnetic semiconductors (DMSs), ^{[1, 2]} which exhibit both semiconductor properties and ferromagnetism above room temperature (RTFM), ^{[3, 4]} have attracted long-lasting interest in the past decades due to their superior physical properties and application potentials in spintronic devices.^[5] Normally, the ferromagnetism in ZnO can be obtained by substituting Zn²⁺ with transition metal ions or induced by defects.^{[6– 14]} However, for the transition metal-doped ZnOs, they suffer from extrinsic impurity magnetic clusters. This motivates the study of nonmagnetic ion-doped ZnO, e.g., Cu-doped ZnO (ZnO:Cu), as neither metallic copper nor its oxide segregation is ferromagnetic nature above room temperature. It has been found by theoretical calculations and experimental observations, ^{[15– 25]} that ZnO:Cu is ferromagnetic in nature, which can also been greatly tailored by the concentration of charge carriers or defects.^{[10, 26– 30]} More interestingly, by properly adjusting the doping level and processing parameters, Cu-doped ZnO can show an electrical polarization in addition to its ferromagnetism, making it a possible new candidate for multiferroics.^[31]

In spite of the numerous investigations on the magnetic properties of ZnO:Cu, there are still few investigations addressing tailoring of its magnetic properties by an external field, e.g., electric field, pressure, strain or stress, although it is rather essential for spintronics or magnetoelectric applications. For instance, in certain ferroelectric/magnetic heterostructure, the magnetic properties can be altered by the interface strain originating from an electric field, enabling the electric control of magnetic states.^{[32, 33]} In this work, we explored the effect of uni-axis pressure on the magnetic properties on ZnO:Cu. It is found that c-axis pressure at around 8  GPa can lead to a dramatical change in ferromagnetic stability, accompanied with a structural transformation from wurtzite to graphite-like structure. This provides an effective way to tailor its magnetic properties through external pressure or interface strains.

The theoretical calculations were performed using the Cambridge Serial Total Energy Package (CASTEP), ^[34] which   employs the density functional theory plane-wave pseudopotential method. Here, the exchange correlation functional was described by the generalized gradient approximation (GGA)^[35] in the form of Perdew– Bruke– Eruzerhof (PBE). To describe the ionic cores, the ultrasoft pseudopotentials^[36] with 3d¹⁰4s¹, 2s²2p⁴, and 3d¹⁰4s² valence electron configurations were used for Cu, O, and Zn atoms, respectively, and the cutoff energy for the plane wave basis was set to be 550  eV in all computations. Initially, the ZnO crystal was a 2× 2× 2 supercell with a total number of 32 atoms. The Brillouin zone was sampled by 5× 5× 4 special k-points for the supercell. The convergence threshold was set to be 1× 10^-6  eV in energy and 0.01  eV/Å in force. All these parameters have been tested carefully to ensure the convergence of the energies and force wells. Before calculating the static properties, the cell structure has been optimized under the applied pressure and its atomic locations have been fully relaxed by the Broyden– Fletcher– Goldfarb– Shanno (BFGS) algorithm.

We first optimized the structure for pure ZnO, which produces a wurtzite structure with a= 3.281  Å and c= 5.295  Å . These results are in good agreement with the previous experimental reports^{[37, 38]} and first-principles results.^{[15, 16, 19, 39]} Then we calculated the ZnO:Cu, in which two copper atoms were placed in the two zinc sites within a 2× 2× 2 supercell, producing a doping level of 12.5%. As shown in Fig.  1(a), there are five different possible substitution configurations. For instance, if we place one copper atom in location “ 0” , and there are five different possible locations for the other copper atoms to go in the supercell, forming five different substitution configurations. For simplicity, we use conf-n to denote the different configurations with the Cu pair at (0, n) sites. Here, we systematically calculated the relative total energies for both ferromagnetic (FM) and antiferromagnetic (AFM) states of the five different configurations, as listed in Table  1.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. The structure for the 32-atom supercell with two Cu atoms used in this calculation: (a) Wurtzite structure at zero pressure; (b) graphite-like structure ouccrs at 8  GPa. The numbers 0 to 5 represent the six possible sites for a Cu atom to substitute a Zn atom, in which we fix the first Cu atom on site 0, and place the other Cu atoms on the five possible Zn sites, producing five different configurations.

Table 1.

Table 1.

Table 1. The relative total energies for the five different configurations, EFM presents the energy for ferromagnetic order, and EAFM is the energy for antiferromagnetic order. The energy for each configuration was normalized by subtracting the EFM of Conf-2, respectively. Conf. 1 2 3 4 5 EFM/eV 0.07967 0 0.26221 0.26548 0.24956 EAFM/eV 0.24766 0.14652 0.26903 0.27069 0.26731

Table 1. The relative total energies for the five different configurations, EFM presents the energy for ferromagnetic order, and EAFM is the energy for antiferromagnetic order. The energy for each configuration was normalized by subtracting the EFM of Conf-2, respectively.

From Table  1, one can see that the FM state of conf-2 (the two copper atoms occupy the two nearest zinc sites in the ab-plane) has the lowest energy among of all the five configurations. This indicates that the Cu²⁺ ions have a tendency to aggregation, which coincides with the previous calculations.^{[15, 16, 18, 21]} The FM state for each of the configurations shows lower energy than that of the corresponding AFM state, indicating the FM state is the more favorite state. To verify the Coulomb U effect on the ferromagnetic properties, we also applied the GGA+ U^{[40, 41]} correction (U= 4  eV on Cu 3d electrons)^[15] to calculate the total energies for all the five configurations, which produce a similar evolution trend. Based on the above results, we can conclude that conf-2 is the most stable configuration, which has the highest probability to appear in Cu-doped ZnO. Therefore, in the following sections, we will mainly focus on conf-2.

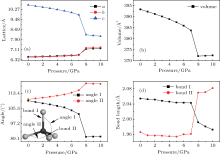
At first, we calculated the evolution of ZnO:Cu lattice structure under c-axis pressure. Figures  2(a) and 2(b) demonstrate the evolution of lattice parameters and unit cell volume with respect to various pressures. As pressure increases from 0 to 7  GPa, the lattice parameters along a and b increase, parameter c and cell volume decrease slightly. A sudden structural change occurs when the pressure reaches 8  GPa, in which one can see that the lattice parameter c drops down about 12%, while a and b increase for about 5%, resulting in a total volume shrinkage of 3%. At the same time, an apparent change in bond angle and bond length can also be identified from Figs.  2(c) and 2(d), wherein the bond angle-num1 drops down to 90° , angle-num2 enlarges to 120° , accompanied with an increase in bond length num1 and a decrease in bond length num2, simultaneously. The dramatic structural change clearly indicates the formation of a new structure, which is so called graphite-like structure (see Fig.  1(b)), as has been reported theoretically by Kulkarni et al.^[42] and Yadaw et al.^[43] in ZnO nanostructures as well as Xu et al. in ZnO single crystal.^[44]

In order to get a clear picture of the effects of c-axis pressure on the magnetic properties of ZnO:Cu, we have performed a systematic calculation on ferromagnetic energy and stability as a function of c-axis pressure. As shown in Fig.  3(a), the total energy in the supercell for both FM and AFM states increases slightly first at a pressure range of 0– 7  Gpa, and it rises up sharply when the pressure further increases to 8  GPa. It is noted that the FM states exhibit a lower energy than those of AFM states over the whole pressure range, indicating that FM states are the more energetic favorable states. However, at pressures of above 8  GPa, the two total energies (both FM and AFM) almost overlap with each other, indicating a loss of stability of the FM state. This is also confirmed by the pressure dependent energy difference (Δ E), as shown in Fig.  3(b). The Δ E first increases gradually from 141  meV to 171  meV when pressure rises from 0 to 5  GPa, then becomes more or less stable up to 7  GPa, and finally drops down sharply to nearly zero when pressure goes beyond 8  GPa. In general, the stability of the FM state can be quantified by Δ E, which is also strongly related to magnetic Curie temperature T_c.^[45] The reduction in Δ E indicates a loss of ferromagnetic stability in ZnO:Cu induced by c-axis pressure, which leads to a magnetic state transformation from the FM state to a paramagnetic (PM) like state. Noted that the above transition pressure is coincident with that of structural transition, the magnetic transformation most probably resulted from structural change (shown in Fig.  2).

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Evolution of cell structure as a function of c-axis pressure: (a) lattice parameters; (b) volume; (c) bond angle; (d) bond length. The insert shows the schematic diagram of the bond angles marked Angle-numI, Angle-numII, Bond num1, and Bond numII.

Fig.  3.

	Figure Option ViewDownloadNew Window
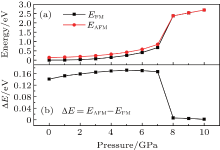	Fig.  3. The crystal energies at the FM and AFM states and the energy difference (Δ E) between FM and AFM states as a function of c-axis pressures: (a) energy and (b) Δ E.

The local spin moment for each atom has also been calculated by atomic population analysis. It was found that the local spin moment for each Cu atom is of 0.58μ _B (μ _B is the Bohr magneton), together with the neighboring spin polarized Os of 0.42μ _B, producing a total spin moment for the unit cell of 2μ _B. This agrees with the theoretical calculation results by Ye et al.^[16] As pressure increases to 8  GPa, both the supercell total spin moment and the local spin moment for each Cu remain unchanged, while the spin distribution in the neighboring oxygen varies. The spin moment for the oxygen located between two Cu atoms declines from 0.26μ _B to 0.14μ _B, while at the top and bottom sites of the copper atoms, the local moment increases from 0.06μ _B to 0.10μ _B.

Figure  4 shows the total and partial densities of states (DOS) of ZnO:Cu for Conf-2 at pressures of 7  GPa and 8  GPa. From the total DOS, one can see that for both 7  GPa and 8  Gpa, they show half metallic characteristic, with high spin polarization up to 100%. In addition, the Cu-3d states have a strong hybridization with O 2p states at the Fermi level. This favors the p– d exchange interaction which mediates the coupling between the Cu²⁺ ions, leading to the stable FM ordering. In contrast, at 8  GPa the state densities for Cu-3d and O-2p near the Fermi level have greatly changed, and the p– d hybridization becomes less apparent, corresponding to a lower magnetic stability. This is also confirmed by the different levels of spin electron density overlap between Cu²⁺ and O^2-, which is very essential in determining the strength of the magnetic exchange, as will be further discussed below.

Fig.  4.

	Figure Option ViewDownloadNew Window
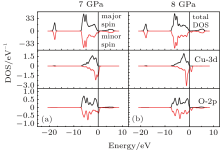	Fig.  4. Total DOS and partial DOS for the Cu-doped ZnO with Cu-3d and O-2p under c-axis pressure of 7  GPa (a) and 8  GPa (b). The energy is represented with respect to the Fermi level.

In order to further understand the origin of magnetic transition, the spin– charge density has been calculated and shown in Figs.  5(a) and 5(b). One can see that there are two different shapes of spin– charge density distribution for both copper atoms with and without pressure. This is due to the change of spin electron orbitals affected by different crystalline field environments due to structural transition. At 0  GPa, the Cu²⁺ located in the center of the tetrahedral field formed by four neighboring O^2-. While at the 8  GPa, the Cu²⁺ is located in the trigonal bipyramidal field formed by the five neighboring O^2-. As the electron state for Cu²⁺ is 3d⁹, there is only one single electron carrying spin moment. The change of the crystalline field from tetrahedral to trigonal bipyramidal structures altered the spin electron orbitals, hence greatly affected the distribution of spin– charge densities around Cu and O.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Spin– charge density distribution for the Cu-doped ZnO at two different pressures: (a) 0 GPa; (b) 8 GPa; enlarged spin– charge density distribution near the Cu– O bonds (the O atom connected with two Cu atoms in ab-plane) at different pressures: (c) 0  GPa and (d) 8  GPa.

The spin– charge density at the Cu– O bond (where an O atom bridging the two Cu atoms) was also illustrated in Figs.  5(c) and 5(d). When a large pressure is applied to induce the structural transition (e.g., 8  GPa), the spin– charge density distribution is significantly varied, owing to the crystalline field change, in particular the elongating of bond length between Cu and O. This is also accompanied with an apparent diminishing of the overlapping between the p– d orbitals. This can also interpret the observed loss of magnetic stability Δ E, which is greatly depended on the exchange coupling between two adjacent Cu atoms mediated by the spin electron exchange between O 2p and Cu 3d orbits. As a result, the sharp drop in spin– charge density overlapping can thus lead to the sudden change in ferromagnetic stability from a FM state to a nearly zero Δ E state, corresponding to the observed PM-like ground state.

It is worth of mentioning that the above calculation is based only on a single configuration of Cu-doping and largely ignores other possible configurations, although their probability is not as high as Conf-2. For this, we also calculated the difference in total energies between FM and AFM states (Δ E) for all the configurations subjected to high pressure (10  GPa) along the c-axis. As shown in Table  2, the Δ E in Confs: 1, 2, 3, 5 declines nearly to zero at 10  GPa, while for Conf-4, the Δ E drops down to -100  meV corresponding to an AFM order. This indicates that under a high pressure, the configuration evolves either from FM to PM state, or from FM to AFM state, resulting in an overall reduction in ferromagnetism. This provides us with an effective way to tailor the magnetic properties of DMS by an external pressure, interfacial strain, or other external fields.

Table 2.

Table 2.

Table 2. Energy difference (Δ E) between FM and AFM orders for the five configurations at c-axis pressure of 0  GPa and 10  GPa. Conf. 1 2 3 4 5 Δ E/meV 0  GPa 168 147 6.8 5.2 17.8 10  GPa 9.5 1.9 -4.3 -109 -16.7

Table 2. Energy difference (Δ E) between FM and AFM orders for the five configurations at c-axis pressure of 0  GPa and 10  GPa.

In summary, we have investigated the influence of c-axis pressure on the structure and magnetism for ZnO:Cu DMS using the first principles calculations. It is shown that when pressure increases from 0 to 10  GPa along the c-axis, there occurs a structural phase transition accompanied with a significant drop in magnetic stability, indicating the occurrence of FM to PM transformation. We also found that the stability of FM is also greatly correlated with the degree of overlapping of the spin– charge of Cu²⁺ and O^2- in the ab-plane, in association with the p– d exchange interaction that mediates the coupling between the spin ions.