Recently, the magnetic refrigeration based on magnetocaloric effect (MCE) that uses an external magnetic field to change the magnetic entropy of magnetic materials, has attracted much attention due to its higher energy efficiency and lower environmental influence than the conventional gas compression refrigeration.^{[1– 3]} Although new materials with giant MCE near room temperature have been studied for applications, materials with giant MCE in the low-temperature region from about 30  K down to sub-Kelvin temperatures are also essential for utilization in certain fields, such as gas liquefaction.^[1] Helium plays a significant role in low-temperature scientific research and cryogenic engineering.^[4] Generally, helium gas needs to be cooled down to liquid form for its storage and transportation. Therefore, it is significant to develop advanced magnetic refrigerants with large MCE around the liquid helium temperature (4.2  K). In addition, most of the permanent magnets in present market can only provide a maximum field about ∼ 20  kOe. This fact indicates that a large MCE under low magnetic field change is desirable for the fulfillment of a magnetic refrigerator. Low magnetic field induced giant magnetic entropy change has been observed in some rare-earth based intermetallic compounds, such as ErMn₂Si₂, ^[5]ErCr₂Si₂, ^[6] ErRu₂Si₂, ^[7]HoCuSi, ^[8] ErFeSi, ^[9] and TmGa, ^[10] whereas it has not been observed in rare-earth oxides. Alternatively, magnetic refrigeration can also be achieved by a rotating field MCE based on changing the magnetic anisotropy energy in a constant magnetic field, ^[11] which is attractive due to the simplification and possible miniaturization of the device.^[12] Recently, rotating field entropy change due to magnetocrystalline anisotropy has been observed in TbMnO₃, TmMnO₃, ErFeO₃, HoMn₂O₅, and PrSi at low temperatures.^{[13– 17]} The exploration of magnetic refrigerant materials with large anisotropic MCE under low magnetic field has practical application value.

In the present work, we report a detailed study on the low-field MCE of DyFeO₃ single crystal around liquid helium temperature. The reason for choosing DyFeO₃ single crystal is three-fold. Firstly, DyFeO₃ shows a complex magnetic transformation. In this system, iron ions order in a weakly canted antiferromagnetic structure below the Né el temperature T_N= 645  K, and exhibit characteristic spin-reorientation (Morin) transitions Γ ₄(G_x, A_y, F_z) → Γ ₁(A_x, G_y, C_z), ^{[18– 21]} at T_M∼ 50  K upon cooling, ^[22] which is only observed in DyFeO₃ within RFeO₃ (where R is rare-earth elements) series.^[21] The Dy^{3 +} sublattice remains paramagnetic until the temperature reaches its ordering temperature 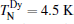. 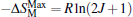The multiferroic, magnetoelectric properties together with the superfast optomagnetic effect of DyFeO₃ single crystal have been extensively investigated.^{[20, 23– 25]} Unfortunately, the effect of the interaction between the two magnetic sublattices on the MCE has not been understood yet. Secondly, the magnetic moment of Dy^{3 +} ion is large, and consequently a large magnetic entropy change can be expected in DyFeO₃ single crystal according to the relation of , where R is the gas constant, and J is the total angular momentum of the magnetic ion. Finally, owing to the strong magnetocrystalline anisotropy, a giant magnetic entropy change along the b axis of DyFeO₃ single crystal at 20  kOe around the ordering temperature of Dy^{3 +} is observed. This discovery not only advances our understanding of the MCE anisotropy in the DyFeO₃ single crystal, but also opens a new arena for magnetic refrigerator by rotating its magnetization vector at a relatively small magnetic field, instead of moving it in and out of the magnet.

DyFeO₃ ceramic was prepared with the starting material Dy₂O₃ (> 99.9%)and Fe₂O₃ (> 99.9%) by using the solid-state reaction method, and was pressed into pellets and sintered in air atmosphere for 48  hours at 1300  ° C. The crystal structure of the sample was examined by powder X-ray diffraction. Seed rods for crystal growth were prepared under the hydrostatic pressure and sintered at 1400  ° C for 48 hours in air atmosphere. DyFeO₃ single crystal was grown with four ellipsoidal mirrors (Crystal Systems Inc, FZ-T-10000-H-VI-VP) by the floating zone method. Back-reflection Laue X-ray diffraction experiments were carried out to check the single crystallinity and determine the crystallographic direction. Measurements of magnetization as functions of temperature and magnetic field were performed on commercial superconducting quantum interference device (SQUID) magnetometer (quantum design MPMS-XL).

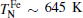
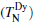
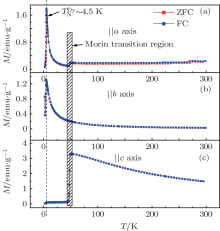XRD patterns and back-reflection Laue XRD patterns (not shown) confirmed that DyFeO₃ single crystal has an orthorhombically distorted pervoskite structure with Pbnm symmetry, which presented a high single crystallinity of the studied crystals. The Fe magnetic sublattices undergo a paramagnetic-antiferromagnetic transition around .^[26] Below the transition temperature, the configuration of Fe  magnetic sublattice is Γ ₄(G_x, A_y, F_z), in which the G-type component directly toward the a axis (G_x), but with a canting angle away from the a axis, which causes A-type and weak ferromagnetic (WFM) components along the b and c axis.^[23] Figures  1(a)– 1(c) show the tempareture dependence of zero-field cooling (ZFC) and field cooling (FC) magnetizations measured in H= 100  Oe from 2  K to 300  K for the DyFeO₃ single crystal along the a, b, and c axes, respectively. We can see an obvious decreasing magnetization along the c axis from 50  K to 45  K, which is followed by a continuous reorientation (Morin) transition from the c to the a axis, corresponding to the spin reorientation of Fe^{3 +} moments from Γ ₄(G_x, A_y, F_z) configuration to Γ ₁(A_x, G_y, C_z) configuration.^[22] The spin reorientation of DyFeO₃ is contrary to the case of other rare-earth orthoferrites which show a reorientation transition from Γ ₄(G_x, A_y, F_z) to Γ ₂(F_x, C_y, G_z).^[21] On further cooling, the kink point at 4.5  K indicated by the dotted line of Figs.  1(a) and 1(c) corresponds to the ordering of Dy^{3 +} moments .

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Zero-field-cooled (ZFC) and field-cooled (FC) thermal magnetization curves of DyFeO3 along the (a) a, (b) b, and (c) c axes from 2  K to 300  K under a magnetic field of 100  Oe.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Isothermal magnetization curves of DyFeO3 single crystal. (a) Magnetization curves along the a axis, (b) magnetization curves along the b axis, (c) magnetization curves along the c axis. The curves at 2  K and 4  K for the b axis are shown in the inset (b) for clarity.

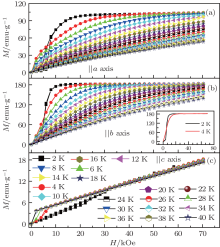
The isothermal magnetization curves as functions of field along different crystal directions were measured to investigate the anisotropic magnetic entropy change in DyFeO₃ single crystal. Figures  2(a)– 2(c) illustrate the isothermal magnetization curves along the a, b, and c axes of the DyFeO₃ single crystal in the temperature range of 2– 40  K with an interval of 2  K, respectively. The isothermal magnetization curves along the a and c axes of the DyFeO₃ single crystal in the Fe^{3 +} moments spin-reorientation temperature range of 40– 70  K are also measured (not shown). There is no obvious increase or peak in the curves. This is because the magnetization change in the Morin transition region is quite small since the magnitude of the WFM component is about 0.01 percent of the G-type component in an Fe sublattice. The magnetization curves for these three directions are different either in shape or in magnetization values. A spin-flip phenomenon can be observed along the a, b, and c axes of the DyFeO₃ single crystal at 2  K due to the antiferromagnetic interaction of R– R being similar to TbFeO₃.^{[27– 29]} A complete reversibility of MCE requires that no hysteresis of either the temperature or the magnetic field appears in the vicinity of a magnetic ordering temperature. As shown in the inset of Fig.  2(b), a negligible hysteresis loop was observed only at 2  K and 4  K for the b axis. When the temperature is above 4  K, no hysteresis loops can be observed from the isothermal magnetization curves. From the data we can see a significant difference in the isothermal magnetization curves along the a, b, and c axes of the DyFeO₃ single crystal, especially between the b axis and the c axis at low field, which implies that a giant anisotropy of MCE can be expected in the bc plane. Magnetic field-induced entropy change -Δ S_M was calculated from the isothermal curves with the following equation based on a Maxwell relation:

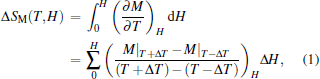
where the slope of two adjacent data points is approximatively used for the numerical calculation of the gradient of (∂ M/∂ T)_H. In this case, Δ T = 1  K and Δ H = 2  kOe.

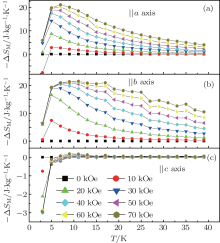
The calculated -Δ S_M as a function of temperature is shown in Figs.  3(a)– 3(c) for a field along the a, b, and c axes, respectively. Peaks appear at 9  K for the a axis with a value of 21.10  J/kg· K and at 11  K for the b axis with a value of 21.48  J/kg· K in a field of 70  kOe, whereas the values of -Δ S_M for the c axis are smaller than those of the other two axes in the temperature range above the ordering of Dy^{3 +} moments . We can clearly see a giant entropy change with a value of 16.51  J/kg· K along the b axis in a low magnetic field of 20  kOe near the ordering temperature of Dy^{3 +} moments. Furthermore, a large anisotropy of the MCE is observed in the DyFeO₃ single crystal along the b axis and c axis driven by a low magnetic field. The temperature of the corresponding peaks along the b axis of DyFeO₃ single crystal is close to the magnetic transition of a Dy sublattice, which implies that Dy– Dy interaction plays an important role in giant MCE in a low magnetic field.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Magnetic entropy changes of DyFeO3 single crystal. (a) Magnetic entropy changes along the a axis, (b) magnetic entropy changes along the b axis, and (c) magnetic entropy changes along the c axis.

Fig.  4.

	Figure Option ViewDownloadNew Window
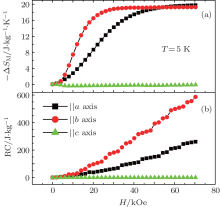	Fig.  4. Calculated -Δ SM and refrigeration capacity (RC). Field dependence of (a) magnetic entropy changes of DyFeO3 and (b) refrigeration capacity along the a, b, and c axes at 5  K.

The field-dependent -Δ S_M of different axes of DyFeO₃ single crystal at 5 K is shown in Fig.  4(a). A large anisotropy of MCE is observed in DyFeO₃ single crystal among the ab plane and c axis. It is noteworthy that there is a giant change below 20  kOe along the b axis at 5  K. For magnetic refrigeration application, not only a large entropy change value, but also a large refrigeration capacity is needed. The characteristic parameter that determines the magnetic cooling efficiency of a magnetocaloric material is the refrigeration capacity (RC) and is defined as

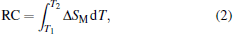
where T₁ and T₂ are the temperatures corresponding to both sides of the half-maximum value of -Δ S_M peak. The RC is the measurement of the amount of heat transfer between the cold and hot reservoirs in an ideal refrigerator as a function of field. The field-dependent refrigeration capacity of different crystallines of the DyFeO₃ single crystal is shown in Fig.  4(b). The three directions of DyFeO₃ single crystal manifest obvious anisotropy with RC value, which is equal to 260.48  J/kg, 586.08  J/kg, and 10.1  J/kg in a field of 70  kOe for a, b, and c axes, respectively. It is interesting that DyFeO₃ single crystal exhibits a strong magnetocrystalline anisotropy between b and c axes. Single crystal with giant anisotropic MCE at a relatively small magnetic field is a promising choice for the new type of magnetic refrigeration by simply rotating the magnetic field or refrigerants.

Fig.  5.

	Figure Option ViewDownloadNew Window
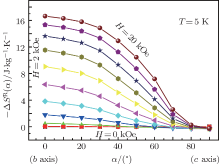
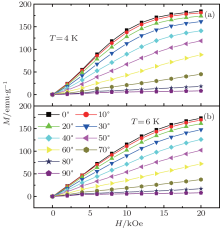	Fig.  5. Isothermal magnetization curves within the bc plane of DyFeO3 single crystal at (a) 4  K and (b) 6  K. 0° and 90° correspond to the direction of b and c axes, respectively.

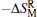
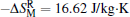
The rotating magnetic entropy change can be obtained by rotating the crystal from the b axis to the c axis and measuring the corresponding isothermal magnetization curves. The representative isothermal magnetization curves at different angles for temperatures of 4  K and 6  K for DyFeO₃ single crystal in the magnetic field range of 0– 20  kOe with an interval of 1  kOe are shown in Figs.  5(a) and 5(b), respectively. Taking the b axis as the initial angle, we can obtain the rotating magnetic entropy change as a function of angle by using Eq.  (1). As shown in Fig.  6, the largest values of under 20  kOe can be achieved at temperature of 5  K for DyFeO₃. The large reversible anisotropic magnetic entropy change at a relatively small magnetic field suggests that a promising candidate for new type magnetic refrigeration can be achieved at low field. Low-field-induced giant anisotropic magnetocaloric effect can be realized in the practical application by simply rotating the DyFeO₃ single crystal or magnet, rather than moving the magnetic refrigerant in and out of the magnet.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Rotating field entropy changes -Δ SR(α ) from the b axis to the c axis versus magnetic field DyFeO3 single crystal at 5  K.

In conclusion, a large anisotropic entropy change and RC were observed in DyFeO₃ single crystal. Owing to the strong magnetocrystalline anisotropy between b and c axes, there was a giant rotating magnetic entropy change under 20  kOe at 5  K. This discovery not only gives us a deeper insight into the understanding of the MCE anisotropy in spin canting anti-ferromagnetic single crystal, but also moves forward the practical application for rotary magnetic refrigerator by rotating its magnetization vector at a relatively small magnetic field, instead of moving it in and out of the magnet.