Recently, reversible resistive switching (RS) in metal/oxide/metal sandwiched structures has attracted great attention due to its potential for making high performance resistance random access memories (RRAM).^{[1– 5]} By applying voltage pulses, the resistances of the devices can be reversibly switched between nonvolatile high resistance state (HRS) and low resistance state (LRS).^{[1, 2]} The formation/rupture of the conductive filaments in the oxide matrix is one of the usual ways to realize this RS behavior.^[1] For many freshly fabricated RRAM cells, a forming process, in which a forming voltage (V_form) develops initially conductive filaments inside the insulator layer, is usually needed to active the memory cell before the memory cell can work. Then, a reset process, in which a reset voltage (V_reset) ruptures the filaments, switches the cell from LRS to HRS. Next, another set voltage (V_set) re-captures the filaments and switches the cell from HRS to LRS again, which is denoted as the set process. During the forming and the set processes, a compliance current is used to limit the possible big avalanche current to avoid damaging the memory cell.

Many experimental and theoretical investigations have reported that conductive filaments can be formed/ruptured by the redox of metal ions and/or the migration of oxygen vacancies in the oxide matrix.^{[1– 3]} This ion-migration-related filament-type switching mechanism usually has good retention, high off/on ratio, and nanosecond-scale switching speed. However, the random formation/rupture of filaments at non-controllable local regions usually leads to large fluctuations on both the endurances and the critical switching voltages, which greatly hinders the actual memory applications.^{[1– 3]}

Alternatively, the voltage can form/rupture filaments by changing and/or reshaping the metallic electronic phases in strongly correlated electron systems without long-range migration of the ions/vacancies.^{[4– 6]} This mechanism, if applicable, would offer a highly favored advantage in terms of switching speed because electron hopping is much faster than ionic migration. As one of the most investigated electron phase separated manganites, (La_{1− y}Pr_y)_{1− x}Ca_xMnO₃ displays a first-order electronic phase transition between ferromagnetic metallic (FMM) and charge-ordered insulating (COI) phases, and exhibits wide liquid-like and frozen phase separation (PS) temperature regions, in which the external stimuli can easily tune the transport behavior of the system.^{[7– 11]} A small voltage or current reshapes the FMM phase domains, and finally leads to the formation of conductive filaments along the electric field direction by the intrinsic electronic effect.^{[6, 12– 16]} However, with a large electric field applied, the remarkably parasitic Joule heating in the filament regions can dramatically increase the temperature in the local regions.^{[4, 6]} Due to the first-order electronic phase transition nature, the Joule heating induced local annealing of the system would result in different frozen PS structures and lead to different nonvolatile resistance states at low temperature.

Since the first-order electronic phase transition can be well controlled by both the electric field and the annealing processes, the resistive switching based on such a mechanism in electronically PS manganites should be more stable than that based on the non-controllable ion-migration mechanism. The stable RS behavior based on the electronic phase transitions in La_0.225Pr_0.4Ca_0.375MnO₃ has been experimentally presented in earlier investigations.^{[4, 12]} However, in such an electronic phase transition switching mechanism, the Joule heat annealing usually needs a large current and has a long relaxation time (in tens of seconds time scale), which means large energy consumption and long operation time, respectively. Since the parasitic Joule heating effect is ignored in the Monte Carlo simulations, the electric field with a fixed direction can form the FMM filaments but cannot rupture them.^[13] To solve this problem, we suggest a three-terminal memory device based on La_0.225Pr_0.4Ca_0.375MnO₃ and study the reversible RS using Monte Carlo (MC) simulations based on the dielectrophoresis model. Our result indicates that by reshaping the FMM domains, the conductive filaments can be formed and annihilated by two cross-oriented switching voltages, respectively. With this controlling protocol, large Joule heating can be avoided, and the switching voltage and the switching time can be effectively reduced.

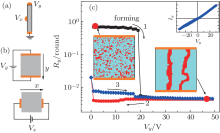
Figure 1(a) shows a schematic drawing of the 3-terminal device. The device is set (from HRS to LRS) by a vertical voltage V_y and reset (from LRS to HRS) by a horizontal voltage V_x. The resistances of the device are read via the V_y terminal, i.e., the HRS or LRS states are determined by the y-direction resistance R_y. To model the electronically PS structure, we start from a two-dimensional square lattice (L × L, L = 50), where each bond represents an electronic phase (FMM or COI). Therefore, this lattice is more or less a coarse-grained model of the realistic PS structure in (La_{1− y}Pr_y)_{1− x}Ca_xMnO₃. As shown in Fig. 1(b), the voltage V_y is applied in the y direction to form conductive paths, while the voltage V_x is applied along the x direction to annihilate the filaments, which is equivalent to the 3-terminal configuration in Fig. 1(a).

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) Schematic drawing of the 3-terminal memory device. (b) Illustration of the device configurations during the simulation processes. (c) The Vy dependent y-directional resistance Ry. The top-right inset shows the Iy– Vy behavior after the forming process. Left and bottom insets are the snapshots of PS at the initial and the final states, respectively. Red and cyan sites represent the metallic and the insulating phases, respectively.

In our MC simulation, a standard Metropolis algorithm is used with a dielectrophoresis mechanism. Considering the fact that the conversion between FMM and COI phases can be ignored after the application of a low electric field (< 10⁶ V/m), the fixed fraction (p_M) of “ flowable” FMM phase sites in the insulating matrix can describe the PS structure in manganites.^{[12, 13, 17]} The exchange between the nearest neighboring (NN) lattice sites is proportional to the probability determined by the free energy change. The total free energy can be written as^[13]

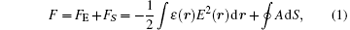
where F_E denotes the electric energy; the dielectric constant ε (r) equals ε _M(r) or ε _I(r) when r locates in the metallic phase or the insulating phase, respectively; and, F_S represents the interface energy between metallic and insulating phases, and is proportional to the interfacial area S with a coefficient A. The local field E(r) and the resistance R_y along the y direction can be calculated using the resistor-network (RN) model, ^{[18– 20]} in which three types of resistors are distributed according to the bonds (links) between the NN sites: R_M between metallic sites, R_I between insulating sites, and R_MI between a metallic site and an insulating site. For simplification, we have R_MI = (R_M+ R_I)/2 here.^[20] The voltage at each site V(r) is obtained by solving the Kirchhoff equations and E(r) is the negative gradient of V(r). To accelerate the calculation the R_I/R_M ratio and the ε _M/ε _I ratio are assumed to take the same value f (≫ 1). The simulation is performed at a fixed temperature. The parameters used in our simulation are listed in Table 1. The system evolves as time passes, e.g., Monte Carlo steps (MCS).

Table 1.

Table 1.

Table 1. The parameters used in the model. Here, the selection of pM, which is within the reasonable range (Ref. [11]), mostly benefits the RS and can lead to the smallest switching times during the filament forming/rupture processes. The value of f is within the experimental range for manganites (Refs. [4] and [8]). The other parameters are relative values. pM ε I T A f 18% 2 1.0 0.85 3× 103

Table 1. The parameters used in the model. Here, the selection of pM, which is within the reasonable range (Ref. [11]), mostly benefits the RS and can lead to the smallest switching times during the filament forming/rupture processes. The value of f is within the experimental range for manganites (Refs. [4] and [8]). The other parameters are relative values.

In the vertical direction, the V_y-dependent resistance R_y is shown in Fig. 1(c). The left inset in Fig. 1(c) shows the initial HRS state, in which the metallic sites (red regions) are distributed randomly in the insulating matrix (cyan regions). With the increase of V_y from zero, R_y first remains at the HRS, then dramatically drops to an LRS at V_y ∼ 20, and finally keeps at the LRS even when V_y ∼ 50, being qualitatively consistent with the previously experimental results.^{[6, 12]} The lower right inset in Fig. 1(c) shows that the metal phase domains have been reshaped by V_y and aligned into the conductive filaments along the y direction as V_y ∼ 50. Hence, the forming of the filaments explains the dramatic drop of R_y at V_y ∼ 20. Next, as V_y is retracted from 50 to 0, and then re-increased to 50, R_y always remains at the LRS, indicating that the V_y-induced resistance switching is nonvolatile. In addition, the Ohmic I_y– V_y behavior in the upright inset of Fig. 1(c) shows that the resistance of the LRS is almost V_y-independent, even with reversing the polarity of V_y.

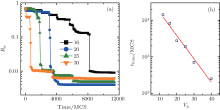
Due to the existence of a remarkable aging effect in PS manganites, the resistance of the system also strongly depends on the dynamic evolution history.^[9] Here, we simulate the time dependent R_y under the stressing of different V_y. For the different V_y situations, the simulations all start from the same initial HRS state. Figure 2(a) shows the time dependent R_y behaviors with V_y = 30, 25, 20, and 16 respectively. With initial V_y = 30, V_y suddenly drops to the LRS in a forming time t_form = 680 MCS. With the decrease of V_y, the suddenly drop of resistance still appears but t_form increases exponentially, as shown in Fig. 2(b), which is consistent with a dynamic percolation scenario.^{[6, 12, 14]} Hence, the time needed for forming the conductive filament is determined by the amplitude of V_y.

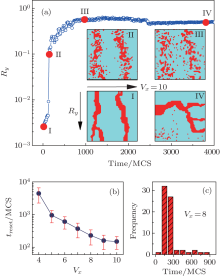
On the other hand, to annihilate the y-direction filament and switch the system back to the HRS, we apply a constant voltage V_x = 10 along the x direction and then calculate R_y. The time dependent R_y and the snapshots of PS at t = 0, 140, 1000, and 3800 (MCS) are shown in Fig. 3(a) and the insets, respectively. At the beginning of applying V_x, the filaments along the y direction remain and R_y stays at the LRS. With the lapse of time, the filaments start to be dissolved and R_y displays a dramatic jump to a high value at a critical time, i.e., the reset time t_reset = 140, and then continues with a small increase until t = 1000, obtaining the stable HRS. With further increase in the evolution time to above 3800 MCS, the y-direction filaments are completely dissolved while the filaments along the x direction come into being on the contrary. Therefore, the LRS can be reset to the HRS by applying a voltage along the x direction with enough time.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The forming process. (a) Time dependent Ry under the stressing of different Vy. (b) The Vy dependent forming time tform. Here tform is defined as the time when a dramatic resistance drop occurs.

Besides, in the reset process from LRS to HRS, t_reset strongly depends on the value of V_x. To reveal this relationship, we simulate and calculate the time dependent R_y under the stressing of different V_x. The simulation and calculation are repeated 69 times for data reliability. Figure 3(b) indicates that t_reset quickly decreases with increasing V_x. This is a reasonable result since the larger V_x can provide a larger dielectrophoresis force to disrupt the y-directional filaments. Figure 3(c) shows the count distribution of t_reset at V_x = 8. The distribution indicates that t_reset is usually between 150 and 250 (MCS) in the 1000 MCS simulations, which evidences the reliability of the data in Fig. 3(b).

For actual applications, it is beneficial to reset the device from LRS to HRS within a short time and by a small voltage. For the reset process in Fig. 3(a), t_reset ∼ 150 MCS and hence the usage of t = 1000 MCS is long enough to obtain a stable HRS. At this HRS, the y-directional filaments are ruptured but the metallic domains still mainly distribute in the regions nearby the previous filaments. To study how such HRS affects the next following switching from HRS to LRS, we again apply V_y = 16 in the vertical direction and calculate the time-dependent R_y.

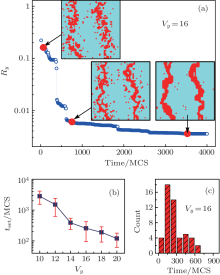
The simulation results, shown in Fig. 4(a) and its insets indicate that the disrupted filaments are re-captured and the system is set to the LRS again after a proper time, which is similar to the forming process shown in Fig. 2(a). However, one can easily find that the t_set needed for re-capturing the filaments is only ∼ 620 MCS, which is much shorter than t_form (t_form ∼ 8200 MCS) in Fig. 2(a). This suggests that, by controlling the HRS to a stable state just after the filaments are ruptured, the re-capture of the filaments becomes much easier and t_set is remarkably reduced.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The reset process. (a) The calculated Ry as a function of time, with the stressing of Vx = 10. The insets are four snapshots of the PS states at different times. (b) The Vx dependent reset time treset. (c) The count distribution of treset at Vx = 8, with 69 repeated simulations.

We have also studied the V_y-dependent t_set. The simulation starts from an HRS state with the PS structure shown in the left inset of Fig. 4(a), and is carried out by monitoring the evolution of the PS structure under the stressing of different V_y. Figure 4(a) indicates that t_set also decreases with increasing V_y, which is similar to the dependency of t_reset with V_x. By comparing the forming processes under different situations shown in Fig. 2(b), one can easily find that t_set is always smaller than t_form whatever V_y is. Figure 4(c) shows the count distribution of t_set in the 51 repeated simulations within 1000 MCS at V_y= 16, in which t_set < 700 MCS and is mainly distributed between 150 MCS and 250 MCS.

Therefore, the switching time can be reduced by increasing the switching voltage and can be further reduced by choosing a proper HRS. According to this result, one can select suitable forming, set, and reset voltages to produce the reversible RS between stable HRS and LRS within 1000 MCS. To verify this conclusion, we simulate the continuously reversible RS that starts from the initial HRS state shown in the left inset of Fig. 1(c). To obtain the conductive filaments from the initial HRS state within 1000 MCS, V_y = 30 is used as the forming voltage. In the simulation, V_y = 16 and V_x = 8 are used as the set and the reset voltages, respectively, and they are alternatively applied to the device with a fixed duration of 1000 MCS.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The set process. (a) The calculated Ry as a function of time, with the stressing of Vy = 16. The insets are three snapshots of the phase separation states at different times. (b) The Vy dependent set time tset. (c) The count distribution of tset at Vy = 16, with 51 repeated simulations.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Time dependent reversible resistive switching with alternative applying Vx and Vy pulses respectively. The pulse durations are fixed to 1000 MCS.

Figure 5 shows the simulation result, in which the continuously reversible and stable RS is clearly displayed. It needs to be addressed that both the HRS and the LRS are stable and have good retentions after the turn-off of the set and the reset voltages since the PS state in manganites below ∼ 30 K is frozen.^[6]

Our simulation results indicate that applying larger operation voltages V_x and V_y can effectively reduce the switching times, including t_set and t_reset. In the actual memory application, however, a large operation voltage not only leads to a large energy consumption but also produces remarkable Joule heating that would extend the switching time and weaken the RS stability on the contrary. This happens because the Joule heating induced increase of temperature would lead the system into a liquid-like PS state with a much more remarkable aging behavior, even though no external voltage is applied.^[9] Therefore, the Joule heating limits the maximum applicable operation voltages.

It can be imaged that the operation voltage and the switching time are also dependent on the sizes of the system. The previous investigation has revealed that the FMM filaments in (La_{1− y}Pr_y)_{1− x}Ca_xMnO₃ can be formed in the nanometer scale.^[21] A sample device with a size of a hundred-nanometers can be designed to effectively reduce the number of filaments inside the device. In such a small device, by assuming that the electric field intensity for resistive switching is fixed, the few filaments with nanometer scale size greatly reduce the switching voltages. By using the parameters taken from the experiments, ^{[4, 5, 11, 12]} the resistivity of the filament is calculated to be ρ ∼ 10⁴ Ω · m, and the critical electric field that forms the filament in Fig. 1(c) is estimated to be E_c ∼ 10³ V/m. By assuming that the device size is l = 100 nm and the filament formed inside it has a diameter of d = 20 nm, it can estimated that the switching voltage V_c = lE_c ∼ 10^{− 4} V and the heating power 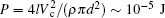. Such small switching voltages and heating powers suggest that the device is energy conservation and Joule heating can be neglected. In addition, it needs less time to “ move” or reshape the FMM domains to capture or rupture the nanometer-scale filaments. Thus, the switching time can be also greatly reduced in the nanometer-scale device.

We have studied the resistive switching of a 3-terminal device based on the electric phase separation manganites by using Monte Carlo simulations with the dielectrophoresis model. Our result indicates that the conductive filaments can be formed and annihilated by two cross-oriented switching voltages V_y and V_x, respectively. By using this control, the reversible and stable resistive switching between HRS and LRS is demonstrated. Our simulation also indicates that both the set and the reset times decrease with increasing switching voltages. Besides, by controlling the HRS to a stable state just after the rupture of the conductive film, both the switching voltages and the switching times can be further reduced. Based on the PS manganites, a nanometer-scale 3-terminal device is suggested to produce a high performance resistive switching behavior.

The electrical modulation of the electronic metal phase is an important mechanism for reliable resistance switching because the electronic migration is much faster than the ionic migration. We believe that the electrical modulation of the electronic metal phase is a general mechanism and should be observed in many electronic phase-separated oxides. With this electronic switching mechanism, we believe that the method with two cross-oriented switching voltages can be applied to realize reversible resistance switching between HRS and LRS in many oxides.