†Corresponding author. E-mail: fshuang@iim.ac.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61203061 and 61074052), the Outstanding Young Talent Foundation of Anhui Province, China (Grant No. 2012SQRL040), and the Natural Science Foundation of Anhui Province, China (Grant No. KJ2012Z035).
Recent studies show that quantum non-Gaussian states or using non-Gaussian operations can improve entanglement distillation, quantum swapping, teleportation, and cloning. In this work, employing a strategy of non-Gaussian operations (namely subtracting and adding a single photon), we propose a scheme to generate non-Gaussian quantum states named single-photon-added and -subtracted coherent (SPASC) superposition states by implementing Bell measurements, and then investigate the corresponding nonclassical features. By squeezed the input field, we demonstrate that robustness of non-Gaussianity can be improved. Controllable phase space distribution offers the possibility to approximately generate a displaced coherent superposition states (DCSS). The fidelity can reach up to F ≥ 0.98 and F ≥ 0.90 for size of amplitude z = 1.53 and 2.36, respectively.
In recent years, considerable theoretical and experimental investigations have been focused on preparing non-Gaussian optical states due to their strongly nonclassical properties, such as entanglement and negativity of the quasi-probability phase-space distributions, which are important for the efficient implementation of quantum information and communication protocols, [1– 5] quantum estimation tasks, [6, 7] and quantum cloning.[8] However, due to higher-order optical nonlinearity limitation, achieving much higher non-Gaussianity of the radiation field is a considerable challenge.
Based on non-Gaussian operations (i.e., photon addition and subtraction), Ourjoumtsev et al. have presented a detailed experimental analysis of kitten state generation by subtracting one photon from a squeezed vacuum beam.[9] Reference [10] reported a scheme to generate squeezed superpositions of coherent states. However, highly non-Gaussian states preparation need to subtract more photons and this leads to a rapid decrease of generation fidelity and success probability. Another alternative approach is to take advantage of the effective nonlinearity induced by conditional measurements[11] and feedback control.[12] These kinds of measurement-induced control strategies have taught us something about systematic approaches of quantum states generation and the qualitative role of quantum coherence and entanglement between the interested system and measuring equipments.[10, 13, 14] By virtue of conditional measurements, Lvovsky and Mlynek[15] first introduced a so-called “ quantum optical catalysis” method to prepare coherent superposition states (CSS). This scheme exhibits higher fidelity only for very small amplitude state preparation. Various control strategies have been proposed for the non-Gaussian states preparation, such as photon-added and photon-depleted states, [16] photon annihilation-then-creation and photon creation-then-annihilation thermal states, [17] photon-added two-mode squeezed coherent states, [18] arbitrary superposition of zero- and one-photon, [19] odd photon number superposition state, [20] photon-subtracted squeezed states, [21] and the Schrö dinger cat state.[14, 22– 24]
At present, it is an urgent task to prepare larger-size non-Gaussian states with high fidelity. However, the usual optical resonant cavity is a linear amplifier, which cannot be applied to prepare large-size non-Gaussian states. Noiseless amplification methods[25, 26] can work well only for small-size quantum states preparation. Based on the optical interference, Takahashi et al. have demonstrated a novel way to enhance the size of CSS.[27] The preparation fidelity would approximate > 90% for | α | 2 = 1.2 and 2.0 ideally, while the values are 76% and 60% in the experiment. Very recently, based on quantum optical catalysis mentioned above, Bartley et al. investigated the multi-photon quantum states engineering and generated a weak DCSS (α = 0.9) with > 90% fidelity.[28]
In this work, by implementing non-Gaussian operations and Bell measurements, we propose a scheme to generate superposition states, the so-called single-photon-added and single-photon-subtracted coherent (SPASC) superposition states. Instead of subtracting more photons, we show that squeezing the input field can enhance non-Gaussianity. In phase space, the quasi-probability distributions of the single-photon-added and -subtracted squeezed coherent (SPASSC) superposition states exhibit a close approximation to that of a displaced coherent superposition states (DCSS). This will provide possibilities to achieve DCSS with higher fidelity. Therefore, we arrange our work as follows. In Section 2, relying on the simple optical elements, we briefly introduce the realization of non-Gaussian operations, namely adding (subtracting) one single photon to (from) Gaussian-like field. Then we propose a conceptual experiment apparatus for preparing SPASC superposition states and investigate the negativity of its Wigner function and non-Gaussian features. In Section 3, in order to enhance quantum non-Gaussianity, we consider a squeezed incident field and demonstrate that squeezing can improve the robustness of quantum non-Gaussianity. As an application, in Section 4 we show that DCSS can be approximately prepared by generating and manipulating SPASSC superposition states, and we then obtain the optimal fidelity. Some conclusive remarks will be made in Section 5.
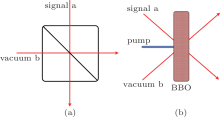
As one of the most commonly linear unitary devices, a beamsplitter (BS) is often employed to prepare quantum states. Most generally, under the boson realization, a lossless BS can be described as B̂ = exp [θ (ab† − a† b)] , where θ is related to the reflectivity R = sin2θ . For a high transmission beamsplitter (HT-BS), the reflectivity is low enough (θ ≪ 1), and we can see

where | ψ 〉 1 denotes the input optical field, annihilation operator a subtracts one single photon from the incident mode a, and creation operator b† adds one single photon to the vacuum mode b (detailed in Fig. 1(a)). In fact, this acts as an entangler. If single-photon counting measurement (e.g., avalanche diode detector) was performed upon mode b, then the output signal states depend on the results of the conditional measurements.
Reflectivity θ ≪ 1 means that a one-single-photon output in vacuum mode b is only a small minority. At the same time, the output signal field collapses to a single-photon-subtracted state | ψ , − 1〉 1. Considering a low enough coherent state (| α | ∼ 1), the output is very close to the Yurke state.[29] The nonclassicality and decoherence of a photon-subtrated-squeezed field in a thermal environment have been investigated.[30, 31]
A nonlinear crystal with weak nonlinear interactions is an important source to produce a single photon. A parametric down-conversion (PDC) process splits a pump photon into two photons that obey the global energy and momentum conservation laws, and the emitted photons are highly quantum correlated. In principle, this twin-photon generating process can be described by T̂ = eg(a† b† − ab), where g is the parameter gain of χ (2) nonlinearity, mainly determined by the crystal size, components, temperature, pump power, etc. For lower gain, the output reads
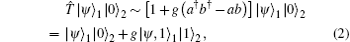
in which the creation operator a† acts upon the input field mode a and then a single photon emits from the idler mode b. The single-photon-added state can be prepared by heralded detecting one single photon on the idler mode b (as shown in Fig. 1(b)). Similar to the photon-subtracted field, the photon-added field can also unveil the nonclassical features. Reference [32] has reported the experimental generation of single-photon-added coherent state to visualize the evolution of the quantum to classical transition, and witnessed the gradual change from spontaneous to stimulated regimes of light emission. More experimental details and applications of subtracting and adding photons processes can be found in Refs. [33]– [35].
A lower amplitude coherent field | α 〉 1 is injected into an HT-BS and then undergoes PDC process. The output can be written as
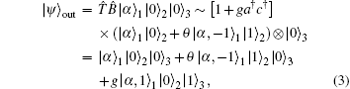
which is an entangled state. That is to say, the output is correlated with the vacuum and idler modes. It should be pointed out here that the higher-order nonlinear interactions are neglected in the above derivation. As is well known, quantum measurements are very different from classical measurements. Due to the probability of measurement outcomes, one may only obtain a state of maximal knowledge about a quantum system, not a state of complete knowledge. Moreover, quantum measurements backaction can result in state collapse onto a subspace that is spanned by the eigenvectors associated with the observable eigenvalues. If the measurement result is precisely known, then the final state will be uniquely determined. Hence, we name this kind of state preparation method as conditional generation, and the final state as the conditional state. In the traditional quantum projective measurements, the Bell measurement is the most popular. It has four projectors, namely,
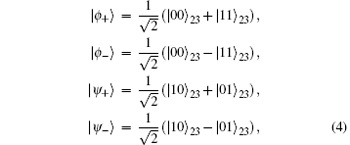
and 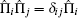
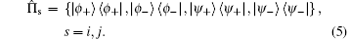
By performing Bell measurements upon modes 2 and 3, the signal field collapses to the desired state at mode 1.
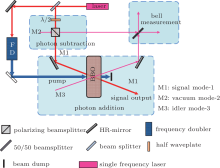
To apply the above-mentioned process to Eq. (3), a conceptual experimental apparatus is designed and shown in Fig. 2. After passing through a half waveplate (HWP) and a polarized beamsplitter (PBS) in turn, a small part of seed light emitted from a mode-locked single-frequency laser is injected to a high transmission beamsplitter (HT-BS), which annihilates one single photon from the input weak coherent field. The single-photon-subtracted coherent state is a small minority of the output field and the majority is the original coherent field. By injecting the output field into a type-I BBO crystal and mixing with a vacuum field, the pump photon splits into twin photons with the same linear polarization and frequency. In the nonlinear crystal, the parametric down-conversion (PDC) process adds one photon to the input field. Thus, single-photon-added coherent state is generated with a byproduct of single photon in idler mode.
By matching the two spatial modes in the Bell states at a PBS, the SPACS superposition states will appear in output port. These conditional states are given by
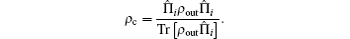
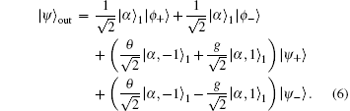
Based on the Fock filtering, [36] one can also distinguish four Bell states unambiguously from the measurement outcomes. Moreover, it is not very difficult to partially distinguish Bell bases in the experiments. Bell measurement results | ψ + 〉 and | ψ − 〉 indicate that the output state has collapsed to the SPASC superposition states, i.e.,
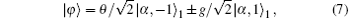
although in most cases the output signal contains the original seed coherent state. It is worth noting that ingredients of this superposition states are related to the parameters θ and g, which can be controlled by adjusting the HT-BS reflectivity and parameter gain.
In phase space, the Wigner function, which gives the most analogous description of quantum mechanics to classical statistical mechanics, is often employed to visualize nonclassical features of quantum states.[37, 38] For a quantum state, if there exists a negative part, then one can safely say that it is nonclassical. The Wigner function of the SPASC superposition states ρ out= | φ 〉 | 〈 φ | can be derived from W(x, p) = Tr[ρ outΔ (x, p)] , in which
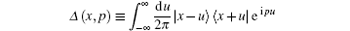
is the Wigner operator. Thus, we can derive the Wigner function of the SPASC superposition states as
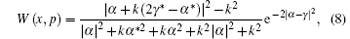
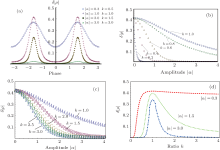
in which α is the amplitude of the input field, k = g/θ means the relative proportion parameter, and γ = x + ip denotes the coordinate variables of phase space. For a small-size input (| α | = 0.3), figure 3 shows nonclassical features of the SPASC superposition states with different values of k = 0.5, 1.5, and 3.0, respectively. With an increasing value of k, the partial negativity indicates that nonclassical features have been enhanced. This phenomenon is also observed in Figs. 4 and 5. By adjusting the half waveplate (HWP), temperature of the nonlinear BBO crystal, and pump power, one can adjust the reflectivity θ and the parameter gain g of parametric down-conversion (PDC) process to enhance nonclassicality.
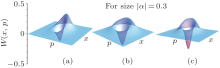 | Fig. 3. Wigner functions of the SPASC superposition states with fixed amplitude | α | = 0.3 and different relative proportion parameters k. (a) k = 0.5, (b) k = 1.5, (c) k = 3.0. |
In the case of | α | = 1.0, although the negative probability proportion can be enhanced by increasing value of k (as shown in Figs. 4(a)– 4(c)), this tendency has become very weak. When | α | = 1.5, raising k can only bring very mild nonclassical features. From Fig. 3 to Fig. 5, when increasing input intensity, we obviously see that the nonclassicality is ebbing.
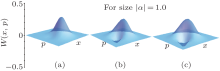 | Fig. 4. Wigner functions of the SPASC superposition states with fixed amplitude | α | = 1.0 and different relative proportion parameters k. (a) k = 0.5, (b) k = 1.5, (c) k = 3.0. |
In order to understand how the nonclassicality can be manipulated by the relative proportion parameter k and strength | α | , the non-Gaussianity of the SPASC superposition states have been investigated by introducing[39, 40]
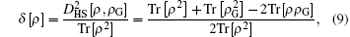
in which 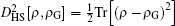
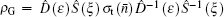
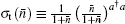

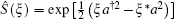

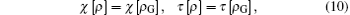
where χ [] and τ [ ] can be derived from
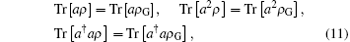
i.e., ρ G is the Gaussian state with the same covariance matrix and the same vector of the state ρ . Equations (10) and (11) decide the parameters
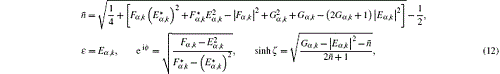
in which
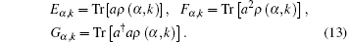
Considering Tr[ρ 2] = 1 and 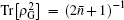
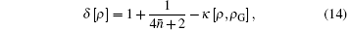
with
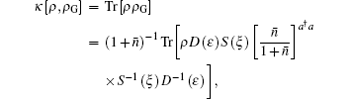
and with parameters from Eq. (12). The value of Eq. (14) ranges from 0 to 1, and larger value indicates stronger non-Gaussianity. Figure 6(a) tells us that δ [ρ ] is also dependent on the phase of input field. When taking values of the phase in the regions [− 2, − 1] and [1, 2], its non-Gaussianity is much stronger. For the maximum points, the phase takes ± π /2. For different input strengths, non-Gaussianity of the SPASC superposition states obviously decrease with raising strength | α | . This point can also be verified in Figs. 3– 5.
This superposition state is composed of two parts. The first is a single-photon-subtracted coherent state, which remains Gaussian. The second part, a single-photon-added coherent state, has the complete characterization of a non-Gaussian state as clarified by Zavatta et al. in Ref. [32]. In Fig. 6(b), by rising the value of k from 0.2 to 1.0, namely, amplifying the ratio of the single-photon-added coherent state, we can view that the corresponding non-Gaussianity can be strengthened. However, when k > 1, we visualize that its non-Gaussianity decreases with rising ratio (as shown in Fig. 6(c)). In Figs. 6(b) and 6(c), taking a smaller or larger values of k, we can see the corresponding non-Gaussianity is lower (see empty-circle points in Fig. 6(b) and alphabet “ E” points in Fig. 6(c)). If the value of k is around 1.0, the non-Gaussianity can be kept better than the other cases (empty-five-pointed star with k = 1.0 in Fig. 6(b) and alphabet A points with k = 1.0 in Fig. 6(c)). In Figs. 6(b)– 6(d) we also note that the peaks of the non-Gaussianity shall decrease with rising amplitude. This point can be understood by considering this process as a balance between the high non-Gaussianilty and large amplitude. Here it should be noted that, in order to obtain much higher non-Gaussianity quantum states, the phase of input field is limited in the above two regions, and in Figs. 6(b)– 6(d), the phases are − 1.4, − 1.4, and 1.5, respectively.
Figures 3– 5, 6(b), and 6(c) obviously show that non-Gaussianity heavily decreases with rising field intensity. This can be understood from two points: the absence of much stronger non-Gaussian operations and quantum noise. Namely, the added (subtracted) photon number is not greater than 1, and quantum noise covers the effect of non-Gaussian operations. In order to generate much higher amplitude non-Gaussian quantum states, adding (or subtracting) more and more photons or reducing quantum noise is feasible. Here instead of adding (subtracting) more photons, we squeeze the incident coherent field to realize noise reduction. For the case of a squeezed coherent field, we obtain a non-Gaussian single-photon-added and − subtracted squeezed coherent (SPASSC) superposition states and can improve the robustness of non-Gaussianity, while increasing the amplitude.
For a squeezed incident field, generated from Ref. [42], from Eqs. (1) and (2) the output is
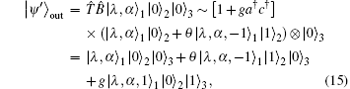
where | λ , α 〉 1 ≡ Ŝ (λ ) D̂ (α ) | 0〉 1 denotes a squeezed coherent field. After performing Bell measurements, the conditional states will be determined by the distinguishable measurement results. Therefore, we can generate the single-photon-added and − subtracted squeezed coherent (SPASSC) superposition states, namely,
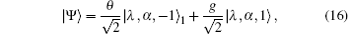
where | λ , α , − 1〉 1 ≡ a| λ , α 〉 1 means to subtract a photon from the squeezed coherent state, and | λ , α , 1〉 1≡ a† | λ , α 〉 1 means to add a photon. In contrast from this case (Eq. (7)), the single-photon-subtracted squeezed coherent state | λ , α , − 1〉 1 is a non-Gaussian one. Squeezing the field shall enhance the non-Gaussianity of the SPASSC superposition states. Obeying the same derivation procedures (Eqs. (10)– (13)), we have
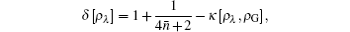
in which 
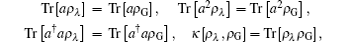
and ρ λ denotes the density matrix of the SPASSC superposition states in Eq. (16).
Figure 7 shows the non-Gaussianity of the SPASC (λ = 0) and SPASSC (λ = 0.2) superposition states for four different values of k. When the squeezing parameter value λ = 0.2, we find that its non-Gaussianity is robust against the amplitude rising. For various values of k, the sensibility of non-Gaussianity is different. According to the predictive mentioned in Section 2.4, a squeezing field can convert single-photon-subtraction coherent state to a non-Gaussian one. In order to interpret this point, we can utilize

to describe this process. The corresponding non-Gaussianity depends on the probability distribution of the photon-addition-coherent state, i.e.,
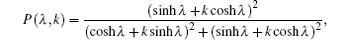
which is related with the squeezing parameter λ and ratio k. From its partial differential function 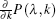
How to accurately and steadily generate target quantum states is a greatly important and indispensable step on the road to realizing quantum information processing. As a particular kind of non-Gaussian state, generating a coherent superposition states (CSS) has attracted some special attention due to their remarkable usefulness for universal quantum computation[43] and fundamental tests of quantum theories.[44– 46] DCSS can be defined as

where β is the displaced parameter, z denotes the amplitude of CSS, and the normalization constant N is
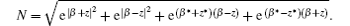
In phase space, its Wigner distribution function is shown in Fig. 8(a). Comparing Fig. 8(a) with Fig. 8(b), we can observe that the quasi-probability distribution features of DCSS are very similar to those of the SPASSC superposition states. In other words, the SPASSC superposition states can be controlled to approximately generate DCSS. Fidelity, which describes a distance measurement between an interested quantum state ρ and a given reference quantum state σ , can be defined as[47, 48]
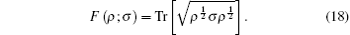
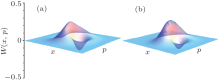 | Fig. 8. (a) Wigner functions of the displaced CSS with z = 0.9 and β = 0.7. (b) Wigner functions of the SPASSC superposition states with α = 0.4, λ = 0.8, k = 0.76 in Eq. (16). |
For the case of pure state (e.g., ρ = | Ψ 〉 〈 Ψ | , σ = | Φ 〉 〈 Φ | ), this definition can be simplified to be F(ρ ; σ ) = | 〈 Ψ | Φ 〉 | 2, which can be also called “ transition probability” . Suppose that DCSS is a reference quantum state with its amplitude z and displaced parameter β , we calculate the overlap squared between the states in Eqs. (16) and (17). Thus, we have
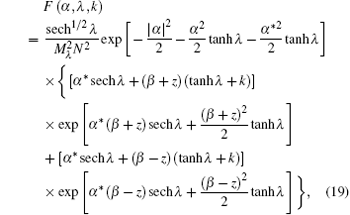
where Mλ is the normalization constant of ρ λ shown in Eq. (16).
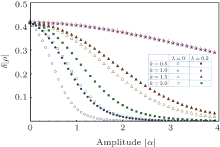
For | α | = 1.5 (here the phase is 1.05), the displaced parameter β = 0.9, by employing the above analytical expression shown in Eq. (19), we plot the behavior of the optimal fidelity of generating the target state for a range of coherent amplitude z (as shown in Fig. 9). It should be pointed out that, when taking λ = 0, equation (19) shows the fidelity of the SPASC superposition states with respect to the target DCSS. In the case of λ = 0, taking k = 1.045, the optimal fidelity is labelled by dotted line (red) with F = 0.703 for z = 1.1. Its tendency will rapidly decrease with increasing size of amplitude z. When taking λ = 0.307 and k = 1.050, we achieve the maximum fidelity F = 0.981 with z = 1.53 detailed by solid line (green). Then the fidelity will also decrease with increasing amplitude of DCSS. For λ = 0.559, k = 1.050, dashed line (blue) shows that the fidelity reduces to F = 0.906 with z = 2.36.
Employing the strategy of subtracting (adding) single photon from (to) the radiation field, we have proposed a scheme to generate the single-photon-added and -subtracted coherent (SPASC) superposition states by implementing Bell measurements, and investigated its nonclassical features by adjusting the reflectivity of the high transmission beamsplitter (HT-BS) and the gain of the parametric down-conversion (PDC) process. Instead of the original coherent light field, we utilize a squeezed field to reduce quantum noise and achieve the enhancement of quantum non-Gaussianity (e.g., the SPASSC superposition states), and then further demonstrated a better strategy to approximately generate the displaced coherent superposition states (DCSS) with higher fidelity by controlling the relative proportion parameter and the squeezing parameter. The experimental implementation of the distinguishable Bell measurements may be quite challenging, but our scheme does not need to subtract and add more photons. Actually, for a low-efficiency multiplexing avalanche photodiode (APD), this scheme remains useful. Its larger size and high fidelity indicates its possible applications to study quantum information processing and test the fundamentals of quantum theory.
The authors acknowledge the fruitful discussion about experimental setup with Prof. Guoyong Xiang and Chaoyang Lu, and their group members.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|