The attosecond pulse, as a powerful tool to trace and control the dynamics processes deep inside atoms and molecules, has opened a new time scale of the ultrafast electronic dynamics with unprecedented resolution.^{[1– 3]} Currently, one of the most successful ways towards achieving the attosecond pulse is through high-order harmonic generation (HHG) from the rare gases^{[4– 6]} that can be well understood by means of the classical “ three-step” model consisting of ionization, acceleration and recombination.^[7] Further, an attosecond pulse can be produced through superposing the harmonic spectrum in the supercontinuum region.^[8] Moreover, to generate the shorter attosecond pulse, many works have been done, such as the few-cycle driving pulse scheme, ^[9] the polarization gate scheme, ^{[10, 11]} the chirp pulse scheme, ^{[12, 13]} the two-color or multi-color pulses scheme, ^{[14– 18]} etc. Among them the shortest pulse duration achieved by these means is about 78 as^[11] and sub-10 as^[12] from the experimental and the theoretical sides, respectively. However, most of the above harmonics and attosecond pulses^{[9– 18]} are generated from the single-electron-approximation (SEA) model.

Recently, Koval et al.^[19] and Feng et al.^[20] respectively investigated the two-electron harmonic emission process. It is found that due to the two-electron sequential and nonsequential double recombination, there is a new harmonic plateau on the two-electron harmonic spectrum beyond the classical single-electron harmonic. As we know that the broader harmonic plateau we get, the shorter attosecond pulse will be obtained. Therefore, we see that the two-electron harmonic extension scheme is a promising way to generate the ultrashort extreme ultraviolet (XUV) pulse.

Thus, in this paper, by solving the two-electron time-dependent Schrö dinger equation (TDSE), we further investigate the two-electron harmonic emission and attosecond pulse generation when a two-electron He atom is exposed to the intense laser pulse. The results show that due to the two-electron double recombination, many new harmonic cutoffs beyond the classical SEA model have been found. Further, by using the two-color field combined with this harmonic extension scheme, two bandwidths with 200  eV have been obtained, which will support a series of sub-60 as XUV pulses.

We consider a two-electron model where each electron is allowed to move along the laser polarization direction. Then, the TDSE with the dipole approximation in the length gauge can be written as (atomic units are used throughout this paper unless stated otherwise)

where

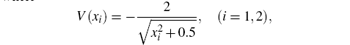
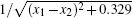
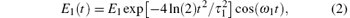
and are the electron– nucleus and the electron– electron interactions, respectively. x₁ and x₂ are the electronic coordinates of the two electrons, which are defined by − 250  a.u. < x₁, x₂ < 250  a.u. with Δ x₁ = Δ x₂ = 0.5  a.u. The absorbing regions on x₁ and x₂ extend over the last 100 grid points. The time space is chosen to be Δ t = 0.1  a.u. The electronic wave function φ (x₁, x₂, t) can be carried out using the standard second-order split-operator method.^{[21– 24]} The laser field can be expressed as

for the single-color field and

for the two-color field. Here, E_i, ω _i, and τ _i, (i = 1, 2) are the amplitudes, the frequencies, and the pulse durations (FWHM) of the 5  fs/800  nm and the 10  fs/1600  nm pulses. φ is the relative phase between the two pulses.

According to the Ehrenfest theorem, ^[25] the time-dependent dipole acceleration can be calculated by

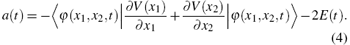
The HHG spectra can be obtained by Fourier transforming the time-dependent dipole acceleration a(t)

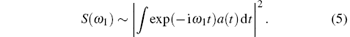
Finally, the attosecond pulse can be obtained by harmonic superposing as follows:

where .

Figure  1 shows the harmonic spectra of the two-electron He model (solid black line) and the SEA He model (dash red line), respectively. The laser field is the single-color 5  fs/800  nm pulse with I₁ = 5.0 × 10¹⁴  W/cm² (I = E²). Clearly, for the SEA model, the harmonic cutoff (E_cutoff = 76ω ₁) is in good agreement with the classical value I_p1 + 3.17U_p, where I_p1 = 24.6  eV is the first ionization potential of the He atom and U_p = I/4ω ² is the ponderomotive energy of the free electron in the laser field. For the two-electron He model, it shows that except for the classical SEA harmonic cutoff, there is a weak extended plateau on the harmonic spectrum.

Fig.  1.

	Figure Option ViewDownloadNew Window
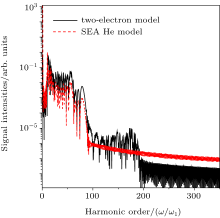	Fig.  1. HHG spectra from the two-electron He atom (solid black line) and the SEA He model (dash red line). The laser field is 5  fs/800  nm, I1 = 5.0 × 1014  W/cm2.

According to the former investigations, ^{[19, 20]} we know that the harmonic extension is caused by the two-electron double recombination. Here, we illuminate it in brief. As we know, the harmonic follows ionization, acceleration and recombination in every half of the laser cycle, and the emitted energies are estimated by E_HC = v²/2, v = − ∫ E(t)dt. For instance, under the present single 5-fs laser pulse, there are three main half cycles, as shown in Fig.  2(a), marked as A– B– C, B– C– D, and C– D– E processes, respectively. Thus, recombination of the single electron will occur three times to produce three different cutoffs E_HC1 = 44ω ₁, E_HC2 = 60ω ₁, and E_HC3 = 38ω ₁, as shown in Fig.  2(b). Now, if a two-electron model is considered, each of the two electrons will occur three times recombination under the present laser pulse. If the two electrons are simultaneously recombined (Fig.  2(c)), then the possible return energies will be I_p1(16ω ₁) + I_p2(35ω ₁) + 2E_HC1 = 139ω ₁, I_p1 + I_p2 + 2 × E_HC2 = 171ω ₁, and I_p1 + I_p2 + 2E_HC3 = 127ω ₁, which is called the sequential double recombination.^[20] Secondly, if the double recombination of the two-electron has a time delay, i.e., the double recombination occurs in a half cycle delay (Fig.  2(d)) or one cycle delay (Fig.  2(e)), then the possible return energies will be I_p1 + I_p2 + E_HC2 + E_HC1 = 155ω ₁, I_p1 + I_p2 + E_HC3 + E_HC2 = 149ω ₁ (for half cycle delay), and I_p1 + I_p2 + E_HC3 + E_HC1 = 133ω ₁ (for one cycle delay), which is called the nonsequential double recombination.^{[19, 20]}

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. (a)  Laser profile of the 5  fs/800  nm, I = 5.0 × 1014  W/cm2 pulse. (b)  The SEA recombination energies under the above laser pulse. Time is in units of optical cycle (o.c.) of an 800-nm pulse in all the following figures unless stated otherwise. (c)– (e) Two-electron double recombination schemes with recombination delay time equaling to zero, half laser cycle, and one laser cycle, respectively. (c)  Ecutoff = Ip1 + Ip2 + 2EHC1, Ip1 + Ip2 + 2EHC2, Ip1 + Ip2 + 2EHC3. (d)  Ecutoff = Ip1 + Ip2 + EHC2 + EHC1, Ip1 + Ip2 + EHC3 + EHC2. (e)  Ecutoff = Ip1 + Ip2 + EHC3 + EHC1.

From the above investigations, we can confirm that the two-electron harmonic spectra can remarkably enhance the harmonic cutoff. Thus, for further extension and optimization of the harmonic spectra, the two-color field scheme has been employed to produce the two-electron harmonic spectra.

Figure  3(a) shows the two-electron (solid black line) and SEA (dash red line) harmonic spectra of the He atom driven by the two-color laser field, consisting of the 5  fs/800  nm pulse with I₁ = 5.0 × 10¹⁴  W/cm² and the 10  fs/1600  nm pulse with I₂ = 1.0 × 10¹⁴  W/cm², φ = 0.0π . Clearly, the harmonic cutoff of the two-color two-electron model is remarkably enhanced in comparison with the single-color field case (see Fig.  1) and the two-color SEA mode. As a result, two supercontinuum bandwidths with 200  eV and 208  eV on the first and the second plateau have been obtained, which will support the generation of the favorable attosecond pulses. Figures  3(b) and 3(c) show the controlling wavelength and pulse intensity effects on the two-electron harmonic emission. The other parameters are the same as those in Fig.  3(a). As we know that the maximum harmonic cutoffs (E_max = I_p + nU_p) are decided by either the amplitude intensities (relating to the pulse intensities) or the widths (relating to the frequencies) of the half-cycle laser profiles.^[26] Thus, with the increasing of the controlling wavelength and the enhancing of the controlling pulse intensity, the harmonic cutoffs have been further extended due to the instantaneous reduction of the central frequency as well as the enhancement of the amplitude of the laser field. However, the large modulations on the harmonic plateaus are unbeneficial to the attosecond pulse generation. Thus, through our calculations, λ ₂ = 1600  nm combined with I₂ = 1.0 × 10¹⁴  W/cm² are the suitable controlling wavelength and intensity for harmonic extension. Figure  3(d) shows the relative phase effect on the harmonic spectra. Clearly, the maximum cutoff energy is achieved when the relative phase φ = 0.0π . Increasing of the relative phase φ , only leads to harmonic cutoffs move towards the low harmonic orders.

Fig.  3.

Figure Option ViewDownloadNew Window

Fig.  3. (a) Two-electron (solid black line) and SEA (dash red line) harmonic emission spectra of He atom driven by the two-color field, consisting of the 5  fs/800  nm, I1 = 5.0 × 1014  W/cm2 pulse and the 10  fs/1600  nm, I2 = 1.0 × 1014  W/cm2, φ = 0.0π pulse. (b)– (d) Controlling wavelength, controlling pulse intensity, and relative phase effects on the two-electron harmonic spectra, respectively.

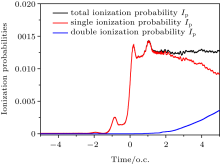
Figure  4 shows the ionization probabilities of the total ionization, single ionization and the double ionization for the present laser pulse. We see that the single ionization is almost dominated by the ionization process at the beginning of the laser. However, after about 1.0 o.c. (o.c. means the optical cycle of the 800-nm pulse), the double ionization begins to enhance, while the single ionization is decreased but still larger than the double ionization at the end of the laser, which is responsible for different yields between the SEA plateau and the extended new plateau on the harmonic spectra.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The single, the double, and the total ionization probabilities for the present laser pulse.

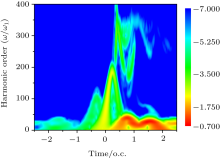
To better understand the two-electron harmonic emission characteristic in Fig.  5, we present the optimal two-color two-electron time-frequency harmonic distribution (Fig.  3(a) solid black line), obtained by using the wavelet transformation of the dipole acceleration a(t)^{[27, 28]}

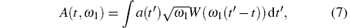
where W(ω ₁(t′ − t)) is the Morlet wavelet, which can be expressed as

Here, α = 30 in our calculations. Clearly, the harmonic energies exhibit two parts. One is the SEA region under the 197ω ₁ harmonic order, which agrees well with the first plateau on the two-electron spectrum shown in Fig.  3(a). Moreover, each energy receives two similar contributions, named the short and the long quantum paths, ^[29] which are responsible for the interference on the harmonic spectrum. While, the other one is the extended weak energies higher than 197ω ₁, which is caused by the second electron recombination. As we know that the higher harmonic cutoff we get, the higher photon energy of the generated pulse will be obtained. Thus, we see that the extended harmonic plateau caused by the two-electron harmonic emission scheme is much better for the generation of the attosecond pulse with higher photon energy.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Time-frequency distribution of the optimal two-color two-electron harmonic spectrum.

Figure  6 shows the temporal profiles of the generated attosecond pulses from the optimal two-color two-electron harmonic emission spectrum (Fig.  3(a) solid black line). Particularly, on the first plateau, by properly superposing the harmonics from the 70th to the 110th order or from the 110th to the 150th order, two isolated XUV attosecond pulses with durations of 55  as and 56  as have been obtained as shown in Fig.  6(a). On the second plateau, by properly superposing the harmonics from the 215th to the 255th order, a 52  as XUV pulse train can be obtained as shown in Fig.  6(b). However, due to the fact that the secondary highest attosecond pulse is too weak, this generated attosecond train can be viewed as an isolated attosecond pulse. But if we further superpose the higher harmonics, the secondary highest attosecond pulse will be enhanced, which is unbeneficial to generate the isolated attosecond pulse, as shown in Fig.  6(c) for the example case of superposing the harmonics from the 255th to the 295th order.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Temporal profiles of the XUV pulses by superposing the harmonics (a) from the 70th to the 110th order or from the 110th to the 150th order, (b) from the 215th to the 255th order, and (c) from the 255th to the 295th order.

In conclusion, we theoretically investigate the two-electron harmonic emission and the attosecond pulse generation when the He atom is exposed to the intense laser pulse. The results show an extended harmonic plateau caused by the two-electron double recombination scheme. Further, by using and optimizing the two-color field combined with this two-electron harmonic extension scheme, a series of isolated sub-60as XUV pulses can be obtained.