Cite this Article
Xiao Rui-Chun, Wu Hai-Xin, Ni You-Bao, Wang Zhen-You, Huang Chang-Bao, Cheng Xu-Dong. First-principles study on linear and nonlinear optical properties of ZnGeP2* . Chinese Physics B, 2015, 24(3): 034205  
Permissions
First-principles study on linear and nonlinear optical properties of ZnGeP2*
Xiao Rui-Chuna),b), Wu Hai-Xina)†, Ni You-Baoa), Wang Zhen-Youa), Huang Chang-Baoa),b), Cheng Xu-Donga),b)
Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
University of Chinese Academy of Sciences, Beijing 100049, China

†Corresponding author. E-mail: hxwu@ircrystal.com

*Project supported by the National Natural Science Foundation of China (Grant No. 51202250) and the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant No. 13J131211).

Abstract

The study of the linear and nonlinear optical properties of ZnGeP2 based on density functional theory has been carried out. In order to get a more physical picture in the infrared region, terms which are considered as the phonon effect were added to the calculated refractive dispersion curves. The phonon-corrected calculation curves show excellent agreement with experimental refractive indexes, which gives a better comprehension of the linear optical proprieties in the transparent region. The static nonlinear optical susceptibility was investigated using approaches based on the “sum over states” and the 2 n + 1 theorem methods. Both of the results of these two methods reasonably coincided with the experimental results.

Keyword: 78.20.–e; 42.65.–k; ZnGeP2; phonon effect; 2 n + 1 theorem; “sum over state” method
1. Introduction

Ternary chalcopyrite 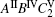(A = Zn, Cd; B = Ge, Si; C = P, As) crystals are promising for optical conversion applications in solid state laser systems. Among these, zinc germanium phosphide (ZnGeP2) is an excellent infrared (IR) nonlinear optical (NLO) crystal, which not only has the common merits of chalcopyrite structure crystals but also exhibits very good thermal and mechanical properties. Owning to these advantages, ZnGeP2 is widely used for frequency conversion in the mid-IR region.[1, 2]

Normally, the transmission window of ZnGeP2 is bounded by the band edge at 620  nm and by an intense two-phonon absorption peak at 13  μ m, [3, 4] the phonon effect related to dispersion should be considered in this region. Density functional theory (DFT) is a widely used method in NLO crystal theoretical studies. Most of previous DFT studies[5– 10] on linear optical property calculation for NLO crystals were simply based on the electronic response to the light. This method gave a relative reliable birefringence result. However, the phonon effect was ignored in the calculation, which caused obvious discrepancies between the experimental and the calculated refractive dispersion curves; that is to say, the calculated curves were nearly flat in the mid/far-IR regions while the experiment curves were downward.

In fact, there are hardly any reports on the influence of the phonon effect, except for the CdSiP2 and CdSiAs2[11] crystals first-principles optical calculation. In this paper, the calculated refractive dispersion curves of ZnGeP2 crystal were corrected with the phonon effect considered. The agreement between phonon-corrected calculation curves and the experiment data is very good, which gives a reasonable description of the linear optical property for ZnGeP2.

Moreover, static nonlinear optical susceptibility is also important to nonlinear crystals, and extensive attention is attracted to obtain the coefficients from the calculation aspect. With the progress of theory, DFT calculation can now be used to calculate and predict nonlinear optical properties directly. There are two common methods which are used in the framework of DFT to calculate static nonlinear optical susceptibility: traditional “ sum over states” [12, 13] and the recently implemented 2n + 1[14, 15] theorem. In this work, both of these approaches are used intentionally to calculate the static nonlinear optical susceptibility of ZnGeP2 to give more reliable calculated results.

This paper is organized as follows. In Section  2, we describe briefly the details of our computational approach. The calculated results are listed in Section  3. A summary of this work is given in Section  4.

2. Computational method

In a crystal, the polarization P can be expressed as a Taylor expansion of the macroscopic electric field, E, according to

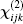
where and are linear and nonlinear optical susceptibilities, respectively.

Usually, in the framework of random-phase approximation (RPA), the expression of the linear optical susceptibility χ (1) is

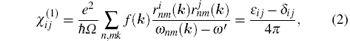
where ε ij is the ij component of the dielectric tensor and rnm is the position matrix element.

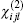
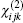
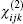
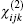
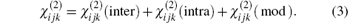
The “ sum over state” method considers that the nonlinear optical susceptibility can be divided into three major contributions: the inter-band transitions (inter), the intra-band transitions (intra), and the modulation of inter-band terms by intra-band terms (mod)

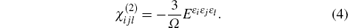
Anther method to calculate the nonlinear optical susceptibility , as described above, is the 2n + 1 theorem. In this scheme the computation of energy derivatives up to third order only requires the ground-state and first-order wavefunctions, the nonlinear optical susceptibility is calculated by a third-order derivative of the energy with respect to low-frequency electric field, that is

Earlier studies indicated that the electronic band of ZnGeP2 crystal could be derived from the indirect gap in GaP, and the experiment indicated a direct band gap.[16, 17] The calculated band gaps were indirect when local density approximation (LDA) exchange-correction energy was used, [16, 18] while the result was direct when generalized gradient approximation (GGA) was employed.[17] Therefore, GGA (PBE[19]) is applied to calculate the linear and nonlinear optical susceptibilities in “ sum over states” method.

Our calculation is based on density functional theory (DFT) and pseudo-potential plane wave method implemented in ABINIT[20, 21] package. LDA[22] is used to calculate the static nonlinear optical susceptibility in 2n + 1 theorem calculation. Troullier– Martins[23] norm-conserving pseudo-potentials are used in both two methods. All of our calculations involve an eight-atom tetragonal primitive cell. The original lattice constants and internal coordinate used in our calculation are taken from the experimental values.[24] For Zn 3d104s2 electron, for Ge 4s24p2, and for P 3s23p3 electrons are treated as valence electrons. A high plane-wave energy cutoff of 40 Hartree and 4 × 4 × 4 Monkhorst– Pack k-points mesh are found to be sufficient to reach convergence for the lattice relaxation and the band structure calculation. In the “ sum over state” optical property calculation, the k-points mesh increases to 10 × 10 × 10, and the valence bands increase to 70.

The calculated band gap by GGA is 1.06  eV, while the experimental data are 2.0 or 2.1  eV; [25] GGA is well known to underestimate the band-gap by up to 100%. Therefore, a scissors operator is usually introduced to shift all of the conduction bands to agree with the measured value of the band gap.

3. Results
3.1. Refractive indexes and birefringence

For chalcopyrite structure with space group of 42m, the dielectric tensor is

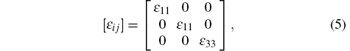
i.e., there are two independent tensor elements. Below the gap, the imagined parts of the tensor compounds trend to zero, and can be ignored. Normally, the relationship between dielectric tensor and the refractive index are

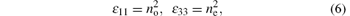
where no and ne are two principal refractive indexes which are parallel and perpendicular to the optical axis respectively.

The calculated refractive dispersion curves in the transparent region are shown in Fig.  1(a). First, the refractive indexes are overestimated compared with the experimental data. This may be mainly caused by the lack of local field effect in the calculations.[26] Second, and more importantly, the origin of dispersion properties for semiconductors in the transparent regions is mainly attributed to two basic physical processes: the electronic transition and phonon effect, and these processes to dispersion properties can be exactly described by the Sellmeier[27– 29] equation. Normally, the Sellmeier equation containing two poles terms, which is

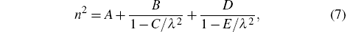
is sufficient for most IR NLO crystals, where the second term can be interpreted as electronic band gap absorption and the last term is related to phonon effect.[11, 30, 31] However, previously and in our calculation, only the electronic response to the light is considered. Therefore, the calculated curves are fitted using formula (7) initially without the last term, the coefficients A, B, and C are extracted. Since the phonon effect is not included in our first-principles calculation, a term acting as the phonon effect is added to the calculated refractive dispersion curve equation. For both the ordinary and extraordinary refractive dispersion curves, the phonon effect can be considered equal in the two curves, approximately, so the two phonon effect terms are the same here. The E represents the square of the average absorption wavelength in units of μ m for phonon absorption frequency[30, 32] (or transverse optical (TO) phonon frequency), while the D here is like a “ scale factor” of the phonon effect. Here, the selections of parameters D and E are taken from Ref.  [11]: the E parameters take the same values of 660  μ m2, and the D parameters do not vary much between the various chalcopyrite structures and are taken as 1.5. As mentioned above, the refractive indexes are overestimated, so the A parameters are slightly adjusted to correct the overestimate to match the experimental data. Finally, the expressions of phonon-corrected calculation curves are

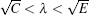
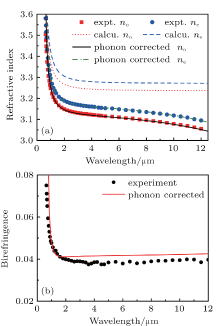where λ is given in micrometers. The corrected calculated curves are shown in Fig.  1(a), the maximal relative deviations of calculated results with experiment data were less than 2% in the whole transparent region and less than 0.1% after 1  μ m. Generally, the transparent regions are , hence the phonon effect term is negative, and makes the refractive dispersion curve downwards. The phonon-corrected calculation birefringence (ne– no) curve is shown in Fig.  1(b). It is found that the agreement of phonon-corrected birefringence with the experimental values is better than 10%. Besides, calculated birefringence curve without phonon effect correction is nearly flat after 3  μ m; the phonon-corrected calculation birefringence curve increases with the increasing of the wavelength, so do the experimental birefringence. This method may be suitable for other IR crystals with the determination of phonon effect term parameters D and E.

Fig.  1. (a) Calculated, phonon-corrected and experimental refractive dispersion curves of ZnGeP2, (b) phonon-corrected calculation birefringence curve of ZnGeP2. Experimental data are taken from Ref.  [25].

3.2. Static nonlinear optical susceptibility

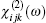
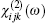
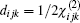
Now, we focus on the results for the nonlinear optical susceptibility in the zero-frequency limit. The second-order nonlinear optical susceptibility is a third-rank tensor. In the literature about nonlinear optics, instead of using this tensor, was used preferably, which can be contracted to a 3 × 6 matrix dil using the following simplified indices:

For ZnGeP2, the dil tensor has only one independent element. The form of this tensor is given by

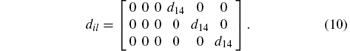
The calculated results obtained by these two methods are listed in Table  1, both of which coincide with the experimental results reasonably. The “ sum over state” result in our calculation is closer to the experimental data than that in Ref.  [16]. In all probability, this mainly happens because a linear muffin-tin orbitals method, which is efficient but less precise, was adopted in Ref.  [16], while the more precision pseudo-potential plane wave method is adopted in this paper.

Table 1. The measured and calculated static nonlinear optical susceptibilities (in units of pm/V) of ZnGeP2.

In general, polarization depends on electrons as well as phonons. The second-order nonlinear optical polarization belongs to higher-order polarization, the phonon effect should affect the SHG coefficients. In the present paper, we deal only with the electronic contribution of the two methods. Compared with the previous results, [16, 35, 36] the calculated SHG coefficients matched to the experiments reasonably, even though only the electronic effect was considered, which indicated less contribution from the phonon effect.

4. Conclusion

The phonon-corrected refractive dispersion curves give a reasonable description of the linear optical property of ZnGeP2, which indicates the importance of phonon effect in the transparent region for IR NLO crystals. Phonon effect coefficients D and E are taken from experimental and empirical values, so the method to obtain two coefficients directly from the calculation approach must be improved in the future. The static nonlinear optical susceptibility calculated by the two methods is in reasonable agreement with experimental results, the 2n + 1 theorem provides a new method to predict static nonlinear optical susceptibility for a NLO crystal.

Acknowledgments

We thank the Center for Computational Science, CASHIPS, China for providing computer platform support. We acknowledge our useful discussions with Associate Professor Lu Wen-Jian and Dr. Shao Ding-Fu in the Institute of Solid State Physics, China.

Reference
1 Ohmer M C and Pand ey R 1998 MRS Bull. 23 16 DOI:10.1557/S0883769400029031 [Cited within:1] [JCR: 5.024]
2 Yao B Q, Li G, Zhu G L, Meng P B, Ju Y L and Wang Y Z 2012 Chin. Phys. B 21 34213 DOI:10.1088/1674-1056/21/3/034213 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
3 Schunemann P G and Pollak T M 1998 MRS Bull. 23 23 DOI:10.1557/S0883769400029043 [Cited within:1] [JCR: 5.024]
4 Isomura S and Masumoto K 1971 Physica Status Solidi (a) 6K139 DOI:10.1002/(ISSN)1521-396X [Cited within:1]
5 Bai L, Lin Z S, Wang Z, Chen C and Lee M H 2004 J. Chem. Phys. 120 8772 DOI:10.1063/1.1687338 [Cited within:1] [JCR: 1.578]
6 Bai L, Lin Z S, Wang Z Z and Chen C T 2008 J. Appl. Phys. 103 083111 DOI:10.1063/1.2907709 [Cited within:1] [JCR: 0.71]
7 Lin J, Lee M H, Liu Z P, Chen C T and Pickard C J 1999 Phys. Rev. B 60 13380 DOI:10.1103/PhysRevB.60.13380 [Cited within:1]
8 Lin Z S, Lin J, Wang Z Z, Chen C T and Lee M H 2000 Phys. Rev. B 62 1757 DOI:10.1103/PhysRevB.62.1757 [Cited within:1]
9 Lin Z S, Wang Z Z, Chen C and Lee M H 2001 J. Appl. Phys. 90 5585 DOI:10.1063/1.1413711 [Cited within:1] [JCR: 0.71]
10 Lin Z S, W Z Z, Chen C T and Lee M H 2001 Acta Phys. Sin. 50 1145(in Chinese) http://118.145.16.217/magsci/article/article?id=17382760 [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
11 Lambrecht W R and Jiang X 2004 Phys. Rev. B 70 045204 DOI:10.1103/PhysRevB.70.045204 [Cited within:3]
12 Rashkeev S N, Lambrecht W R L and Segall B 1998 Phys. Rev. B 57 3905 DOI:10.1103/PhysRevB.57.3905 [Cited within:1]
13 Sharma S and Ambrosch-Draxl C 2004 Phys. Scr. T109 128 DOI:10.1238/Physica.Topical.109a00128 [Cited within:1]
14 DalCorso A, Mauri F and Rubio A 1996 Phys. Rev. B 53 15638 DOI:10.1103/PhysRevB.53.15638 [Cited within:1]
15 Veithen M, Gonze X and Ghosez P 2005 Phys. Rev. B 71 125107 DOI:10.1103/PhysRevB.71.125107 [Cited within:1]
16 Rashkeev S N, Limpijumnong S and Lambrecht W R 1999 Phys. Rev. B 59 2737 DOI:10.1103/PhysRevB.59.2737 [Cited within:5]
17 Shaposhnikov V L, Krivosheeva A V, Borisenko V E, Lazzari J L and d'Avitaya F A 2012 Phys. Rev. B 85 205201 DOI:10.1103/PhysRevB.85.205201 [Cited within:2]
18 Limpijumnong S, Lambrecht W R and Segall B 1999 Phys. Rev. B 60 8087 DOI:10.1103/PhysRevB.60.8087 [Cited within:1]
19 Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 DOI:10.1103/PhysRevLett.77.3865 [Cited within:1] [JCR: 7.943]
20 Gonze X, Rignanese G M and Verstraete M et al. 2005 Z. Kristallogr. 220 558 DOI:10.1524/zkri.220.5.558.65066 [Cited within:1] [JCR: 1.241]
21 Gonze X, Amadon B and Anglade P M et al. 2009 Comput. Phys. Commun. 180 2582 DOI:10.1016/j.cpc.2009.07.007 [Cited within:1] [JCR: 3.078]
22 Perdew J P and Wang Y 1992 Phys. Rev. B 45 13244 DOI:10.1103/PhysRevB.45.13244 [Cited within:1]
23 Troullier N and Martins J L 1991 Phys. Rev. B 43 1993 DOI:10.1103/PhysRevB.43.1993 [Cited within:1]
24 Verozubova G, Gribenyukov A and Mironov Y P 2007 Inorg. Mater. 43 1040 DOI:10.1134/S0020168507100020 [Cited within:1] [JCR: 0.376]
25 Nikogosyan D 2006 Nonlinear Optical Crystals: A Complete Survey 96 106 [Cited within:1]
26 Gajdoš M, Hummer K, Kresse G, Furthmüller J and Bechstedt F 2006 Phys. Rev. B 73 045112 DOI:10.1103/PhysRevB.73.045112 [Cited within:1]
27 Klingshirn C 2007 Semiconductor Optics(3th edn. ) Berlin Springer 73 90 [Cited within:1]
28 Bass M, DeCusatis C, Enoch J, Lakshminarayanan V, Li G, Macdonald C, Mahajan V and Van Stryland E 2009 Hand book of Optics (Vol. II) (2nd edn. ) New York McGraw-Hill, Inc. 33. 01 33. 101 [Cited within:1]
29 Klocek P 1991 Hand book of Infrared Optical Materials Texas CRC Press 54 57 [Cited within:1]
30 Ghosh G 1997 Appl. Opt. 36 1540 DOI:10.1364/AO.36.001540 [Cited within:2] [JCR: 1.689]
31 Tatian B 1984 Appl. Opt. 23 4477 DOI:10.1364/AO.23.004477 [Cited within:1] [JCR: 1.689]
32 Bhar G C and Ghosh G 1979 J. Opt. Soc. Am. 69 730 DOI:10.1364/JOSA.69.000730 [Cited within:1] [JCR: 2.21]
33 Levine B 1973 Phys. Rev. B 7 2600 DOI:10.1103/PhysRevB.7.2600 [Cited within:1]
34 Kumar V, Tripathy S K, Jha V and Singh B P 2014 Phys. Lett. A 378 519 DOI:10.1016/j.physleta.2013.11.049 [Cited within:1] [JCR: 1.11]
35 Hughes J L P and Sipe J E 1996 Phys. Rev. B 53 10751 DOI:10.1103/PhysRevB.53.10751 [Cited within:1]
36 Rashkeev S N and Lambrecht W R L 2001 Phys. Rev. B 63 165212 DOI:10.1103/PhysRevB.63.165212 [Cited within:1]