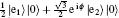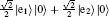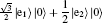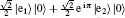The polarization of light and photons stands as one of the corner stones and is one of the most popular names in optics and photonics. As an intrinsic ingredient of electromagnetic waves, lights and photons, the polarization has played a pivotal role in many optical phenomena involving light– matter interaction, including optical birefringence, Fresnel reflection, Brewster angle, ^[1] Mie scattering, ^[2] photonic band gaps, ^{[3, 4]} surface plasmon polaritons^{[5, 6]} in the classical physics world, Bell states, quantum entanglement and interferometer, ^{[7, 8]} quantum information and computing^[9] in the quantum physics world, etc.

In essence, the polarization of light can be arbitrary based on the superposition of two basic orthogonal polarization states, say, the vertical and horizontal linear polarization. Variance of the relative phase and amplitude between these two basic polarization states leads to linear polarization at arbitrary angles, left and right circular polarizations, left and right elliptical polarizations, and many other possibilities.^{[1, 2]} These different polarization states can be used to manipulate the properties of optical information transport and light– matter interaction. Similar concepts are also familiar with other types of classical waves, such as sonic waves, phononic waves, elastic waves, and seismic waves. A question naturally arises: Can the concept of “ polarization” be extended to describe quantum particles and objects, such as atoms that are described by quantum states? In this work we will show that the concept is very useful in describing and manipulating the interaction of a V-type three-level atom (with two upper states close in energy level) with photons confined within a single-mode optical cavity.

Recently, considerable interest has been given to the research of three-level atoms interacting with electromagnetic field. When two of the three levels are very close to each other in energy, significant quantum interference can occur between these two levels. Various interesting results have been demonstrated, such as optical instabilities, ^[10] laser without inversion and inversion without lasing, ^[11] electromagnetically induced transparency, ^{[12– 14]} and large Kerr nonlinearities.^[15] In addition to these topics, spontaneous emission has  attracted increasing attention due to its potential insight into many fundamental physical effects. In particular, many interesting novel properties have been discovered for atoms embedded within optical micro/nano-structures.^{[16– 23]} It was shown that if a three-level atom is embedded in a photonic band gap structure, quantum interference is greatly weakened at the band gap edge, ^[16] while the quantum interference effect can be enhanced when considering the isotropic dispersion of Bloch photons in photonic crystals.^[17] For a three-level Λ -type atom embedded in a damped optical cavity, the detuning and the coupling intensity may affect the shape of the spontaneous emission spectrum strongly, ^{[18, 24]} while for a V-type three-level atom in a Fabry– Perot cavity containing left-handed materials, the spontaneous emission spectra can either be narrowed or broadened.^[19] In other cases, the occurrence of inhibition or cancellation of spontaneous emission can arise in a certain condition.^{[20, 21]}

It is now clear that spontaneous emission may be influenced by many factors and exhibits various properties in different conditions. For a three-level V-type atom embedded in a single-mode damped cavity, the spontaneous emission under different initial “ polarized” states of atom has not been explored systematically up to now. Therefore, we will study the spontaneous emission characteristics of such a system when different initial “ polarized” states of atom are prepared. According to the property of Hilbert space, any state in quantum mechanics can be described as a vector of Hilbert space. In the same Hilbert space, the inner product of every two state vectors is orthogonal. Thus, various “ polarized” initial states may be prepared if we imitate the definition of polarized light. We assume that the system is in the superposition state initially. For the state vector | ψ 〉 = a₁ | ψ ₁〉 + a₂ | ψ ₂〉 , where a₁ and a₂ are both real numbers, we can call it “ linearly polarized” state. The state | ψ 〉 = a₁ | ψ ₁〉 + a₂e^iϕ | ψ ₂〉 can be called “ elliptically polarized” state, which includes “ left rotation” and “ right rotation” for different angle ϕ . 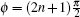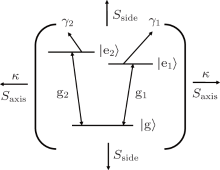In the case of a₁ = a₂ and , the above state is called “ circularly polarized” state. In the following we will find that these “ polarized” states of atoms have a drastic influence on the spontaneous emission spectra of a V-type three-level atom that is strongly coupled with a single-mode damped cavity field in thermal equilibrium.

The system considered is illustrated in Fig.  1. It consists of a three-level V-type atom and a single-mode damped cavity. The two upper levels | e₁〉 and | e₂〉 are coupled to the lower level | g〉 by the coupling constant g_i. The direct transition | e₂〉 → | e₁〉 is forbidden. The resonant frequency of the cavity mode is ω _c. For convenience, we assume that the system temperature is at 0  K, where the dephasing rate of quantum states can be neglected.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematics of a three-level V-type atom embedded in a single-mode damped cavity. Photons can decay from the sides of the cavity and through the axis direction via spontaneous emission modulated by the strong atom– cavity coupling.

Under the rotating wave approximation, the Hamiltonian in the interaction picture without damped term is

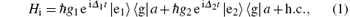
where a⁺ (a) is the creation (annihilation) operator of the cavity mode, | g〉 and | e_i〉 (i = 1, 2) are the ground and excited states of the atom, Δ ₁ = ω _1g − ω _c and Δ ₂ = ω _2g − ω _c are the detuning between the transition frequency of the two upper levels and the resonant frequency of the cavity mode. Considering the spontaneous emission of atom and the dissipation of cavity field, the dissipative Hamiltonian is

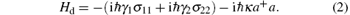
Here σ _ii = | e_i〉 〈 e_i| − | g〉 〈 g| (i = 1, 2). The cavity field is damped at the rate κ , γ ₁ and γ ₂ are the decay rate of spontaneous emission from the two upper levels to the lower level. The Hamiltonian for the system is

The solution and discussion of the Hamiltonian are restricted to the subspace containing zero and one excitations. Thus, the state vector of the system at time t is

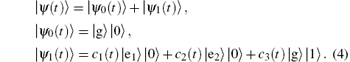
Here | 0〉 and | 1〉 are the vacuum and one-photon state of the cavity field. The zero-excitation component | ψ ₀(t)〉 is invariant under the action of Hamiltonian, so we only consider the dynamics of the single-excitation component | ψ ₁(t)〉 . 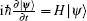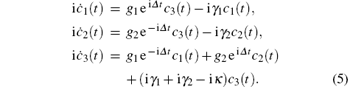For a special case, Δ ₁ = ω _1g − ω _c = − (ω _2g − ω _c) = − Δ ₂ = Δ , the motion for the probability amplitudes c₁(t), c₂(t), and c₃(t) can be derived from the Schrö dinger equation as follows:

To solve the above equation set, we assume a trial solution as c₁(t) = Ae^{i(x + Δ )t}c₂ (t) = Be^{i(x − Δ )t}, and c₃ (t) = Ce^ixt. Inserting the trial solution into Eq.  (5), we can obtain the following equations:

The above equations can be transformed into a set of linear equations of a simple 3 × 3 eigensystem,

Here x is the eigenvalue. By solving the linear equations, we can derive three roots, which are resonance frequency of three harmonic oscillators. The quantum state of the system is the superposition of these harmonic states. Thus, quantum interference arises in this system and is involved in the resonance frequency and probability amplitude of these harmonic oscillators. The general solution of temporal dynamics of the strongly coupled system can be described by these wave functions.

Substitute three eigenvalues into Eq.  (6) and we can obtain

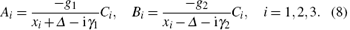
The probability amplitude of three one-excitation states can be obtained by substituting Eq.  (8) into the trial solution,

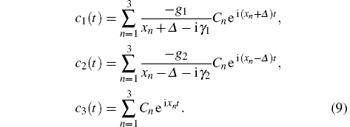
Equation  (9) is achieved in the interaction picture where the Hamiltonian does not contain the H₀ term. These results ought to be transformed in the following way to the quantum states in the Schrö dinger picture:

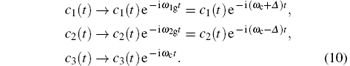
According to the quantum regression theorem, ^[25] it can be found from Eq.  (9) that the spontaneous emission spectrum of this system contains two parts when the time t → ∞ . One is the spectrum from the sides of the cavity, which is determined from the autocorrelation of the atomic dipole amplitude and reads

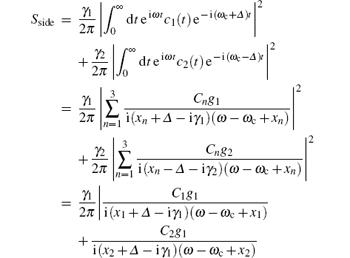
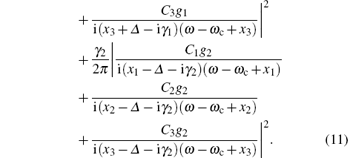
The other is the spectrum along the cavity axis, which is related to the autocorrelation of the cavity field and is given by

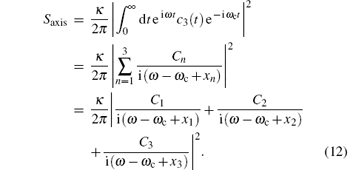
The side spectrum contains two terms caused by the atom, which are c₁(t) and c₂(t), while the axis spectrum only revolves the cavity mode term c₃(t). It can be seen from Eqs.  (11) and (12) that the features of side and axis spectrum rely on the physical parameters g_i, Δ _i, γ _i, κ , and the coefficients C_n. How these physical parameters influence the spectrum has been studied in several papers.^{[18, 26, 27]} In our current study, all these parameters are fixed constants. From Eq.  (9) we can find that the coefficients C_n are determined by initial conditions. Consequently, we can expect that the side and axis spectrum may exhibit different characteristics under different initial conditions corresponding to different “ polarized” states of atom.

We assume that the atom is initially prepared in the superposition state of the two upper levels and the cavity is in vacuum state. The initial state can be described as

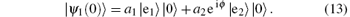
Here a₁ and a₂ are the amplitude of state | e₁〉 | 0〉 and | e₂〉 | 0〉 , respectively, and they are both real numbers, and ϕ is the phase difference of the two states. The initial coefficients of three one-excitation states at time t = 0 are c₁(0) = a₁, c₂(0) = a₂e^iϕ , and c₃(0) = 0. Then equation  (9) can be written as

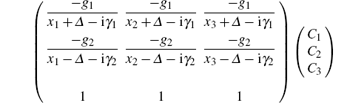
By solving the above equations, we can obtain

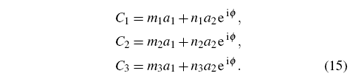
Here, m₁, n₁, m₂, n₂, m₃, and n₃ are all constants related with the physical parameters (g_i, Δ _i, γ _i, κ ) and the harmonic frequency (x_i). Consequently, we can find from Eqs.  (11), (12), and (15) that the characteristics of the side and axis spectrum will be affected by a₁, a₂, and ϕ .

In wave optics, elliptical polarized light can be described as^{[1, 2]}

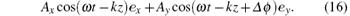
When A_x, A_y, and Δ ϕ , which are all real numbers, take different sets of values, a variety of polarized light states can be obtained based on the superposition of two basic polarization states of optical field, and the horizontal state represented by the unit vector e_x and the vertical state represented by the unit vector e_y. Following this idea, diverse “ polarized” initial states of atom can be prepared by changing the values of a₁, a₂, and ϕ . The side and axis spectrum will be discussed in the following under three categories of “ polarized” states of atom.

In our calculation, we set g₁ = g₂ = 1, Δ ₁ = − Δ ₂ = Δ = − 0.1, and γ ₁ = γ ₂ = κ = 0.01. Obviously, the atom– cavity system is located in the strongly coupled regime. Substituting these values into Eq.  (7), we can get three definite harmonic-frequency eigenvalues (x₁ = 0.01i, x_{2, 3} = ± 1.4177 + 0.01i), which contains both real part and imaginary part. The real part shows the oscillatory behavior of every harmonic wave function, while the imaginary part corresponds to the decay behavior. The three one-excitation states are the superposition of these harmonic wave functions. Therefore, the temporal dynamics of the quantum system may exhibit a complex interference behavior. According to Eqs.  (11) and (12), three peaks are expected at the position of these three eigenvalues in the side and axis spectrum, which correspond to three detuning values: δ = ω − ω _c = − 1.4177, 0, 1.4177.

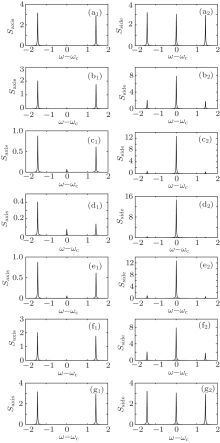
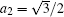
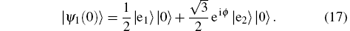
First, we take a look at a general “ elliptical polarized” state of atom. We suppose a₁ = 1/2 and , then the initial state can be written as

This state vector can be called “ elliptical polarized” state. In addition, “ left elliptical polarized” states can be obtained in the condition of 0 < ϕ < π . Likewise, “ right elliptical polarized” states are prepared in the case of π < ϕ < 2π . Using Eqs.  (11) and (12), rigorous numerical results of the spectrum as a function of the detuning δ = ω − ω _c for different “ elliptical polarized” states can be calculated straightforward, and the results are displayed in Fig.  2.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Spontaneous emission spectrum from a three-level V-type atom prepared at various “ elliptical polarized” initial states which can be written as . (a) ϕ = π /4, (b) ϕ = π /2, (c) ϕ = 3π /4, (d) ϕ = π , (e) ϕ = 5π /4, (f) ϕ = 3π /2, and (g) ϕ = 7π /4. Subscript “ 1” represents the spectrum along the cavity axis, while subscript “ 2” represents the spectrum from the sides of the cavity.

Numerical results demonstrate that the axis and side spectrum present three peaks: one center peak is located at the frequency of the cavity mode and two side peaks are located at δ = ± 1.4177. In order to understand the spectrum feature clearly, we neglect the decay terms in Eq.  (7) since the decay parameters are much smaller than the coupling constants (γ _i, κ ≪ g_i). At this end, a simple analytical form of eigenvalues can be acquired as

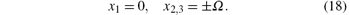
Here Ω is the Rabi oscillation frequency for the three-level V-type atom 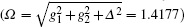. The spontaneous emission will occur accompanied with emission of a photon. For strong coupling, the emitted photon is trapped in the vicinity of the atom by the resonance cavity. The photon may be reabsorbed by the atom because of the strong interaction of the cavity and the atom. Then the photon will be reemitted and reabsorbed a number of times before it leaves the cavity finally. In this process, the oscillatory exchange of energy between the atom and the cavity field leads to a splitting of the emission spectrum into three lines predicted at fixed sites (δ = 0, ± Ω ). Meanwhile, our systematic numerical studies show that the positions of the spectra lines are only dominated by the parameters g_i, Δ , while the imaginary part of eigenvalues corresponding to the decay terms will influence the intensity of the spectrum lines merely.

For both the axis and side spectrum, the intensity of the center peaks first increases and then decreases with the increase of phase difference ϕ . In contrast, the intensity of side peaks first decreases and then increases. That is to say, the variation behavior of the spectrum for “ left elliptical polarized” states is inversed to that for “ right elliptical polarized” states. This periodic phenomenon in spectral variation is caused by quantum interference. The two closely upper levels are coupled to the ground level at the same coupling constants. The interference arising from the two transition channels leads to an exchange of population between the two upper levels.

It is worth noting that in the side spectrum the center spectrum line located at δ = 0 has a high peak as illustrated in Figs.  2(a₂), (b₂), (c₂), 2(d₂), 2(e₂), 2(f₂), and 2(g₂). As described in Eq.  (11), the side spectrum is determined by the autocorrelation of the atomic dipole amplitude, thus the probability amplitude of the two upper quantum states. If the spontaneous transition frequency of the atom is equal to the cavity mode (ω = ω _c), resonance will occur. Thus, drastic spontaneous emission happens. Besides, the intensity of the peak located at δ = 1.4177 is always lower than that of the one located at δ = − 1.4177 since the two basic states have different probability amplitudes (a₁ < a₂). Another remarkable thing is that in the axis spectrum the center line has a much smaller intensity than those of the two side lines. This may also originate from the quantum interference effect, where the spontaneous emission right at the center line (with zero detuning) is contributed from the two down transition channels of the three-level V-type atom. Because they are subject to a phase difference and thus their contributions are largely cancelled due to the destructive interference, leading to a very weak center line intensity.

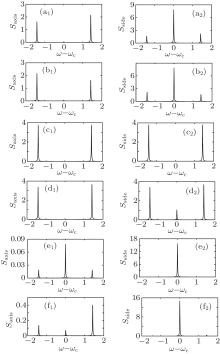
Now we turn to the “ linear polarized” state of atom, which corresponds to ϕ = 0 or π in Eq.  (13). According to wave optics, the linear polarization state is controlled by the relative intensity of two basic unit polarization states, leading to different polarization angles (i.e., oscillation directions of electric field for photons) in real space. Similar operation can be performed to create “ linear polarized” state of a three-level V-type atom at arbitrary polarization angles. Six kinds of “ linear polarized” states (i.e., six different polarization angles) are selected for demonstration in our calculations, and the corresponding results of the axis and side spontaneous emission spectra are displayed in Fig.  3, which clearly show diverse spectral characteristics for different “ linear polarized” states.

It can be seen from Fig.  3 that three peaks exist in every figure and the positions of the peaks are the same as Fig.  2 since all the physical parameters are the same. Similar to the situation of “ elliptical polarized” state, when the polarization angle changes, the absolute strength and their relative ratio of the three spectral lines in both the side and axis spectrum can vary drastically and each spectral line is tunable in a very broad range of intensity. This feature once again clearly demonstrates the power of quantum interference effect in a strongly coupled light– atom interaction system. In Figs.  3(a), 3(d), and 3(f), the peak located at δ = 1.4177 has a higher strength than the one located at δ = − 1.4177 because a₁ > a₂. Similarly, the right peak has a lower strength than the left one as demonstrated in Fig.  3(b). Nevertheless, the two side peaks have equal intensity as shown in Figs.  3(c) and 3(e) in the case of equal probability amplitudes (a₁ = a₂). For the same reason as mentioned in discussion of “ elliptical polarized” states, every side spectrum generally has a higher center peak as shown in Figs.  3(a₂), 3(b₂), 3(d₂), 3(e₂), and 3(f₂). However, the center peak in Figs.  3(c₁) and 3(c₂) almost disappears, which may originate from the destructive interference induced cancellation (a₁ = a₂, ϕ = 0). An interesting thing to find from Figs.  3(a₂) and 3(b₂) that the side spectrum for the case of | e₁〉 | 0〉 is just the mirror image of that for the case of | e₂〉 | 0〉 , which can be attributed to the symmetric distance of the cavity resonance frequency from that of the two upper levels | e₁〉 | 0〉 and | e₂〉 | 0〉 and symmetric Rabi splitting. Another significant feature to find by comparing Fig.  3 with Fig.  2 is that there exists a very big difference in the spontaneous emission spectrum between linear polarized states and elliptical polarized states, even if the relative probability strength of the two upper states is the same. This clearly indicates the pivotal role of the phase difference between the two upper states in shaping their spontaneous emission spectrum when down transitioning to the lower state, and the critical role of quantum interference effect underlying the phenomena.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Spontaneous emission spectrum from a three-level V-type atom prepared at different “ linear polarized” initial states. (a) | e1〉 | 0〉 , (b) | e2〉 | 0〉 , (c) , (d) , (e) , and (f) . Subscript “ 1” represents the spectrum along the cavity axis, while subscript “ 2” represents the spectrum from the sides of the cavity.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Spontaneous emission spectrum from a three-level V-type atom prepared at (a) left circular polarized initial state with ϕ = π /2, and (b) right circular polarized initial state with ϕ = − π /2. Subscript “ 1” represents the spectrum along the cavity axis, while subscript “ 2” represents the spectrum from the sides of the cavity.

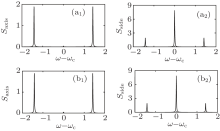
Finally, we examine the situation of “ circular polarized” state, which can be looked upon as a special case of “ elliptical polarized” state. These states can be written as

We can see that the spectrum for “ left circular polarized” state (ϕ = π /2) and “ right circular polarized” state (ϕ = − π /2), as illustrated in Fig.  4, are completely the same. For both the axis and the side spectrum, the side peaks are symmetric because of the equal probability amplitude.

In summary, we have borrowed the concept of photon polarization state and extended it from optics to atomic physics, in particular for a three-level V-type atom with two close-neighboring upper energy levels. The general “ polarization” state of atom is defined as the arbitrary superposition of its two upper levels, characterized by the value of the two probability amplitude (a₁, a₂) and their phase difference (ϕ ). A wide variety of “ polarized” states with linear polarization at arbitrary direction, left and right circular polarization, and left and right elliptical polarization, similar to photons, can be prepared by changing the values of a₁, a₂, and ϕ . Through rigorous numerical calculation and analytical solution, we have found that spontaneous emission of light from these “ polarized” three-level atoms strongly coupled with a damped single-mode optical cavity shows very different profiles of side and axis spectrum, depending on the polarization state. The spontaneous emission spectra exhibit three spectral lines due to Rabi splitting and resonance in the strongly coupled atom– photon system. The absolute intensity of each spectral line and their relative contrast can be finely tuned by changing a₁, a₂, and ϕ , and many interesting spectral features have been found in each category of linear polarization, circular polarization, and elliptical polarization.

Our results indicate that one can control the spontaneous emission of a three-level V-type atom effectively by preparing the atom at an appropriate “ polarized” initial state. Essentially, the strong “ polarization” -dependent spontaneous emission features can be attributed to the quantum interference effect. This indicates that the coherent characteristics of quantum states and their relative contrast in amplitude and phase could provide a powerful means to shape the emission property of atom. In a much broader aspect, the polarization state of atoms can become an active ingredient to manipulate their interaction with light, much the same as polarization of photon used to control light interaction with atoms and other matters. It can be expected that exploitation of the coherent superposition and interference of quantum states and polarization states in atomic system would allow one to deeply explore new frontiers of light– matter interaction. As great progresses have been made in developing technologies to manipulate strong light– atom interaction in free-space^{[28– 30]} and solid-state micro/nano-cavity system, ^{[31– 41]} we believe that these new frontiers of light interaction with “ polarized” atoms can be investigated experimentally, which may lead to new technologies in optical sensing, metrology, quantum computing and communication.