In the strong field, , B₀ ≲ 4.3 × 10⁹  T, which is close to the critical Schwinger field of electron– positron pair production, ^{[1– 4]} the vacuum exhibits properties of nonlinear optical medium, ^{[5– 7]} and leads to photon splitting, ^[8] dichroism, ^[9] birefringence, ^{[10– 14]} and vacuum bragg scattering.^[15] The results of PVLAS collaboration^{[13, 14]} are so close to the polarization rotation in a vacuum with a rotating transverse magnetic field, predicted by Adler, ^[10] Heyl and Hernquist.^[11] Biswas and Melnikov^[12] pointed out that the rotation of a magnetic field does not impact the birefringence. Adler also calculated the refractive indices of the probe wave in a rotation magnetic field and probed the dependence of the refractive indices on the frequency of the magnetic field. However, if there is a strong electric field, E₀, perpendicular to the strong magnetic field, B₀, the propagating characteristics of the wave in the E₀ × B₀ direction and in the − E₀ × B₀ direction are quite different from each other. For E₀ = cB₀, several researchers^{[16– 20]} obtained the refractive index for the “ head-on collision" probe wave (Eqs.  (16) and (17) in Ref.  [19] and Eq.  (15) in Ref.  [20]). Their results also showed that there is no interaction between the probe wave incident in the E₀ × B₀ direction, i.e., the refractive index is unit.

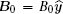
In general, in the field (E, B) of a tightly focused low-frequency laser, | E| < c| B| . If the laser frequency is smaller than 1 × 10²⁰  rad/s, the scaling length of the field is much larger than the Compton wavelength of electron. In that case, the field can be equivalent to the homogenous field and the effective Lagrangian 𝔏 _eff^[5] is available. Therefore, birefringence in a crossed field (E₀ ⊥ B₀ and E₀ ≤ cB₀) should be reconsidered. In order to check birefringence in a more general regime, we consider the interaction between a high-frequency electromagnetic wave and a strong electromagnetic field: , , and E₀ ≤ cB₀, where and are the unit vectors of the x and y directions, respectively.

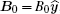
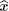
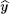
In this paper, we show that the refractive index of a forward wave with the wave vector k ‖ E₀ × B₀ is different from that of a counter propagating wave in a vacuum with a strong homogeneous static electric and magnetic field, solving the Maxwell equations corrected by the effective Lagrangian^[5]

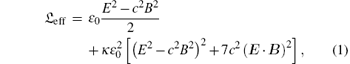
where E and B is the total electric and magnetic field respectively, using

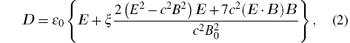
and

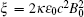
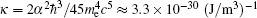
which are valid for | E| , c| B| ≪ E_crit ≈ 10¹⁸  V/m and the frequency of the field ω ≪ ω _e ≈ 10²⁰  rad/s. The quantum parameter, , where ε ₀ is the permittivity of vacuum, , m_e is the electron static mass, and α is the fine-structure constant.

First, the external field is assumed to be and , where and are the unit vectors of the x and y directions respectively, E₀ ≲ cB₀ ≲ 10¹⁸  V/m, which is the critical Schwinger field of electron– positron pair production in a vacuum.

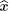
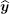
Let E = E₀ + E_q and B = B₀ + B_q be the total electromagnetic field, and E_q and B_q are the nonclassical parts which are expressed as

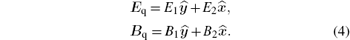
Let | E₁| , | E₂| , | cB₁| , | cB₂| ≪ | E₀| , and | cB₀| , where c is the light velocity. The wave vector . Using the effective Lagrangian 𝔏 _eff, ^[5] the QED corrected electric displacement field D_q = D − ε ₀α ₀E₀ and magnetic field strength are given by

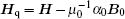
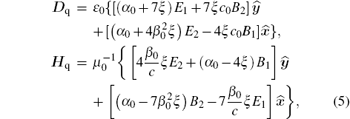
where α ₀ = 1 + 2ξ L̂ ₀, c₀ = E₀/B₀, β ₀ = c₀/c, and 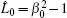. In fact, c₀ is just the drift velocity of the virtual electrons and positrons in the field.

With the wave assumptions that E_{1, 2}, B_{1, 2} ∝ exp[i(kz − ω t)], the linearization of the corrected source-free Maxwell equations

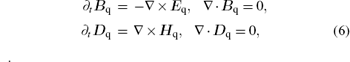
gives

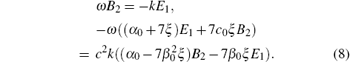
With Eq.  (8), the dispersion relationship for parallel polarization is obtained after some straightforward algebra

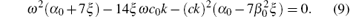
With Eq.  (7), the dispersion relationship for perpendicular polarization is given by

Let n = ck/ω be the refractive index. With Eqs.  (9) and (10), the refractive index of a probe wave propagating in the positive z direction, i.e., in the E₀ × B₀ direction for parallel polarization and perpendicular polarization, is respectively given by

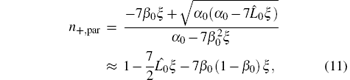
and

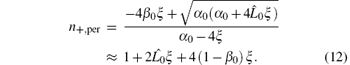
Similarly, the refractive index of a probe wave propagating in the negative z direction, i.e., in the − E₀ × B₀ direction for parallel polarization and perpendicular polarization, is respectively given by

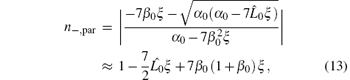
and

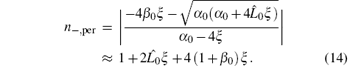
With Eqs.  (11) and (14), the difference of the refractive indices for the parallel polarization and the perpendicular polarization in the E₀ × B₀ direction is obtained as

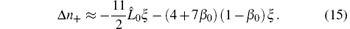
In the − E₀ × B₀ direction, it is obtained as

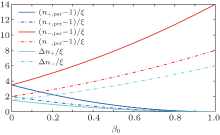
Equation  (15) shows that the difference of the refractive index for the parallel polarization wave and the perpendicular polarization wave is proportional to ξ . Here the wave propagates in the positive z direction, i.e., E₀ × B₀. Equation (16) shows the refractive index for the parallel polarization wave and the perpendicular wave propagating in the negative z direction, i.e., − E₀ × B₀. The results predict the difference of the refractive indices is proportional to ξ . Figure  1 shows the drift effect on vacuum birefringence in a homogenous strong crossed field. The birefringence is amplified by the drift effect for the counter-propagating probe wave and is reduced for the probe wave propagating in the direction of E₀ × B₀.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Drift effect on vacuum birefringence in a homogenous strong crossed field.

To compare our results with that of the literatures, two special cases are considered: (a) E₀ = 0, i.e., vacuum birefringence in the presence of a homogenous magnetic field; (b) E₀ = cB₀ in a crossed field.

For E₀ = 0, c₀ = β ₀ = 0, L̂ ₀ = − 1, and the refractive indices are

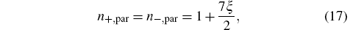
for parallel polarization, and

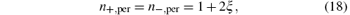
and the difference of the refractive indices is

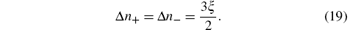
All the results are the same as those of Refs.  [10]– [13]. Therefore, in a homogenous magnetic field, there is no drift velocity of virtual particles and there is no direction dependence of the refraction.

Another well-known case is E₀ = cB₀, β ₀ = 1, and c₀ = c. Therefore, the refractive indices in the E₀ × B₀ direction are trivial and n_{+ , par} = n_{+ , per} = 1. There is no interaction between the probe wave and the crossed field. It is also consistent with Eqs.  (16) and (17) in Ref.  [19] and Eq.  (15) in Ref.  [20] in the E₀ × B₀ direction.

However, for the counter-propagating probe wave, the refractive index is given by

for parallel polarization, and

which is also consistent with Eqs.  (16) and (17) in Ref.  [19] and Eq.  (15) in Ref.  [20] in the − E₀ × B₀ direction.

The refractive indices of the probe wave in the E₀ × B₀ direction and in the − E₀ × B₀ direction are different from each other. The difference of the refractive indices for parallel polarization and perpendicular polarization are also different in the two directions. Define

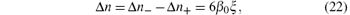
which tends to be zero as E₀ → 0.

The physics of the direction dependence of the refractive index maybe the E₀ × B₀ drift of the virtual electrons and positrons in the strong field. The virtual electrons and positrons have the same E₀ × B₀ drift velocity, . Therefore, it induces the direction dependence of refraction. Equation  (22) shows that the difference is proportional to the drift velocity.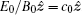

In the experiment to measure the birefringence, the light is reflected and propagates through the field forward and backward repeatedly for N times. Set the longitudinal length of the field as L, the elipticity value^[14] is given by

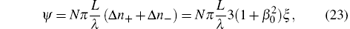
which is times that in a strong magnetic field.

In conclusion, vacuum birefringence is different in the E₀ × B₀ direction and in the − E₀ × B₀ direction. The E₀ × B₀ drift of the virtual electrons and positrons may be the key point. The influence of the drift effect on the ellipticity in the experiments has been given explicitly.