One of the main focal aspects of modern science is the realization of a full-scale quantum computer.^{[1– 7]} It is widely believed that Shor’ s factoring algorithm provides a driving force to boost quantum computing research. In theory, factorizing N by a full-scale Shor's algorithm could be achieved by about 72⌈ log₂N⌉ ³ binary quantum gates.^[8] In practice, the large number of quantum gates places a serious obstacle to the algorithm's implementation. According to the present technologies, small-scale quantum computing devices built on a variety of physical systems exist in the laboratory and have demonstrated the fundamental characteristics for building systems. On the nuclear magnetic resonance system, 15 is factorized.^[9] The same work is also demonstrated on a photonic system^[10] and on a photonic chip.^[11] These are binary demonstrations. Binary quantum computation is built upon the quantum bit (or qubit for short), which is a two-level quantum system that can be represented mathematically by a vector in a two-dimensional Hilbert space.^[12] Realizing qubits usually enforces a two-level structure on systems by convention and not by physical reality, which is naturally far more complex and has many readily accessible degrees of freedom.

Nowadays, higher-dimensional quantum systems with more degrees of freedom have been studied, which can exponentially extend the Hilbert space on the same system.^[13] For example, the Toffoli gate is simplified by involving a third level of the qubits.^[14] Higher-dimensional systems enable the evolution from binary (qubit) to non-binary (qudit) quantum computing.^[15] The main advantage of non-binary computing is the exponential increases of speed and capacity when increasing the encoding elements, ^[16] thus significantly reducing the number of elemental gates required to build key quantum circuits.^{[14, 17, 18]} The scheme introduced in Ref.  [19] is an appropriate model to study non-binary quantum computing because it allows control of the vibrational states of an ion adiabatically using electric fields. A progression of several vibrational states can be employed to execute simple quantum algorithms using a single trapped ion. The state-to-state transitions between vibrational states of the ion are slightly anharmonic, thus occur at slightly different frequencies and can be controlled selectively. In such a scenario, the frequency content of shaped electric fields should be in the MHz range. In recent years, several anharmonic ion traps have been shown to be suitable for practical implementation.^{[20– 24]}

In this paper, we propose optimization schemes for Shor’ s algorithm implementation and take a ternary version for factorizing 21 as an instantiation. It turns out that the specific factorization is achieved by a two-qutrit quantum circuit, which consists of only two single qutrit gates and one ternary controlled-NOT (TCNOT) gate. This is a representative advantage compared to the previous studies.^{[10, 11]} By randomly choosing 4 as the base in our implementation, the period of the modular exponential function is 3, i.e., the order is 3. Traditionally, the orders of the previous studies^{[10, 11]} are even integers. Our implementation technique is independent of the physical encoding of quantum information and the way in which the elemental gates are themselves constructed. Therefore, we encode the two-qutrit quantum circuit into the lower nine vibrational states of the trapped ion.^[19] Optimal control theory (OCT) is employed to derive the manipulation field for transferring the encoded states. The manipulation can be achieved in two ways: separately implement the elementary ternary gates step-by-step or implement the whole algorithm in one step.^[25] Numerical simulation results show that the accuracy of the state transformations is about 0.9919 for the one step implementation.

The remainder of this paper is organized as follows. In Section  2 we discuss optimization process of the ternary Shor’ s algorithm. In Section  3 we briefly review the theoretical model and major properties of one ion trapped in anharmonic potential. Section  4 outlines the control problem and the OCT solution to it. The results of the OCT calculations are presented and analyzed in Section  5. Finally, Section 6 provides our conclusion.

Shor’ s algorithm switches the factoring problem to the problem of finding the period of a function. Quantum parallelism is utilized to obtain a superposition of all of the values of the function in one step. The quantum Fourier transform of the function is then computed, thus all of the amplitude of the function is put into multiples of the reciprocal of the period. The period, or the order which in turn is used to factor the integer N, is obtained through high probability measurement of the state. The order-finding part of the algorithm is the kernel, which has been experimentally demonstrated.^{[9– 11]} However, the orders employed in the previous studies were a power of 2.^{[9– 11]} In this section, we generalize the d-dimensional order-finding procedure and optimize the number of qudits, we then factorize 21 by a ternary version to show that an odd order is also feasible.

Theorem 1 The d-dimensional order-finding procedure uses two registers: an argument register and a function register, which consist of ⌈ 2log_dN⌉ qudits and ⌈ log_dN⌉ qudits, respectively.

Proof The main component of the quantum order-finding is the modular exponentiation computing the function of a^x(mod N), where a is a random number chosen from the set {1< a< N} ∩ gcd(a, N) = 1, and x is the argument of the function taking values between 0 and at least N². So, in order to hold a modulo N integer in the function register, ⌈ log_dN⌉ qudits is needed. In addition, the argument register needs to hold at least N² arguments. Through logarithm conversion with base d, we can get that ⌈ 2log_dN⌉ qudits are necessary.

Example Suppose that ternary Shor’ s algorithm were implemented to factor 21. ⌈ log₃21⌉ = 3 qutrits are in the function register. The argument register consists of 6 qutrits (3⁵ = 243 < 21² = 441 < 3⁶ = 729), as shown in Fig.  1(a). However, 9 qubits and 5 qubits are needed in the two quantum registers for the traditional binary order-finding algorithm.^[26] The first step of the procedure is preparation of the argument register in an equally weighted coherent superposition state. This is usually achieved by Hadamard gates. The d-dimensional Hadamard gate is defined as 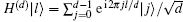. 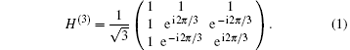The matrix form of the ternary Hadamard gate is

In addition, the following Theorems 2 and 3 show that the number of qudits can be ulteriorly reduced under certain circumstance.

Theorem 2 With pre-determined N and a, if a^dm(mod N) = 1, the necessary n = ⌈ 2log_dN⌉ qudits in argument register can be reduced to m (0 < m < n). Otherwise, such reduction fails.

Proofa^x = a^{dn− 1x_{n− 1}}· · · a^d1x₁a^d0x₀, thus modular exponentiation consists of serial multiplication by a^dk(mod N) for all k, where 0 ≤ k < n. If a^dm(mod N) = 1, thus all a^dk(mod N) = 1 for k ≥ m. In this case, a^x(mod N) simplifies to multiplications controlled by just m qudits.

Example Suppose that a = 4 is randomly chosen. As shown in Fig.  1(a), 4^x(mod 21) can be easily accomplished using 6 consecutive controlled multiplications 4^3ix_i(mod 21), where i = 0, 1, ..., 5. It is clear that 4³(mod 21) = 1, thus, the high-orders, 4^3x₁(mod 21), ..., 4^35x₅(mod 21), are redundant in Fig.  1(a). Such simplification ulteriorly reduces the number of qutrits used in the argument register from 6 to 1. We can then apply the inverse quantum Fourier transform (InvQFT⁽³⁾) to the argument register, followed by a measurement of the population of the qutrit states. One qutrit inverse Fourier transform is also achieved by a ternary Hadamard gate, which is shown in Eq.  (1).

Theorem 3 With pre-determined N and a, if the period of modular exponentiation r is odd, then should be an integer. In addition, if r = d, then the necessary ⌈ log_dN⌉ qudits in function register can be reduced to 1. Otherwise, such reduction fails.

Proof Generally, after r is obtained, it needs to compute gcd(a^r/2 − 1, N) and gcd(a^r/2 + 1, N), and test to see if this is a non-trivial factor. Hence, a^r/2 needs to be an integer, i.e., 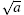is an integer. In addition, r = d means that a^{0, 1, … , d− 1} are different to each other. Then log_a(a^{0, 1, · · · , d− 1}) = 0, 1, … , d − 1, which happens to be the d basis states of a qudit.

Example For a control qutrit, x₀ = 0, 1, 2. i.e., the controlled modular multiplication 4^x₀(mod 21) = 1, 4, 16, and 4³(mod 21) = 1, i.e., the period r = d = 3. Hence, log₄(4^x₀) = 0, 1, 2 is obtained. The number of qutrits used in the function register is reduced from 3 to 1. This conclusion switches the control modular multiplication to the TCNOT shown as^[13]

Above all, figure  1(b) shows the implementation of Theorems 2 and 3.

Note that the scalability of the Theorems 2 and 3 is based on a certain circumstance, i.e., N and a are pre-determined. With the presence of such a precondition, we can classically compute other parameters, such as r and d, to design experiments.

The two-qutrit quantum circuit in Fig.  1(b) can be achieved in two ways: separately implement the three gates step-by-step or implement the whole algorithm in one step. In the following Section  3, the two-qutrit system is encoded into the nine lower vibrational states of an ion trapped in anharmonic potential. Similarly to the TCNOT, H⁽³⁾ and InvH⁽³⁾ should be expanded by adding the needed identity matrix to create the 9× 9 matrices: H⁽³⁾ ⊗ I⁽³⁾ and InvH⁽³⁾ ⊗ I⁽³⁾. The three unitary operation can be applied to the two-qutrit system step-by-step, or the whole order-finding algorithm can be represented by a single 9× 9 unitary matrix: U = (InvH⁽³⁾ ⊗ I⁽³⁾)· TCNOT· (H⁽³⁾ ⊗ I⁽³⁾). The final result is

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Quantum circuit for the order-finding algorithm. (a) Ternary order-finding algorithm for factoring 21 with order 3, and the positive integer, which is a co-prime to 21, is randomly chosen to be 4. (b) Simplified circuit.

Considering one single ion trapped in a Paul trap. The radio-frequency electrodes have an oscillating voltage applied to them, the others are applied with static voltages. The trapping potentials are arranged such that the ion is confined more strongly in the radial directions than in the axial direction.^[20] Such a system is essentially one-dimensional. The position of the ion is given by axial coordinate z, measured here in the atomic units of length (which is the Bohr radius, r₀). In the harmonic potential trap it is well-known that the frequencies between different energy levels are all the same. After a slight anharmonic potential is added, selectively addressing and controlling the transitions between two specific energy levels of the ion become feasible by applying a spatially homogeneous field with time-dependent amplitude ε (t).^[19] Traditionally, the analytical anharmonic potential has the form of ϕ = kz²/2 + k′ z⁴/4!, ^[20] where the coefficients k and k′ represent two force constants. The parameters used in this paper are determined by mimicking the previous studies, ^{[19, 27]} where a ¹¹¹Cd⁺ ion is trapped with the axial (harmonic) frequency of ω /2π = 2.77  MHz. According to k = mω ², 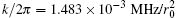. The anharmonic term is chosen.

Based on the above parameters, energy eigenvalues of the lower ten vibrational states (E) and transition dipole moments (the bold numbers) are calculated and summarized in Table  1, which are then used in the following OCT calculation. Details of the calculation can be found in Ref.  [27]. Although the added anharmonicity is relatively small, the effect of anharmonicity can be easily spotted from the transition frequencies. The transition frequency for excitation of one quantum of vibration increases as the vibrational state number increases. For example, for a single excitation of the lowest vibrational state the frequency is ω _{0, 1}/2π = 2.8151  MHz, while for the 10th state it is ω _{9, 10}/2π = 3.1224  MHz, which is about 10.9% higher. A transition dipole moment is used to measure the transition degree between states v and v′ , which can be calculated as M_{v, v′} = 〈 Ψ _v(z)| qz| Ψ _v′ (z)〉 , where Ψ _v(z) is the wave function of state v. Note that the dipole moments are clearly dominated by transitions, as shown in Table  1, which is consistent with the slight anharmonicity of the system. For example, the matrix element M_{0, 1} = 30.3181er₀ is two orders of magnitude larger than the element M_{0, 3} = 9.47× 10^{− 2}er₀, which in turn is two orders of magnitude larger than M_{0, 5} = 4.98× 10^{− 4}er₀. In the whole paper, the two-qutrit system is encoded into the nine lower vibrational states, as shown in the first row of Table  1. The 10th abundant state (| unused〉 ) is also involved to avoid reflection of the upper states.

Table 1

Table 1

Table 1 Relevant vibrational energy levels and transition dipole moments for ten lower vibrational states in the model system of an ion trapped in weakly anharmonic potential. The qutrit state assignments are shown in the first row. The energies of eigenvalues E/2π are in units of MHz. The values of the dipole moment are in units of er0. Qutrits state | 00〉 | 01〉 | 02〉 | 10〉 | 11〉 | 12〉 | 20〉 | 21〉 | 22〉 unused v: vibrational 0 1 2 3 4 5 6 7 8 9 state E/2π 1.3964 4.2115 7.0702 9.9707 12.9115 15.8910 18.9079 21.9611 25.0494 28.1718 0 1.3964 0.0000 30.3181 0.0000 0.0947 0.0000 0.0010 0.0000 0.0000 0.0000 0.0000 1 4.2115 30.3181 0.0000 42.5473 0.0000 0.1806 0.0000 0.0010 0.0000 0.0000 0.0000 2 7.0702 0.0000 42.5473 0.0000 51.7310 0.0000 0.2729 0.0000 0.0020 0.0000 0.0000 3 9.9707 0.0947 0.0000 51.7310 0.0000 59.3217 0.0000 0.3697 0.0000 0.0030 0.0000 4 12.9115 0.0000 0.1806 0.0000 59.3217 0.0000 65.8878 0.0000 0.4693 0.0000 0.0040 5 15.8910 0.0010 0.0000 0.2729 0.0000 65.8878 0.0000 71.7235 0.0000 0.5707 0.0000 6 18.9079 0.0000 0.0010 0.0000 0.3697 0.0000 71.7235 0.0000 77.0050 0.0000 0.6730 7 21.9611 0.0000 0.0000 0.0020 0.0000 0.4693 0.0000 77.0050 0.0000 81.8477 0.0000 8 25.0494 0.0000 0.0000 0.0000 0.0030 0.0000 0.5707 0.0000 81.8477 0.0000 86.3323 9 28.1718 0.0000 0.0000 0.0000 0.0000 0.0040 0.0000 0.6730 0.0000 86.3323 0.0000

Table 1 Relevant vibrational energy levels and transition dipole moments for ten lower vibrational states in the model system of an ion trapped in weakly anharmonic potential. The qutrit state assignments are shown in the first row. The energies of eigenvalues E/2π are in units of MHz. The values of the dipole moment are in units of er0.

In order to obtain the electric field ε (t) for transferring from a given initial state Ψ _v(z) to a chosen target vibrational state Ψ _v′ (z), or to a superposition of states ∑ c_v′ Ψ _v′ (z), the OCT of Rabitz^{[28, 29]} is employed to maximize the objective functional

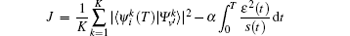
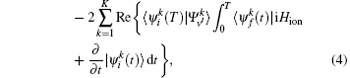
where ψ _i(t) and ψ _f(t) are the time-dependent wave functions driven by ε (t) forward and backward, respectively. The first term in Eq.  (4) represents an overlap of the final wave function with the target state and it is maximized; the second term is required to minimize energy of the field and constrain its smooth switching on and off; and, the last term ensures that evolution of the wave functions satisfies the time-dependent Schrö dinger equations i∂ ψ ^k(t)/∂ t = H_ionψ ^k(t), where

The electric

permits one to determine the optimal ε (t) iteratively.

We start with a guess electric (Asin(| E_v′ − E_v| t) sin²(π t/T)) and improve its shape iteratively by propagating the time-dependent Schrö dinger equations forward and backward in time until the convergence is achieved. At the end of each backward propagation, new values of the electric field are updated and then used for the forward propagation, as well as in turn. The initial and target states of forward and backward propagation are mutual. Note that propagation performance depends somewhat on the penalty factor α .^[30] In the following numerical calculations in Section  5, the wave packet is expanded in the basis set of ten vibrational eigenstates. The amplitude of the guess pulse A is set to 10  mV/cm, penalty factor α is chosen to be between 1× 10¹² and 4× 10¹². The number of forward– backward iterations for convergence is set to 10000.

Usually, multiple state-to-state transformations are optimized simultaneously. For example, for a TCNOT gate (in Fig.  1(b)) we have to find a universal pulse to induce simultaneously nine transitions between the state pairs, which are shown in Eq.  (2), i.e., | 11〉 → | 10〉 , | 20〉 → | 22〉 , and so on. In practice, the accuracy of the obtained pulse is assessed by the cumulative transition probability , which is the first term in Eq.  (4). Another quality used to assess the optimized pulse is gate fidelity: . Note that in the F expression different overlaps are added coherently, which takes into account the phase information. One way of enforcing the global phase alignment in the OCT calculations is to add one more superposition transition to the training set.^[31] Such a superposition state transition is utilized in Section  5.3 to implement the ternary Shor’ s algorithm.

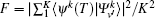
The ternary Hadamard gate (H⁽³⁾ ⊗ I⁽³⁾) and TCNOT (Eq.  (2)) are separately implemented and analyzed in Sections  5.1 and 5.2. They are the elemental gates of the improved ternary Shor’ s order-finding quantum circuit (Eq.  (3)), which is then implemented and analyzed in one step in Section 5.3.

5.1. Ternary Hadamard gate

The first stage of order-finding is applying a ternary Hadamard gate to the argument register initially in the state | 0〉 and the function register is uninfluenced, i.e., . The encode scheme is shown in Table  1. The field optimized for H⁽³⁾| 00〉 is shown in Fig.  2(a). Several calculations are carried out with different T values. When the optimal duration of the pulse set to 15 μ s, P = 0.9991 are obtained. The field amplitude does not exceed 6.5  mV/cm. The envelope of the pulse is smooth; however, the pulse shape is complicated. Thus, a standard technique of the FFT (fast fourier transforms) is employed to analyze the frequency content of the pulse. Figure  2(b) shows the spectrum in frequencies. It exhibits a primary spectral structure that covers | 00〉 → | 01〉 , | 01〉 → | 02〉 , ..., | 12〉 → | 20〉 transitions, which are shown with dotted lines correspondingly.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Optimally shaped 15  μ s pulse for ternary Hadamard gate implemented in the model system. (b) Results of Fourier transform of the optimized pulse.

The frequency spectrum clearly corresponds to control of the ladder state transformations which are shown in Fig.  3. In this case, the population of the initial state | 00〉 should be transferred in equal amounts to the three final states. In the first 5  μ s the decrease of population of state | 00〉 mirrors the increase of population of state | 01〉 . Then, state | 02〉 starts receiving population from state | 01〉 , thus the population of state | 02〉 increases while that of state | 01〉 decreases. Such phenomenon is still demonstrated by the following consecutive state pairs. This is achieved by inducing a ladder of consecutive state-to-state transitions, which is based on the dipole moments summarized in Table  1. At the end of the pulse, each of the final states is expected to receive the population of 1/3 and the middle states are back to zero. Figure  3(b) shows the time evolution of population in the three upper vibrational states, which are shown in logarithmic scale. At this scale the curves in Fig.  3(b) exhibit some negligible residual population compared with that in Fig.  3(a). Figure  3(c) shows the average probability and the fidelity of the gate for transforming the initial state | 00〉 , i.e., K = 1. Therefore, they exhibit the same convergence characteristic.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Ternary Haramard gate in the model system. (a) Switching of population between the qutrit states during . (b) Populations of the three upper vibrational states during the ternary Haramard gate remain small and their residual populations are negligible. (c) Fidelity and average probability of the gate.

5.2. TCNOT gate

The second stage of order-finding is to apply the TCNOT gate to the registers contain the outputs of the first stage. According to Eq.  (3), nine transformations should be involved simultaneously in the field optimization. In addition, it should also be remembered that quantum system can be in any superposition of these states, and the field pulse should also be able to transform appropriately the superposition state. This is absolutely necessary to increase the fidelity of control since a common phase is enforced for all transitions and the resultant field pulse is indeed capable of carrying out a unitary and coherent transformation of any arbitrarily chosen state.^[31] Hence, ten transformations, including an extra equally weighted superposition of states

are optimized simultaneously.

Figure  4 shows the state to state transitions which can be divided into four representative categories: (i) The first three columns in Eq.  (3) are typical since they are similar to the identity matrix. However, from Figs.  4(a)– 4(c) we can see that the transitions from the initial states to themselves are not straight forward. In Fig.  4(a), the population in states | 00〉 and | 01〉 are nearly 0.1 and 0.9 at about 20  μ s, respectively. However, they return to the initial values at the end of the pulse duration. Figures  4(b) and 4(c) show the same phenomenon, while the probability variations during | 02〉 → | 02〉 in Fig.  4(c) is smaller. (ii) Probabilities exchange between adjacent states, which are shown in Figs.  4(e)– 4(h). In Fig.  4(e), probability of state | 11〉 is equal to 1 at the beginning. During the pulse its probability decreases and the probability in state | 10〉 increases. The lower vibrational state | 02〉 also increases slightly and then returns back to zero at the end of the action. (iii) Transitions characterized by . Figures  4(d) and 4(i) are the attribute of this category. According to Table  1, the dipole moments are clearly dominated by odd step transitions. Such a property suggests that two quanta of vibration in the model system might be easier to achieve by introducing a ladder of consecutive state transitions. For example, figure  4(d) shows that in the first 20  μ s of the pulse action, transition is induced and population of the initial state | 10〉 is converted almost entirely into population of the state | 11〉 . Then, transition to state | 12〉 starts showing up and the increase of population in state | 12〉 mirrors the decrease of population in state | 11〉 . (iv) The evolution of the superposition state, which is shown in Fig.  4(j).

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. State transitions of the TCNOT gate in the model system. (a)– (i) Switching of population between the two-qutrit states during the evolution according to Eq.  (3). Note that only the states with population variation are shown. Populations of the other states in each window are small and negligible since they are the same scale with that in Fig.  3(b). (j) Population switching during the evolution of the equally weighted superposition of states.

A convergence study is carried out to make sure that the results are reliable. Figure  5(a) shows the average transition probabilities of forward and backward propagations of the TCNOT gate. The results converge within about 6000 iterations. Both transitions are controlled up to 0.998. Figure  5(b) shows the gate fidelity, 0.965, which is lower compared to the corresponding P caused by the phase error.^[31] The optimized pulse is summarized in Fig.  6, which is simple with the maximum amplitude about 2.5  mV/cm. Such an amplitude scale is easy to achieve in experiments. The frequency contents of the pulse are analyzed in this subsection. According to Fig.  4, primary transitions occur between state pairs | 00〉 and | 01〉 (Figs.  4(a) and 4(b)), | 02〉 and | 10〉 (Figs.  4(c) and 4(e)), | 10〉 and | 11〉 (Figs.  4(d) and 4(e)), | 11〉 and | 12〉 (Figs.  4(d) and 4(f)), | 20〉 and | 21〉 (Figs.  4(g) and 4(i)), and | 21〉 and | 22〉 (Figs.  4(g)– 4(i)). The six analytical transition frequencies (Table 1) are shown with red dotted lines. In practice, the frequency spectrum of the obtained pulse is slightly different (see Fig.  6(b)). However, six crests in the primary spectrum are distinct. This happens because the ladder of consecutive state transition is not as strict as the presence of the dipole moment between state indexes ± 3, ± 5.

Fig.  5.

	Figure Option ViewDownloadNew Window
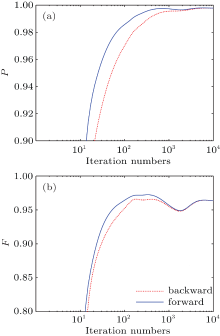	Fig.  5. (a) Average probability of the TCNOT gate. (b) Fidelity of the gate as a function of iteration numbers.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) Optimally shaped 40  μ s pulse for the TCNOT gate implemented in the model system. (b) Results of Fourier transform of the optimized pulse.

Up to now, the gates, H⁽³⁾ ⊗ I⁽³⁾ and TCNOT, in Fig.  1(b) have been achieved independently. A straightforward way to implement the ternary quantum algorithm is orderly applying the optimized pulses obtained in Sections  5.1 and 5.2 to the ion trapped in the model system. The InvH⁽³⁾ can be achieved in the same way as introduced in Section  5.1. There is a drawback of such serial manipulation: phase alignment between the gates would be critical and may limit the fidelity of the optimization. This problem can be alleviated by implementing the entire quantum circuit in one single step, which is introduced in detail in the following Section  5.3.

5.3. Ternary Shor’ s order-finding

The entire ternary quantum order-finding algorithm, i.e., equation  (4), is implemented in one single step. In order to compare the optimization performance with and without involving the equally weighted superposition of states transition , we have implemented two groups of optimization. The average probabilities and fidelities are summarized in Fig.  7. The results converge within about 3000 iterations. For the transformations of the two different training sets, the characteristic probabilities are 0.9943 and 0.9919, respectively, which are shown in Figs.  7(a) and 7(b). However, there is a tremendous difference in the characteristic fidelities. The fidelity in Fig.  7(c) is low (maximum 0.17) due to the serious phase error, while it increases to 0.9630 after introducing the superposition state transition. This conclusion validates the feasibility of the method proposed in Ref.  [31] to enforce the global phase alignment in the OCT calculations. Although such fidelity is not very high, in our opinion, this is favorable, taking into account the number and complexity of the state transformations.

Fig.  7.

Figure Option ViewDownloadNew Window

Fig.  7. (a) Convergence of iterations and average probabilities of the ternary order-finding algorithm without involving the equally weighted superposition of states transition. (b) Convergence with involving the equally weighted superposition of states transition. (c) Fidelity of pulse for simultaneously optimizes nine state transformations. (d) Fidelity of pulse for simultaneously optimizes ten state transformations.

In the following, we analyze the state-to-state transitions. According to Eq.  (4), each initial state should be transferred in equal amount to all of the nine states. Thus, all of the final states are expected to receive the population of 1/9 at the end of evolution. In addition, the evolution of each of the state populations is similar. We analyze the population transformation of initial state | 00〉 for clarity. Another reason for selecting the state | 00〉 is that such a state is actually the input state of Shor’ s algorithm.^[12] The evolution of the equally weighted superposition of states is similar to Fig.  4(j), we do not repeat it again.

The evolution of | 00〉 is shown in Fig.  8. In the first 12  μ s, the decrease of population of state | 00〉 mirrors the increase of population of state | 01〉 . During the time interval near t∼ 12– 20  μ s, the decrease rate of state | 00〉 becomes larger than the increase rate of state | 01〉 . The corresponding population variations are 0.5296 and 0.3692, respectively. This means that state | 01〉 receives less population than that which state | 00〉 releases. This population gap is transferred to state | 02〉 from state | 01〉 . It can be seen from this that state | 02〉 starts receiving population at about t = 12  μ s, which is earlier than the maximum population of state | 01〉 shows up. According to Table  1, the dipole moment between upper states transition is larger than that of lower states, such as the matrix element in Table  1  M_{1, 2} = 42.5473er₀ is larger than the element M_{0, 1} = 30.3181er₀. In addition, although the dipole moment for transition is small, it still attributes the population transfer. These two reasons mean that the ladder of consecutive state transition is not very strict. For example, state | 10〉 starts receiving population at about t = 17, which is also earlier than the maximum population of state | 02〉 shows up. The same scenario repeats again and again for the following vibrational states transferring. State | 11〉 starts receiving population at t = 20, | 12〉 start at t = 23.5, ..., | 22〉 start at t = 35. During the time interval near t ∼ 20– 40  μ s, the population oscillates between the nine encoded states. At the end of the optimization, the final populations of all of the encoded states are all equal 1/9. Note that | unused〉 state is expected to be unpopulated, which is shown in Fig.  8 with a scale of 10^{− 7}.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. Time evolution of state | 00〉 of the ternary Shor’ s order-finding algorithm.

The optimized field is shown in Fig.  9(a). The duration of the pulse is 50  μ s, which is well within the limits of typical coherence time in the modern ion traps (100  ms range^[1]). The maximum amplitude is 4.5  mV/cm. Frequency contents are also primary interested. According to Fig.  8, all of the nine encoded states are involved in the ladder of population transition. Figure  9(b) shows a primary spectral structure that covers the eight transition frequencies. Similar to Fig.  6(b), eight analytical transition frequencies (Table  1) are shown with red dotted lines. In practice, the frequency spectrum of the obtained pulse is also slightly different to the analytical values. However, eight crests in the primary spectrum are evident. This happens because the ladder of consecutive state transition is not very strict.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. (a) Optimally shaped 50  μ s pulse for the ternary order-finding algorithm implemented in the model system. (b) Results of Fourier transform of the optimized pulse.

In this paper we have explored the scalability of quantum computing in higher-dimensional Hilbert space. Since a bigger space enables us to significantly reduce the required number of elemental gates, a ternary Shor’ s algorithm for specifically factorizing 21 is implemented using two qutrits. The two-qutrit quantum circuit consists of only three gates, which is encoded into the vibrational states of a single ion trapped in anharmonic potential. Such a trapped ion system is an appropriate model to study higher-dimensional quantum computing. In the model system an optimal control theory is employed to achieve the specific ternary Shor’ s algorithm in one step. Our numerical simulation results show that accuracy of 0.9919 is achieved. A larger number of iterations would improve the accuracy of the transformation even further. Although the implementation of the ternary algorithm is aiming at a small number, it is still a necessary step on the path towards scalable quantum computing.