Cite this Article
Qi Yue-Ying, Ye Dan-Dan, Wang Jian-Guo, Qu Yi-Zhi. Fast-electron-impact ionization process by 3p of hydrogen-like ions in Debye plasmas* . Chinese Physics B, 2015, 24(3): 033403  
Permissions
Fast-electron-impact ionization process by 3p of hydrogen-like ions in Debye plasmas*
Qi Yue-Yinga)†, Ye Dan-Dana), Wang Jian-Guob), Qu Yi-Zhic)
School of Mathematical & Physics and Information Engineering, Jiaxing University, Jiaxing 314001, China
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
College of Material Sciences and Optoelectronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China

†Corresponding author. E-mail: yying_qi@mail.zjxu.edu.cn

*Project supported by the National Basic Research Program of China (Grant No. 2013CB922200) and the National Natural Science Foundation of China (Grant Nos. 11005049, 11025417, and 10974021).

Abstract

The plasma screening of fast-electron-impact-ionization by excited state (3p) of Hydrogen-like ions was investigated in the first Born approximation with a plasma screening length δ varying from 1000 a0 to 10 a0. The generalized oscillator strength densities showed dramatic changes: some accessional minima occurred along with a remarkable enhancement in certain continuum-energy domains. The double-differential cross sections exhibit not only the same structures as the Bethe surface for moderate and large momentum transfers, but also a broadened enhancement for small momentum transfers. The single-differential cross sections exhibit a near-zero-energy-enhancement and prodigious multiple-shape resonances, depending on the continuum energy and the plasma screening length. These features are analogous to those of the photo-ionization cross section. These findings, for both types of cross section, can be explained by processes associated with continuum electrons, as long as the potential has a short-range character.

Keyword: 34.80.Dp; 52.20.–j; near-zero-energy enhancement; multiple shape resonance; differential cross section; Bethe surface
1. Introduction

Electron-impact ionization processes are used in a diverse range of fields, such as radiation physics, plasma physics, atmospheric physics, astrophysics and electron microscopy, [1] and have been subject to numerous theoretical[2– 10] and experimental[11– 15] studies. In recent decades, high-resolution measurement has made high-order interaction terms discernible, especially in extreme conditions such as plasma environments and strong electric, magnetic, or laser fields, etc. In hot dense plasma, many theoretical investigations[16– 25] and experimental studies[26, 27] have been performed on plasma-screening effects on atomic structure and spectra, [17, 28] and several of dynamic processes. Photo-ionization, [18, 29– 31] and electron-impact excitation with hydrogen-like ions are investigated using the convergent-close-coupling method, [22]R-matrix method, [20] the first Born approximation, [19] and the first-order semi-classical SL trajectory approximation.[32] However, studies on fast-electron-impact ionization are seldom performed because of excessive partial-wave contributions and the inherent difficulty in carefully computing continuum wave functions.

If an incident electron is fast enough, the Bethe– Inokuti theory[2, 3] can be applied, where the expression for the double-differential cross section (DDCS) can be expressed as two distinct factors:[2] one dealing with the incident electron and the other dealing with the target, which is the generalized oscillator-strength density (GOSD) of an atom or molecule. The single-differential cross sections (SDCS) for the high-energy-electron-impact ionization are finite but not zero at the ionization-threshold for the pure-Coulomb potential. However, the most prominent manifestations of non-Coulomb character for the self-consistent field are the shape resonances and zero values at the ionization threshold from the Winger threshold law. The shape resonances emerge due to the centrifugal barrier in the effective potential of the continuum channel ε l′ when l′ > 0, and the zero values appear at the ionization threshold due to the local potential. In the present paper, the interaction between charged particles is local because of plasma screening, and thus we can predict that these characteristics will account for the electron-impact ionization process in a plasma environment. In a previous paper, [32] we studied the plasma effect on fast-electron-impact-ionization by 2p state of hydrogen-like ions in the Debye– Hü ckel potential

which denotes the interaction between an ion of positive charge Z and an electron, where is the Debye screening length, kB is the Boltzmann constant, and Te and ne are the electron temperature and density, respectively. The interaction potential  (1) is accurate if the Coulomb coupling parameter Γ = e2/akBTe ≤ 1, where a = (3/4π ne)1/3 is the average inter-particle distance, and the non-ideality parameter γ = e2/DkBTe < 1. However, the highly excited states are more important for plasma diagnostics because of their relatively high population.

The purpose of this paper is to investigate plasma screening on fast-electron-impact ionization with 3p for hydrogen-like ions in the first Born approximation (FBA). The calculation details can be found in our previous papers[17– 19, 31, 33] and will not be given here for the sake of brevity. In the remainder of this paper, we will present and discuss the characteristics of GOSD, DDCS, and SDCS for the ionization process involving 3p state. Atomic units will be used for the remaining sections unless otherwise explicitly stated.

2. Results and discussion
2.1. Generalized oscillator strength density

Following Ref.  [33], the GOSD in Debye plasmas is given as

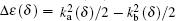
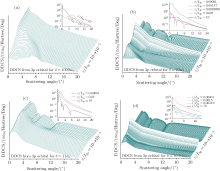
where Δ ε (δ ) = ε (δ ) − ε nl (δ ) = ε (δ ) + I(δ ) is the Z-scaling transition energy by the transformation δ = ZD, ε (δ ) = E(Z, D)/Z2, from the initial channel | nl〉 to the final channel | ε l′ 〉 . According to the energy conservation, is the energy transfer, where ka and kb are the Z-scaling momenta of the incident electron and scattered electron, respectively. Based on our previous research, [17– 19, 31, 33] we can predict that this quantity will be influenced by the plasma-screening effect because it effectively changes the atomic wave functions (both bound and continuum) and the atomic ionization energies.

GOSD can be represented comprehensively by a three-dimensional plot of dfGOSD(q(δ ))/dε as a function of ln (q2(δ )) and ε , called the Bethe surface, [2] which embodies all information concerning the inelastic scattering of charged particles by an atom or molecule within the first Born approximation, and proves useful for an analysis of quantities such as stopping power and total-inelastic-scattering cross section. The Bethe surface for the pure Coulomb field is separated into two distinct domains[2] depending on energy transfer, and possesses a regular ridge in the larger energy-transfer domain, which is common to all atoms and molecules and is independent of the atomic or molecular inner structure. However, the Bethe surface is sensitive to the electronic structure of an individual atom or molecule for smaller energy-transfer domain, which corresponds to a lower continuum energy ε , whose wave function is largely dependent on the atomic potential, resulting in a considerable difference between the plasma environment and the pure Coulomb field.

The Bethe surfaces from the excited state 3p are plotted in Fig.  1 for δ = 1000a0, 20a0, 10a0. In this work, we replace the unscreened case with the case where δ = 1000a0, because we have already established that the plasma effect is practically negligible on the atomic energies and wave functions in this plasma. In the unscreened case, there is a Bethe ridge followed by a series of hips in the GOSD for 3p from the ionization threshold to the larger continuum energy, as shown in Fig.  1(a). The position and the value of these hips are regularly arrayed as functions of ε /I3p and momentum transfer ln (q2), as shown in the inset of Fig.  1(a). This feature is similar in the 2s orbital but different for the 2p orbital, [33] and is attributable to the node of the wave functions for 3p and 2s states.

Fig.  1. A model of the Bethe surface from the 3p excited state for hydrogen-like ion in Debye plasmas. The horizontal axes for ε /I3p and the momentum transfer ln q2 define the base plane. The vertical axis represents the generalized oscillator strength density. The energy range for the continuum electrons is ε /I3p = 10− 5 ∼ 10.

In a plasma environment, the bound and continuum wave functions vary considerably due to the screening potential, the zero-energy enhancement, and the shape resonance, to produce the above-threshold domain (green lines) and the resonance domain (red lines) in the Bethe surface; the case where δ = 20a0 is a typical example, as shown in Fig.  1(b). In the above-threshold domain, three accessional minima emerge in the Bethe surface, and move towards the larger momentum transfer with an increasing energy of electronic ejection. In this energy domain, only the s wave is scattered and other partial waves are forbidden. Owing to the centrifugal barrier, there are three zeros for the transition (ltl′ ) = (110) and these zeros are all observed in the screened case, as shown in Figs.  2(a-2) and 2(a-3) for δ = 10a0. Though there are four nodes for the transition (ltl′ ) = (110) in the unscreened case (Fig.  2(a-1)), the contribution from the higher partial waves obscures all but the last node, because the coulomb potential is long-range. The same phenomenon appears for δ = 10a0, as shown in Fig.  1(c).

Fig.  2. Multi-pole transition matrix elements from the 3p excited state in the plasma environment δ = 1000a0, 20a0, 10a0 and for the continuum energy ε /I3p = 10− 5, 2.3695 × 10− 3, 2 × 10− 3, 0.02.

With increasing energy of electronic ejection, the contributions from the higher-angular-momentum states are more and more prominent. No change occurs in GOSD for the unscreened case, but significant changes emerge in the screened case, where only one hip remains, and the Bethe surface spreads outward. The GOSD then has a peak at ε = 4.39726 × 10− 5  a.u. (ε /I3p = 2.3695 × 10− 3), because .[19] In this plasma condition, the f partial wave of the ejecting electron is trapped in the quasi-bound state 4f and its contribution will exhibit a strong enhancement (shape resonance), whose transition matrix elements (ltl′ ) = (123), (143) are represented in Fig.  2(b-3). As a comparison, the other transition matrix elements bearing significant contributions are plotted in Fig.  2(b-2).

Thus, the energy of the ejecting electronic continuum for a single ratio is reduced with stronger plasma screening, in which case the number of final angular-momentum states contributing to GOSD decreases, and the transitions from the lower angular-momentum states becomes predominant. In the common plasma conditions, this contribution decreases progressively with the final angular momentum, becoming large for the same continuum energy. However, when δ approaches (from below) some , the contribution from the final state l′ becomes predominant over all transitions, and shape-resonance and zero-energy enhancement will occur in the high-energy electron-impact ionization process, which changes the photo-ionization process in plasma environments.

2.2. Double-differential cross section

In the previous subsection, we explained GOSDs (Bethe surfaces) and detailed their odd structures. The plasma effect on the double-differential cross section is discussed in this subsection.

A DDCS in the plasma environment can be expression as a function of the GOSD

Obviously, the DDCS is independent of φ . The integration over φ is performed, and thus the DDCS between the scatting angle θ → θ + d θ ,

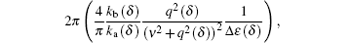
where and ν = 1/δ . The DDCS is exactly the GOSD multiplied by

which yields the contribution from the projectile particle as well as the plasma-screening effect on the projectile particle. The factor q2(δ )/(ν 2 + q2(δ ))2 degenerates to 1/q2(δ ) when ν → 0, namely, the no-plasma-screening case or the free field. For no plasma screening, this factor decreases monotonically with scattering angle increasing proportionally with momentum transfer. However, in plasma conditions, this factor has a maximum near q(δ ) ≈ ν , but is only approximate, because Δ ε (δ )and kb (δ ) are not constant.

When the incident electronic Z-scaling energy is fixed at ε a = 1  keV = 36.76  a.u., it is fast enough for any discrete-level excitation of Hydrogen-like ions, so the first Born approximation can be used. Figure   3 represents the DDCS for 3p with δ = 1000a0, 20.0a0, 11.0a0, 10.94a0, which are divided into three domains: large-angle scattering (third domain), where the DDCS only decreases monotonically; small-angle scattering associated with a large energy transfer (the second domain); and small-angle scattering associated with smaller energy transfer (the first domain). All anomalous structures appear in the first and second domain. In the second domain, when δ = 1000a0 (similar to pure Coulomb scattering), the DDCS begins to decrease from the zero-scattering angle, passes through an extended valley, climbs up to the peak value then down to a hip, and finally enters into the third domain (corresponding to the large scattering angle or the large momentum transfer). Meanwhile, the extend valleys are widened and their magnitudes are reduced with increasing energy of electronic ejection, and the positions of their peaks and hips move toward the large scattering angle. However, in the first domain, the DDCS decreases along a steep gradient slope following the hip because GOSD monotonically decreases before reaching a minimum, while 1/q2(δ ) also decreases with an increased scattering angle, similar to Rutherford scattering.

When δ = 20.0a0, the DDCS in small-angle scattering is separated into three parts, in terms of the energy of electron ejection: the above-threshold domain, the shape-resonance domain (or near-zero-energy enhancement domain), and the large-energy domain. In the above-threshold domain, the DDCS has four broadened enhancements and four minima (corresponding to the pink line from the inset in Fig.  3(b)). The first broadened enhancement and minimum are produced by the factor q2(δ )/(ν 2 + q2(δ ))2, the rest of the minima and the broadened enhancements correspond with positions in the GOSD. The first peak of the first broadened enhancement is located around θ = 0.24258° , corresponding to the momentum transfer 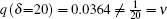when ε = 10− 5I3p, which does not agree with ν because of the singularity of the GOSD in this domain. With the energy of electronic ejection continuously increasing, but in advance of the shape resonance, the contribution from the higher-angular momentum is more and more important. These minima and broadened enhancements are erased, and only one enhancement following a hip remains. In the shape-resonance domain, the transitions (ltl′ ) = (123), (143) dominate the DDCS, whose magnitude increases rapidly. For the larger energy transfer, the DDCSs are similar to the unscreened case and independent of atomic structure.

When δ = 10.94a0, the DDCS resembles the case where δ = 20.0a0, because 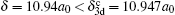. Here, the transitions (ltl′ ) = (112), (132) dominate the DDCS, and their magnitudes increase rapidly. In contrast, figure  3(c) shows the DDCS for , where there is no shape resonance.

Fig.  3. A model of DDCSs from the 3p excited state for hydrogen-like ions in Debye plasmas. (a) δ = 1000a0, (b) δ = 20a0, (c) δ = 11a0, and (d) δ = 10.94a0. The horizontal axes for ε /I3p and the scattering angle θ define the base plane. The vertical axis represents the double-differential cross section. The energy range for continuum electrons is ε /I3p = 10− 5– 10.

Now, we must emphasize that DDCS deceases monotonically with small scattering angles for the plasma-screening interaction, which is the biggest difference from pure Coulomb scattering.

2.3. Single-differential cross section

The single-differential cross section (SDCS) can be calculated from the DDCS as follows:

Using the previous double-differential cross sections, the SDCSs from the excited state 3p for the incident-electron energy ε a = 1  keV at a variety of Debye lengths are shown in Fig.  4. Bracketed values for the critical screening length are chosen in order to demonstrate shape-resonance and zero-energy enhancement in the SDCS, namely, [31] and . The envelopes of the SDCS for high-energy electron-impact ionization are similar to those of the photo-ionization cross section in plasma environments, i.e., exhibiting multiple shape resonance, and near-zero-energy enhancement. However, only the dipole transition happens in the photo-ionization process, and here any-pole transitions are possible, as long as a virtual bound state exists in this plasma condition. It is worth noting that the peaks of the SDCS from 3p and 2p fall at the same continuum state in the same plasma condition, ε = 1.225 × 10− 4  a.u. = 3.33 × 10− 3  eV for δ = 10.88a0 and ε = 8.67 × 10− 5  a.u. = 2.37 × 10− 3  eV for δ = 10.90a0, [33] respectively. The energy position and widths of the resonance peaks within the SDCS are related to the extent of the difference from below, which was demonstrated in the photo-ionization processes in our previous work.[31] The multiple series of shape resonances and near-zero-energy enhancements in the photo-ionization cross section will appear in the SDCS of for electron-impact ionization, as shown in Fig.  4, and their origin and properties are described in Ref.  [31].

Fig.  4. Electron-impact ionization single-differential cross sections for the 3p excited state of Hydrogen-like ions in Debye plasmas with the incoming electron ε a = 1  keV. The energy of electronic ejection ε ranges from the ionization threshold to 10 times the ionization energy.

3. Conclusions

We have studied plasma effects on generalized oscillator strength densities (Bethe surfaces), double-differential cross sections, and the single-differential cross sections from electron-impact ionization in the Debye plasma environments. The results demonstrated that GOSD from the excited state 3p were enormously varied because of plasma-screening interactions, especially near ionization thresholds and with smaller momentum transfers, which corresponding to smaller scattering angles. Accessional minima (hip), broadened peaks, and remarkable augmentation consistently appear in GOSD and DDCS, while multiple shape resonance and near-zero-energy enhancement appear in SDCS, all of which are dependent of the plasma conditions. Although we used the simplest Debye potential to simulate the plasma screening interaction and only calculated the case from the lower orbital, the results have universal significance: the shape resonance and near-zero-energy enhancement will appear in the case of the Rydberg states when the screening interaction is not as strong previously considered, or the screening interactions are not used by the Debye model, but the interaction become local. These effects should be considered in the simulation of spectroscopy for hot, dense plasmas, and are more important for low-energy electron-impact excitation and ionization processes.[20, 22, 34]

Reference
1 Rostas F 1985 Spectral Line Shapes (Vol.  3) New York Walter de Gruyter [Cited within:1]
2 Inokuti M 1971 Rev. Mod. Phys. 43 297 DOI:10.1103/RevModPhys.43.297 [Cited within:5] [JCR: 44.982]
3 Bethe H 1930 Ann. Physik 5 325 [Cited within:1] [JCR: 1.51]
4 http://atom.curtin.edu.au/ccc-ww/index.html [Cited within:1]
5 http://physics.nist.gov/physrefdata/ionization/atom_index.html [Cited within:1]
6 Kim Y K and Rudd M E 1994 Phys. Rev. A 50 3954 DOI:10.1103/PhysRevA.50.3954 [Cited within:1] [JCR: 3.042]
7 Guerra M, Parente F, Indelicato P and Santos J P 2012 Inter. J. M. Spectr. 313 1 [Cited within:1]
8 Tsipinyuk B, Bekkerman A and Kolodney E 2012 Inter. J. M. Spectr. 328 2 [Cited within:1]
9 Wu Y, Wang G Y, Mu Q and Zhao Q 2014 Chin. Phys. B 23 013401 DOI:10.1088/1674-1056/23/1/013401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
10 Liu L J, J C C, Zhang L M, Chen J J and Chen Z J 2013 Chin. Phys. B 22 103401 DOI:10.1088/1674-1056/22/10/103401 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
11 http://www-cfadc.phy.ornl.gov [Cited within:1]
12 Cheng H D, Liu X J, Yuan Z S, Zhu L F, Zhong Z P, Li W B and Xu K Z 2002 Nuclear Phys. Rev. 19 49 [Cited within:1] [JCR: 3.715]
13 Leung K T 1999 Journal of Electron Spectroscopy and Related Phenomena 100 237 DOI:10.1016/S0368-2048(99)00049-3 [Cited within:1] [JCR: 1.706]
14 Sun J M, Zhong Z P, Zhu L F, Li W B, Liu X J, Yuan Z S and Xu K Z 2004 Phys. Rev. A 70 012708 DOI:10.1103/PhysRevA.70.012708 [Cited within:1] [JCR: 3.042]
15 Fan L L, Zhong Z P, Zhu L F, Liu X J, Yuan Z S, Sun J M and Xu K Z 2005 Phys. Rev. A 71 032704 DOI:10.1103/PhysRevA.71.032704 [Cited within:1] [JCR: 3.042]
16 Murillo M S and Weisheit J C 1998 Phys. Rep. 302 1 DOI:10.1016/S0370-1573(98)00017-9 [Cited within:1] [JCR: 22.929]
17 Qi Y Y, Wang J G and Janev R K 2008 Phys. Rev. A 78 062511 DOI:10.1103/PhysRevA.78.062511 [Cited within:3] [JCR: 3.042]
18 Qi Y Y, Wang J G and Janev R K 2009 Phys Rev. A 80 063404 DOI:10.1103/PhysRevA.80.063404 [Cited within:1] [JCR: 3.042]
19 Qi Y Y, Wu Y, Wang J G and Qu Y Z 2009 Phys. Plasmas 16 023502 DOI:10.1063/1.3073675 [Cited within:4] [JCR: 2.376]
20 Zhang S B, Wang J G and Janev R K 2010 Phys. Rev. Lett. 104 023203 DOI:10.1103/PhysRevLett.104.023203 [Cited within:2] [JCR: 7.943]
21 Zammit M C, Fursa D V and Bray I 2010 Phys. Rev. A 82 052705 DOI:10.1103/PhysRevA.82.052705 [Cited within:1] [JCR: 3.042]
22 Zammit M C, Fursa D V, Bray I and Janev R K 2011 Phys. Rev. A 84 052705 DOI:10.1103/PhysRevA.84.052705 [Cited within:2] [JCR: 3.042]
23 Kar S and Ho Y K 2011 J. Phys. B: At. Mol. Opt. Phys. 44 015001 DOI:10.1088/0953-4075/44/1/015001 [Cited within:1] [JCR: 2.031]
24 Jung Y D 1997 Phys. Plasmas 4 21 DOI:10.1063/1.872135 [Cited within:1] [JCR: 2.376]
25 Xie L Y, Jiang J and Dong C Z 2014 Chin. Phys. Lett. 31 023401 DOI:10.1088/0256-307X/31/2/023401 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
26 Goto M, Sakamoto R and Morita S 2007 Plasma. Phys. Controlled Fusion 49 1163 DOI:10.1088/0741-3335/49/8/005 [Cited within:1] [JCR: 2.369]
27 Nantel M, Ma G, Gu S, Côté C Y, Italani J and Umstadter D 2010 Phys. Rev. Lett. 80 4442 [Cited within:1] [JCR: 7.943]
28 Rogers F J, Graboske H C and Harwood D J 1970 Phys. Rev. A 1 1577 DOI:10.1103/PhysRevA.1.1577 [Cited within:1] [JCR: 3.042]
29 Sahoo S and Ho Y K 2006 Phys. Plasmas 13 063301 DOI:10.1063/1.2200290 [Cited within:1] [JCR: 2.376]
30 Sahoo S and Ho Y K 2009 Res. Lett. Phys. 2009 832413 [Cited within:1]
31 Qi Y Y, Wang J G and Janev R K 2011 Eur. Phys. J. D 63 327 DOI:10.1140/epjd/e2011-10570-1 [Cited within:6] [JCR: 1.513]
32 Jung Y D and Yoon Y S 1996 J. Phys. B: At. Mol. Opt. Phys. 29 3549 DOI:10.1088/0953-4075/29/15/024 [Cited within:2] [JCR: 2.031]
33 Qi Y Y, Ning L N, Wang J G and Qu Y Z 2013 Phys. Plasmas 20 123301 DOI:10.1063/1.4833616 [Cited within:5] [JCR: 2.376]
34 Zhang S B, Wang J G, Janev R K, Qu Y Z and Chen X J 2010 Phys. Rev. A 81 065402 DOI:10.1103/PhysRevA.81.065402 [Cited within:1] [JCR: 3.042]