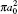†Corresponding author. E-mail: sabbelkilany@yahoo.com
The inelastic collision of protons with sodium atoms are treated for the first time within the framework of the coupled-static and frozen core approximations. The method is used for calculating partial and total cross-sections with the assumption that only two channels (elastic and hydrogen formation in 2s state) are open. In each case, the calculations are carried out for seven values of the total angular momentum ℓ(0 ≤ ℓ ≤ 6). The target is described using the Clementi Roetti wave functions within the framework of the one valence electron model. We use Lipmann–Swinger equation to solve the derived equations of the problem, then apply an iterative numerical method to obtain the code of computer to calculate iterative partial cross-sections. This can be done through calculating the reactance matrix at different values of considered energies to obtain the transition matrix that gives partial and total cross sections. The present results for total hydrogen (2s state) formation cross sections are in agreement with results of other available ones in wide range of incident energy.
The appearance of intermediate states in atomic and nuclear reactions is considered as the most interesting physical phenomenon since the development of quantum theory. The development of femtosecond lasers has tremendously enhanced the experimental identification of these states in chemical and physical reactions. Theoretical investigation on positron– atom or proton– atom scattering has been carried out by many authors. Most theoretical treatments of positron– atom or proton– atom scattering are based on calculations of differential, partial, and total cross sections as functions of incident energy using different approximations. Abdel-Raouf[1] investigated the collision of positrons by lithium and sodium atoms using the coupled static approximation. Elkilany[2– 5] used the variational static approximation or iterative Green's function partial wave expansion method to obtain partial and total cross sections of elastic scattering of positron or electron by inert gas atoms. Surdutovitch et al.[6] reported measurements of Ps formation cross sections for positron collision by lithium and sodium atoms. Jun et al.[7] discussed positronium formation cross sections for positron collision by potassium at low energies using an optical-model method. Roy and Ho[8] calculated the P-partial wave resonance in e+ – Li scattering below the Ps threshold using the stabilization method. Gilmore et al.[9] obtained results for electron– or positron– positronium scattering in low energies using a coupled pseudo-state approximation. Ratnavelu and Ng[10] used the coupled-channel optical method to study positron collision by lithium atom. Abdel-Raouf and Elkilany[11] applied the iterative Green’ s function partial wave expansion method to calculate partial and total cross sections of the collision of positron by helium, neon, argon, and krypton atoms. Abdel-Raouf and Elkilany[12] discussed the appearance of intermediate states (resonant states) in positron– lithium collision. Elkilany[13] computed the partial and total cross sections of excited positronium formation in the scattering of positrons by positronium using the coupled static approximation. Jun et al.[14] calculated the Ps formation cross section in positron collision by lithium atom using the coupled channel optical method. Fang et al.[15] used a coupled-channel optical method to calculate positron collision with lithium atom. Banyard and Shirtcliffe[16] used the continuum-distorted wave method to calculate cross sections for protons scattered from atomic lithium. Ferrante et al.[17] calculated total cross sections for hydrogen formation in protons scattering with alkali atoms using the OBK approximation. Daniele et al.[18] calculated total cross-sections for high-energy proton scattering by alkali atom. Ferrante and Fiordilino[19] investigated high-energy proton collision with alkali atom using the Eikonal approximation. Fritsch and Lin[20] discussed the hydrogen formation in proton scattering by lithium atoms using a modified two-center atomic orbital expansion. Choudhury and Sural[21] calculated the hydrogen formation in the collision of proton with alkali-metal atoms using the wave formulation of impulse approximation. Tiwiri[22] reported the differential and total cross sections in the hydrogen formation in the collision of proton by lithium and sodium atoms using the coulomb projected Born approximation. Elkilany and Abdel-Raouf[23] investigated the effect of polarization potentials on antiproton scattered by positronium using coupled static approximation. Elkilany[24] used the coupled static approximation and Green's function iterative method to calculate partial and total cross sections of anti-hydrogen formation in antiproton positronium collision.
For the first time, we investigate the inelastic scattering of protons by sodium atoms as a two-channel problem in which the elastic and hydrogen (2s state), H(2s), formation channels are open using the coupled-static approximation within the framework of the frozen-core picture of Na atom. The considered method has been applied successfully in the inelastic scattering of proton by lithium atom by Elkilany.[25]
The two-channel scattering problems under investigation can be sketched by
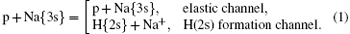
The one valence electron model of an alkali target (Na) is described (in Rydberg units) by[1]
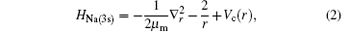
where r is the position vector of the valence electron with respect to the origin of the scattering system, in which the nucleus of the target is infinitely heavy. Vc(r) is a screened potential defined by
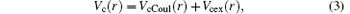
where VcCoul(r) and Vcex(r) are the Coulomb and exchange parts of the core potential.
Following Clementi and Roetti, [26] the wave function of the i-th electron in the orbital j of the target is expanded by
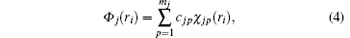
where | χ jp(ri )〉 is a Slater-type wave function given by
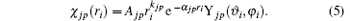
The kjp are integers or zero, Ajp are normalization factors determined by
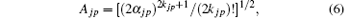
and the spherical harmonics Yjp are normalized by 〈 Yjp(ϑ i, φ i)| Yjp(ϑ i, φ i )〉 = 1. The constants cjp and α jp are adjusted within the framework of the Hatree– Fock– Roothaan approach. Substituting Eq. (5) into Eq. (4) and introducing the notation 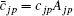
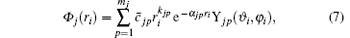
where mj is the number of basis functions characteristic to each orbital. Usually, all the orbitals of the same type have the same mj.
The Coulomb part of the core potential is defined by

where M is the number of orbitals, and Nj is the number of electrons occupying the orbital j. The prime on the sum sign means that the term − 2/r is repeated for each j. The exchange part of the core potential is defined by
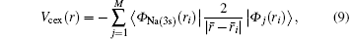
where the subscript Na(3s) is employed for distinguishing the wave function for the valence electron of the target atom.
According to Eq. (2), the binding energy of the valence electron of the target is determined by
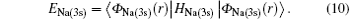
The total Hamiltonian of the first channel, elastic channel, has the following form (in Rydberg units and frozen core approximation):
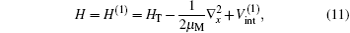
where μ M is the reduced mass of the first channel. In Fig. 1, 

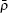
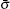
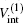
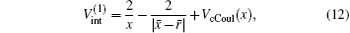
where
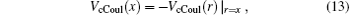
and the corresponding total energy in the first channel is determined by
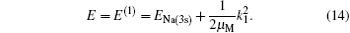
The second term on the right is the kinetic energy of incident proton relative to the target nucleus.
The total Hamiltonian of the second channel, H(2s) formation, is expressed (in Rydberg units and frozen core approximation) as

where μ M′ is the reduced mass of the second channel, 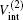
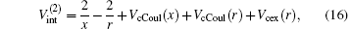
and the total energy of the second channel is determined by
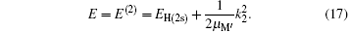
The second term on the right is the kinetic energy of center of mass of H(2s) with respect to the nucleus of the target. This is related to the energy of the incident proton by
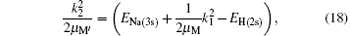
where EH(2s) = − 0.25 Ry is the first excited 2s-state energy of H(2s) and 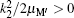
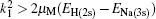
The coupled static approximation states that the solution of the two-channel scattering problem under consideration is subjected to the following conditions:[25]
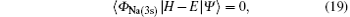
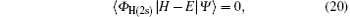
where | Ψ 〉 is the total wave function describing each scattering process, i.e.,
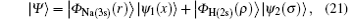
where
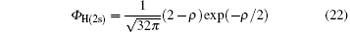
is the ground-state wave function of H(2s), Ψ 1(x) is the wave function describing scattered protons, and Ψ 2(x) is the scattering wave function of the second channel. Substituting Eqs. (14) and (21) into Eq. (19), we obtain

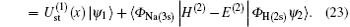
Substituting Eqs. (17) and (21) into Eq. (20), we obtain
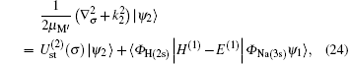
where Schrö dinger’ s equations of the target and H(2s) are employed. The potentials 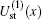
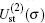


Using the partial wave expansions of the scattering wave functions | Ψ 1〉 and | Ψ 2〉 in Eqs. (23) and (24), solutions are given (formally) by the Lippmann– Schwinger equation (see appendix)
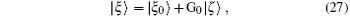
where G0 is the Green operator (ε − H0)− 1 and | ξ 0〉 is the solution of the homogeneous equation
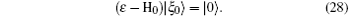
The partial wave expansions of Green operators corresponding to operators in the two differential equations enable us to write their solutions in integral form that can be solved by iterative numerical technique. Then we obtain the reactance matrix Rν which is related to the transition matrix Tν
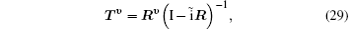
where ν is the order of iteration, I is a 2 × 2 unit matrix, and 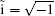
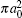
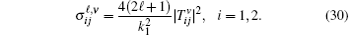
Finally, the total cross sections (in 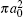

We begin with testing the variation of static potentials of two channels, 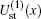
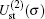
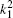
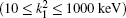
Table 1 shows the partial and total elastic cross sections for all incident values of energy between 10 and 1000 keV. We can conclude the following points: (i) the main contributions to the total elastic cross sections, σ 11’ s, are due to the S and P partial cross sections; (ii) the total elastic cross sections, σ 11’ s, decrease steadily with 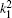
Table 1. Present partial and total elastic cross sections (σ 11 in 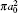 |
In Table 2 we present the partial and total H(2s) formation cross sections, σ 12’ s, at all considered energies. The values indicate that the results shown in Table 1 have been repeated for the values of partial and total H(2s) formation cross sections, σ 12’ s. The most interesting results are accumulated in Table 3, where we find a comparison between total H(2s) formation cross sections (in 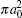
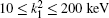
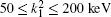
Table 2. Present partial and total H(2s) formation cross sections (σ 12 in 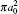 |
Table 3. Present total H(2s) cross-section formation (σ 12 in 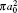 |
It is interesting to mention that all theoretical techniques applied to the collisions of electron with atoms can be extended to proton– atom collisions after allowing for hydrogen formation channel instead of recombination channel. Proton– sodium inelastic scattering is studied using the coupled static approximation. Our interest is focused on the influence of producing H(2s) atom in the second channel. The present calculations of the total H(2s) formation cross sections using the coupled static approximation show a reasonable agreement with available theoretical calculations in a wide region of incident energies.
The author would like to express his deep gratitude to Prof. M. A. Abdel-Raouf for his interest in this work and useful discussion.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|