†Corresponding author. E-mail: ghanbari@phys.ui.ac.ir
The four-body Coulomb–Born distorted wave approximation is applied to investigate the integral as well as projectile angular-differential cross sections for single-electron capture in the collision of energetic singly positive charged helium ions with helium atoms in their ground states. The formalism satisfies the correct boundary conditions. The influence of the dynamic electron correlations on the cross sections is studied by considering the inter electronic interactions in the complete perturbation potentials in post form. Also, the sensitivity of the cross sections to the static electronic correlations is studied by using the single-zeta and the highly correlated Byron–Joachain wave functions to describe the initial bound state of the active electrons. The obtained results for the energy range of 40–5000 keV/amu are reported and compared with other three- and four-body theoretical data and available experimental measurements. The comparison leads us to discuss the validity of the applied approach and survey the interaction effects on the cross sections by recognizing the electron–electron interaction. Particularly, for differential cross sections, the comparison of the present four-body method with the experiment shows that the agreement is not as good as that for its three-body version.
Photon– and ion– atom collisions play a central role in the study of a large number of basic physical phenomena. Among the various categories of scattering systems, heavy ion– atom collisions have been studied extensively.[1– 29] Single electron transfer is an important and sometimes dominant process in a typical heavy ion– atom collision. The importance of this phenomenon in various fields of science has stimulated theoreticial physicists to propose many semiclassical and fully quantum mechanical models for understanding the capture dynamics in different few-body ion– atom collision systems.[2– 19] Both differential and integral cross sections for charge transfer in different ion– atom collisions have been the focus of some experimental researches.[20– 23]
Single-electron capture in the collision of fast singly positive charged helium ions with helium atoms is one of the processes of interest, for which a large number of measured total cross sections exist in the literature.[24– 29] However, the theoretical studies of this process are scarce possibly due to the complexities appearing in the typical five-body problem calculations. The first-order four-body Born approximation with correct boundary conditions (CB1-4B)[15, 16] and the four-body continuum distorted wave approximation (CDW-4B)[15] have been applied to calculate the single electron capture total cross sections for this reaction.
The integrated cross sections provide only an average of the information of the collision dynamics. While, fully differential cross sections contain all relevant information about the collision process and are the most sensitive tests to the validity of theoretical studies. Recently, the novel imaging technique known as cold target recoil ion momentum spectroscopy (COLTRIMS) provides a very efficient way to measure the fully differential cross sections in ion– atom collisions.[1, 20] This development in experimental techniques brings a renewed interest in the theoretical study of the different reactions that may occur in ion– atom collisions at various ranges of the impact energy.
In a previous paper, [7] we calculated the differential and total cross sections for single-electron capture in the collision of fast helium ions with helium atoms in their ground states using a three-body Coulomb– Born distorted wave approximation (CBDW-3B). In that work, the non-captured electrons were considered as the frozen electrons, so their interactions with the active electron were not considered in explaining the capture process. Although, with this three-body approach we obtained comparative success in characterizing the dynamic of the specified collision, it seems that neglecting the dynamic correlations between the involved electrons leads to some unphysical effects in the transition amplitude and to a significant deflection from the experimental data, especially at higher impact energies. On the other hand, there is a widespread belief that an extension of the three-body formalism to its four-body version would give a better description of the considered rearrangement process. The availability of the differential cross sections, the relative success of the CBDW-3B theory in explaining some aspects of the collision process, and the expectation that a four-body version of the formalism may improve the agreement of the results with the experiment, motivated us to generalize our previous calculations to a four-body model.
The present work is aimed at investigating the role of dynamic and non-dynamic electronic correlations for single-electron capture to a projectile ground state without excitation of the target using the four-body Coulomb– Born distorted wave approximation, especially for energetic He+ – He collisions. In order to survey the role of the inter-electron repulsion potential from a dynamic point of view, we employ the post formalism with the concrete full perturbation potential in the exit channel. Also, the sensitivity of the formalism to static correlations is examined using different wave functions to describe the initial bound state of the helium atomic target. The second aim of this paper is a systematic study of the validity of the four-body Coulomb– Born approximation, by comparing the obtained results with the corresponding available experimental data as well as other theoretical calculations.
This paper is organized as follows. In Section 2, we develop and study the basic structure of the present four-body model and briefly sketch the approach to single-electron capture from helium atoms by helium ions as projectiles. In Section 3, the obtained results are presented and compared with those of other theories and the experimental results. The related discussions are also given in this section. Finally, in Section 4, we summarize the results obtained. Atomic units will be used throughout unless otherwise stated.
A four-body collision is considered, in which a projectile ion P with an effective charge of ZP and mass MP captures one electron from a helium target consisting of a target ion T and two active electrons e1 and e2. The mass and charge of the target nucleus are respectively denoted as MT and ZT = 2. Let the position vectors of electron ei (with i = 1, 2) relative to P and T be respectively denoted as xi and si. The inter-electron distance vector is given by r12 = | s1 − s2| = | x1 − x2| . Let the relative vectors of P with respect to the center of mass of the helium target and with respect to the nucleus T be denoted as ST and R, respectively. It is also assumed that during the collision process, electron e1 is captured by the projectile ion and electron e2 remains bound to the target ion. Thus, SP is the relative vector of the center of mass of the newly formed atomic subsystem (P, e1) with respect to the center of mass of the remaining subsystem (T, e2). In the entrance channel, it is convenient to use the set of the Jacobi coordinate vectors 

The exact expressions for the prior and the post forms of the standard transition amplitude for a typical rearrangement process, which are mathematically equal on the energy shell, are given respectively by

where 

In the presence of the two-body Coulomb interactions, for the considered reaction in which the electron of the projectile is not explicitly included (ZP > 1 and ZT = 2), there exists a residual Coulomb interaction between the fragments in the final channel. Consequently, the standard forms of the transition amplitude must be modified to satisfy the correct boundary conditions by including the produced distortion due to this residual Coulomb interaction in the formalism. In the first-order Coulomb– Born distorted wave approximation, the produced distortion is included partially in the final interaction potential and partially in the corresponding asymptotic wave function to satisfy the proper boundary conditions. Consequently, the modified forms for the matrix elements of the amplitudes, in the first-order approximation, are given by

in which

where 

Therefore,

where η = μ f(ZP − 1)/Qf is the final Coulomb repulsive or Sommerfeld parameter, Qi and Qf are the initial and final wave vectors for the relative motion in the center of mass frame, 1F1(a; b; x) and Γ (x) are respectively the confluent hypergeometric and Euler’ s gamma functions.
In Eq. (3), E is the total energy of the system and is given by

where ϵ i and ϵ f are the initial and final bound-state energies, and μ i and μ f are the reduced masses of the two aggregates in the entrance and exit channels,

with m being the mass of the electron. The other reduced masses are defined as

For computational purposes, the following initial bound-state wave function is used:

in which 𝒩 i, 

in which the normalization factors 𝒩 P and 𝒩 T are respectively given by 

Substituting the explicit forms of the distorted initial and final perturbation potentials, Ui and Uf, as well as the asymptotic initial and final wave functions, ϕ i and ϕ f given in Eq. (4), into Eq. (2) leads to the following integral forms for the CBDW-4B matrix elements of the transition amplitude:

in which the partial transition amplitude 𝓘 S (S = R, x1, x2, s1, r12) reads

where 𝒩 = 𝒩 i


When terms of the order m/M (with M = MP and/or MT) are neglected, the position vectors R and SP are approximately equal. This fact has been used to derive the integral forms of the partial amplitudes given in Eq. (8).
Similar to what has been explained in detail in Refs. [9] and [30], the nine-dimensional integral for the partial amplitude 𝓘 R containing the two-body inter-nuclear Coulomb interaction can be reduced to a one-dimensional integral which is easy to calculate numerically. Toward this end, the integration over s2 can be easily performed as

Now, applying the integral identity

and using the fact that x1 = s1− R, we derive

By noting that

the result

is obtained. Using the Feynman identity[31]

we have

in which 

we obtain

Similar to that for the three-body rearrangement processes discussed in Ref. [9] and [30], and using the Nordsieck integral, [32] the final one-dimensional integral form of 𝓘 R is obtained as

where

Proceeding in a similar manner, we may also reduce the nine-dimensional integrals for 𝓘 x1 and 𝓘 s1 to the one-dimensional integrals as follows:


In order to reduce the partial transition amplitude 𝓘 x2 to a two-dimensional integral, the s2 integration can be simplified using the Fourier transform of e− σ s2 and employing the Feynman identity. A simple manipulation yields

in which ρ 2 = y[σ 2 + (1 − y)q2]. Using this result together with the integral identity (10), and performing the s1 integration as is carried out in Eq. (12), we obtain

Again, by using the Feynman identity (14), the k integration can be performed to obtain


The R integration is a special case of the Nordsieck integral and has a closed form. Inserting the analytical expression for this integral into the above equation results in the following final form for 𝓘 x2:

A similar procedure can be developed to reduce the partial transition amplitude 𝓘 r12 to a two-dimensional integral. The result is

where 
Both differential and integral cross sections for single-electron capture in the collision of singly positive helium ions with helium atoms can be calculated using the post and/or the prior transition amplitudes given in Eq. (7). In the center of mass (c.m.) frame, the differential cross section is given by

and the integral capture cross-section is given by

where 𝒯 if is the prior or post transition amplitude and θ is the scattering angle.
Finally, we note that the projectile carries an electron with a given spin projection, and the Pauli principle will prevent an electron with like spin to be captured (unless an excited state is formed). This means that for the 1s → 1s transition, the two ground-state electrons of the helium target are not equivalent; while for the transitions from the 1s state to all excited states, these electrons can be considered as equivalent electrons. Subsequently, using the well-known n− 3 scaling rule, we estimate the total cross sections for capture to all the possible final states as 
The main intent of the present study is two-fold. First, the model is meant to demonstrate the influence of the static and dynamic electron correlations on the differential cross sections by directly comparing the obtained results with their corresponding experimental measurements as well as the results of other theories. Second, we would like to determine whether a generalization of the CBDW-3B approximation to a four-body formalism improves the results for differential cross sections. To this end, in this section, the obtained results for single-electron capture in the collision of singly positive helium ions with helium atoms in their ground states are presented and discussed. The following results are obtained using the single-zeta wave function (SZ):[34]

with

which describes the initial bound state of the two electrons in the helium targets. In the following discussion, we assert that the CBDW-3B theory deals with the specified problem as a symmetric collision system for which ZP = ZT. It is well known that the prior and the post forms of the transition amplitude are equal for symmetric collisions. In our previous study, [6] two sets of results obtained with different effective nucleus charge numbers were discussed. However, since the CBDW-3B theory with the effective nuclear charges of ZP = ZT = 1.339 gives a better description of collision dynamics, in the following figures only these results are depicted and compared with the present calculations. Also, a simple variational wave function is used to describe the ground state of the produced helium atom with ζ P = 1.6875. Consequently, the effective charge number of the projectile ion is assumed to be ZP = 1.6875.
Figure 1 displays the angular distribution of the differential cross sections, obtained from the prior and the post forms of the CBDW-4B transition amplitude, for the collision of 3He+ ions with 4He atoms as a function of the laboratory scattering angle θ lab at an incident energy of 60 keV/amu. In this figure, the results are compared with those of the CBDW-3B and the continuum distorted wave-Born initial state (CDW-BIS) approximations.[6, 20] The experimental values obtained by Schö ffler et al. are also depicted in the figure to scrutinize the present results. The comparison relates only to the 1s → 1s transition amplitude. One of the basic differences between the CDW-BIS and CBDW theories comes from their distorting potentials. For the CDW-BIS theory, the perturbation potential is an operator-valued potential, whereas for the CBDW theory, the distorting potential is the usual electrostatic Coulomb potential. Although for both of the four-body theories, the initial wave functions are the same as given in Eq. (4), their final wave functions are different. The CDW-BIS employs the scattering wave functions from the CDW-4B method in the exit channel and replaces the Coulomb scattering waves for the relative motion of heavy particles by their asymptotic forms. Considering the differences between the CBDW and CDW-BIS approximations, it is reasonable to expect that they exhibit different behaviors to explain the collision dynamics. However, the accuracy of the models should be examined by comparing those results with experiments.
As is seen from Fig. 1, both the prior and the post formalisms of the CBDW-4B theory show a sharp dip due to the mutual cancelation among the various terms in the perturbation potentials. Here, the angle at which this cancelation occurs is called the dark angle. The dip appearing in the dark angle is unphysical because it may not be observed in experimental measurements. However, in the experimental data, a structure is observed approximately in the same region in which the unphysical dip occurs. For angles below the dark angle, the post CBDW-4B curve lies under both the prior and the CBDW-3B curves. Although the dynamic electron correlation is absent in the prior formalism, it is explicitly included in the post amplitude through the final complete perturbation potential. As is seen from the figure, the maximum difference between the prior and the post results occurs in an angular region before the dark angle. Also it is seen that for extreme forward scattering angles (angles below the dark angle), the post results are in better agreement with the experiment and consequently give a better description of the collision dynamics. Although the effect of the passive electron on the results due to the initial and final bound state wavefunctions is the same in the prior and the post forms of the four-body T -matrix, as the comparison shows, completely neglecting the dynamic correlation may lead to an unphysical behavior of the transition amplitude at extreme forward scattering angles (or large impact parameters). For scattering angles beyond the dark angle, the difference between the prior and the post formalisms is marginal and both have a significant deviation from experimental observations. In this angular region, the CBDW-3B theory is in a better agreement with the experiment. In comparison with CDW-BIS, the present approximation is found to have better agreement with experimental cross-sections compared to the four-body CDW-BIS model for nearly all the considered scattering angles.
The results from the present calculations are given in Fig. 2 for an incident energy of 150 keV/amu. A comparison is made between these results and those obtained from the CBDW-3B and CDW-BIS theories[6, 20] and also those measured experimentally by Schö ffler et al.[20] Here again the explicit inclusion of the dynamic correlation would lead to better results at angles around the zero scattering angle. For this case, the post, prior, and CDW-BIS curves coincide with each other at larger scattering angles. In an angular region above the dark angle, the difference between the results obtained from the four-body theories and the experiment is considerable. Also, near the region of the dark angle, a structure appears in the experimental measurement. In general, among the specified models, the CBDW-3B approximation is better suited for explaining the features exhibited by the measured cross-sections.
 | Fig. 2. Angular distribution of the single-electron capture differential cross sections for incident energy of 150 keV/amu. |
The results for the prior and post differential single electron capture cross sections in fast 3He+ – 4He collisions at 300 keV/amu are displayed in Fig. 3. The experimental data given by Schö ffler et al.[20] and the theoretical data from the four-body CDW-BIS[20] and three-body CBDW theories[6] are also depicted in this figure. The prior and post graphs, which coincide with each other at angles beyond the dark angle, are not in good agreement with the experimental measurements in this angular region. Also, a significant discrepancy can be seen between the prior and the post curves at extreme forward scattering angles. In the CBDW-3B computations, neglecting the dynamic electron correlation causes some deflection from the experimental results in this angular region. At the angles around the zero scattering angle, the results of the post CBDW-4B theory are in excellent agreement with the experimental findings. A complex structure is observed in CDW-BIS around the dark angle, while such a structure is absent both in experimental and other theoretical results. Except for a narrow cone around the zero scattering angle, the CBDW-3B theory gives a better description of the collision dynamics.
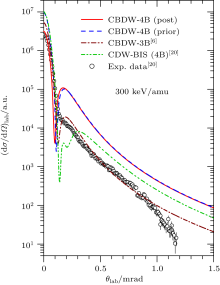 | Fig. 3. Angular distribution of the single-electron capture differential cross sections for incident energy of 300 keV/amu. |
Differential cross sections as a function of the laboratory scattering angle for the same reaction at incident energy 630 keV/amu are depicted in Fig. 4. At small angles, our post results are much closer to the experimental distribution than those of the other theories. For scattering angles below the dark angle, these results are in reasonable accordance with the experiment. However, for angles above the dark angle, both the post and the prior results coincide with each other and are considerably larger than the experimental results as well as other theoretical results. Similar to the previous case, the four-body CDW-BIS method shows a complex structure in an angular region around the scattering angle of 0.2 mrad.
 | Fig. 4. Angular distribution of the single-electron capture differential cross sections for incident energy of 630 keV/amu. |
As is seen, for larger scattering angles, our results are deflect relative to the experimental data, possibly due to the fact that the specified collision is a five-body collision, while we assume that one electron is frozen to the projectile nucleus, thus neglecting the effect of its interaction with the active electron of the target. Another reason for the deflection from the experimental data may be related to the fact that the effect of the second and higher order terms in the present formulation increases when the impact energy increases and the first-order approximation is not sufficient for the presentation of all the patterns exhibited in the experimental data.
Another issue that we wish to examine is the sensitivity of the present formalism to the static correlation of the two electrons in the helium target. Toward this end, we compare the results obtained from the two different wave functions describing the initial bound state of these electrons: the single-zeta and the highly correlated multi-parameter Byron– Joachain[35] wave functions. The latter wave function is given by

with A = 2.60505, B = 2.08144, ζ = 1.41, and ζ ′ = 2.61. For all the above discussed impact energies, a comparison of the results shows that a sensible discrepancy does not exist between the differential cross sections computed by means of these different wave functions. In other words, the present formalism is not so sensitive to the static correlation. For example, figure 5 compares the prior and the post differential cross sections obtained by means of the single-zeta and the correlated Byron– Joachain wave functions for an impact energy of 60 keV/amu. As is seen, the difference between the corresponding results is marginal. However, the post results are in better agreement with the experiment. The fact that the ground-state correlation has little effect on the capture cross sections is also supported by the other studies of the different charge transfer processes (see for example Refs. [8] and [14]).
An overview of Figs. 1– 5 shows that the present theory is not suitable to explain the collision dynamics. Because it predicts an unphysical dip in the angular distribution of the differential cross sections. Also the predicted results are significantly larger than their corresponding experimental values at larger scattering angles. A similar feature has been discussed for positronium formation from multi-electron targets in Ref. [36]. However, the present results show that, in a small angular region around the zero scattering angle, the inclusion of the inter-electron potential responsible for the dynamic electron correlation in the CBDW-4B amplitude would reduce the deflection of the results from the experiments. Also, the static correlation does not affect the theoretical results considerably.
It is a difficult task to explain why the present CBDW-4B results, contrary to what one would expect, do not improve over those CBDW-3B calculations. This is an issue that warrants further study. However, we can refer to a number of possible causes for the discrepancy between these models. (i) The initial bound-state wave functions for the two models are different. The four-body model uses a two-electron wave function with correlation, while the three-body model uses a one-electron wave function. (ii) In the three-body model, the residual helium ion in the final state is considered as a particle without internal structure, while in the four-body model, it is considered as a bound subsystem which is described by a hydrogen-like wave function. (iii) Both the initial and the final perturbation potentials are different for the two models. (iv) In the CBDW-4B model, only the final state is distorted by the residual Coulomb interaction, while in the three-body model, both the initial and the final states are distorted by the corresponding Coulomb residuals. It seems that in the three-body formalism including the initial and final Coulomb distortions and considering an effective nuclear charge for the target ion gives a better description of the average influence of the static and dynamic correlations on the collision process than what is done in the four-body formalism. Another issue which should be examined in further study is whether including the second-order transition amplitudes in the computations improves the accuracy of the four-body results relative to those of the three-body approach. Inclusion of the second-order calculations in the CBDW formalisms and comparison of the obtained results with the experiment allow for the accuracy of the three- and four-body approaches to be assessed. Also it is helpful to give insight into which physical aspects of the considered collision process are most important in the accuracy of the model.
The CBDW-4B calculated post integral cross sections for single charge transfer in 4He+ – 4He collisions, obtained with the complete perturbation potential for energies between 60 keV/amu to 5000 keV/amu, are depicted in Fig. 6. These results are compared with a number of available experimental data, [24– 29] and also with the corresponding results obtained from the four-body first Born (CB1-4B), [15, 16] the four-body continuum distorted wave, (CDW-4B)[15] and CBDW-3B methods.[6] It is assumed that the projectile passive electron remains in its atomic ground state during the collision. The computation of the total cross sections is performed only for the final ground state (for 1s → 1s transition). The obtained results are multiplied additionally by a factor of 1.404 in order to include a contribution from the excited states according to the well-known n− 3 Oppenheimer scaling law. Contrary to the differential case, the integral cross sections are in excellent agreement with the experiment. They are also a little larger than, but compatible with, the CBDW-3B results.[6] A comparison of these results with those of the CB1-4B and CDW-4B shows that the CBDW-4B model is in better agreement with the experiment at smaller scattering energies. The difference between the results obtained from different four-body theories becomes ignorable as the impact energy increases.
An analysis of the prior and the post forms of the transition amplitude in the four-body Coulomb– Born distorted-wave approximation with correct boundary conditions (CBDW-4B) has been carried out for single electron transfer in the collision of the fast singly positive helium ions with helium atoms. An important criterion for establishing the usefulness of the given theoretical model has been provided by comparing the results with the experimental results. In spite of the fact that a three-body version of the approximation gives good estimates of the differential and integral cross-sections for different ion– atom collision systems, its four-body version is not so successful in explaining the features exhibited in the experiments for the differential cross sections. Especially for the prediction of an unphysical sharp dip in the angular distribution of the differential cross sections and also for large deflections of the results from the experiment at scattering angles beyond the dark angle, it becomes difficult to draw a definite conclusion about the extent of the validity of the present model. A similar situation was observed for the other four-body theory (CDW-BIS) discussed through the previous section. The only advantage of the present theory is that it improves the theoretical results for extreme forward scattering angles by including the interaction potential responsible for the dynamic correlation in the post form of the transition amplitude. Also, it is shown that the CBDW-4B differential and subsequently integral cross-sections are not so sensitive to the choice of the initial bound-state wave function. Accordingly, the static correlation does not play a significant role in addressing the various aspects of the cross sections. In general, the prior– post discrepancy is marginal for scattering angles beyond the dark angle, and for smaller angles, the post cross sections indicate better agreement with the experimental data. Also, as the impact energy increases, the discrepancy between the prior and the post cross sections decreases. Contrary to the fact that the present four-body approximation fails to give a good description of experiments for the differential cross sections especially at larger scattering angles, it gives results in good agreement with the experimental total cross sections. The present results for the total cross section are more satisfactory than those of the CB1-4B and CDW-4B theories, particularly for lower incident energies, and are also compatible with the results of the CBDW-3B approach across all of the considered energy range.
One of the authors, HG, wishes to acknowledge the office of graduate studies at the University of Isfahan for their support and research facilities.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|





