Cite this Article
Zhang Pei-Pei, Zhong Zhen-Xiang, Yan Zong-Chao, Shi Ting-Yun. Precision calculation of fine structure in helium and Li+* . Chinese Physics B, 2015, 24(3): 033101  
Permissions
Precision calculation of fine structure in helium and Li+*
Zhang Pei-Peia),b), Zhong Zhen-Xianga)†, Yan Zong-Chaoa),c), Shi Ting-Yuna)
Division of Theoretical and Interdisciplinary Research, State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, and Center for Cold Atom Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China
University of Chinese Academy of Sciences, Beijing 100049, China
Department of Physics, University of New Brunswick, Fredericton, New Brunswick E3B 5A3, Canada

†Corresponding author. E-mail: zxzhong@wipm.ac.cn

*Project supported by the National Basic Research Program of China (Grant No. 2010CB832803).

Abstract

The fine structure constant α can be extracted from high-precision spectroscopy of the 23P J fine structure splittings in helium and light helium-like ions. In this work, the 23P J fine structure splittings of helium and Li+ ion are calculated, including relativistic and QED corrections of order m α4, m α4( m/ M), m α5, m α5( m/ M), and Douglas–Kroll operators of m α6 and m α6( m/ M), which provide an independent verification for the previous calculations performed by Drake [ Can. J. Phys.80 1195 (2002)] and by Pachucki and Yerokhin [ Phys. Rev. A79 062516 (2009); Phys. Rev. Lett.104 070403 (2010); Can. J. Phys.89 1139 (2011)]. The results of the three groups agree with each other.

Keyword: 31.15.ac; 37.10.De; 31.15.ap; 31.15.bw; fine structure; helium; Li+ ion; QED theory
1. Introduction

The fine structure of the 23PJ states of helium and light helium-like ions has attracted theoretical and experimental interest for several decades. Due to the fact that the fine structure splitting in a light atomic system is an intrinsically relativistic effect and is proportional to α 2 in the lowest order, study on the fine structure holds a potential for testing bound-state QED and for an accurate determination of the fine structure constant α . Many theoretical studies have concentrated on the fine structure of helium and helium-like ions since the work of Schwartz.[1] Early studies aiming at order mα 6 (or α 4 Ry) corrections can be found in Refs.  [2]– [5], which corresponds to the determination of α at a level of a few parts per million (ppm). Subsequently, Yan and Drake improved the calculations on the fine structure splittings of helium and helium-like ions (Z ≤ 10) by including all terms up to mα 6, at the level of 3 parts per billion (ppb).[6– 8]

The calculations of higher-order corrections met serious difficulties. For the first time, Zhang et al.[9– 12] derived the order mα 7 relativistic Bethe logarithm correction. Although the computational uncertainty was much less than 1  kHz, there was an unexplained discrepancy between theoretical[13, 14] and experimental values.[15– 18] Pachucki and Serpirstein[19, 20] pointed out several computational mistakes and inconsistencies in Zhang’ s calculation. In 2006, the entire mα 7 order corrections were derived by Pachucki.[21] Nonetheless, the theoretical calculations turned out to be not only in disagreement with each other but also in disagreement with experiments.[22, 23] Pachucki and Yerokhin[24] eliminated this disagreement by reevaluating the relativistic Bethe logarithm term. As a result, they determined the value of α with an accuracy of 31  ppb, in which the theoretical and experimental uncertainties were respectively 39  ppb and 16  ppb.[15– 18, 22, 23, 25] Later, the experimental uncertainty was reduced to 5  ppb by Smiciklas and Shiner, [26] where the uncalculated higher-order terms of order mα 8 hindered α from a further improvement in precision.

Besides the helium atom, the fine structure of the Li+ ion can be used for the α determination as well, in which the theoretical uncertainty is about 3 × 10− 7.[24] The experimental measurements of Li+ have a precision of 4 × 10− 6.[27– 30]

There are some other theoretical studies for energy levels of helium and helium-like ions based on different approaches. Qing et al. calculated the fine structure of helium and helium-like ions with the multi-configuration Dirac– Fock method, including the Breit interaction and QED corrections. Their results agree with experiments within about 1%.[31] Duan et al. calculated the nonrelativistic ground-state energy of helium using Hylleraas coordinates, as well as the relativistic and radiative corrections.[32]

In this paper, we intend to calculate relativistic corrections of order mα 4, mα 4(m/M), mα 5, mα 5(m/M), and Douglas– Kroll operators of mα 6 and mα 6(m/M) corrections for the fine structure splittings of helium and Li+ , with a purpose of providing a third-party independent verification of previous theoretical work, and further improving computational accuracy for these operators, which is necessary for studying mα 8 corrections.

2. Methodology and energies
2.1. Variational wavefunction

After removing the center of mass motion, the three-body Hamiltonian can be expressed as (in atomic units of ħ = e = m = 1)

where M is the nuclear mass, r1 and r2 represent the position vectors of the two electrons respectively, relative to the nucleus situated at the origin, V = − Z/r1 − Z/r2 + 1/r12 is the Coulomb interaction, and r12 = r1 − r2. The eigenvalue problems for helium and Li+ are solved variationally by using the following generalized Hylleraas basis set:

In the above, is the vector coupled product of spherical harmonics for the two electrons to form a common eigenvector of L2, Lz, and Π with the corresponding eigenvalues of L(L + 1), M, and (− 1)l1+ l2, respectively. Here L is the total orbital angular momentum quantum number with its z-component being M, and l1 and l2 are orbital angular momentum quantum numbers for electrons 1 and 2 respectively.

Instead of generating nonlinear parameters in a quasirandom manner used by Korobov[33] and Pachucki, [24] we optimized the nonlinear parameters (α , β , γ ) using Newton’ s method. For the case of infinite nuclear mass, our results for the nonrelativistic energies of 23P states of helium and Li+ ion are respectively

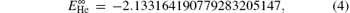
which are accurate enough for our calculations of relativistic and radiative corrections.

2.2. Contributions to the fine structure splittings

According to bound-state quantum electrodynamic (QED) theory, atomic energy levels can be expressed in powers of the fine structure constant α ,

The term is of the order mα nε n, where m is the electron mass and ε n is an expectation value of a collection of operators or an effective Hamiltonian of this order that needs to be evaluated in theory. The leading contribution to fine structure splittings is the relativistic corrections of order mα 4, with the corresponding operators being called Breit (or Breit– Pauli) operators.[34] Since the spin-independent part contributes equally to all fine structure levels, only the spin-dependent part is needed for calculating the fine structure splittings

where HZso is the spin– orbit interaction with the nucleus, Heso is the spin– orbit interaction between two electrons, and Hess is the spin– spin interaction between two electrons. In addition, there are anomalous magnetic moment corrections to Breit operators, which is H(5) of mα 5 order correction

The factor δ SS′ means that Heso does not contribute to singlet-triplet mixing terms.

The order mα 6 corrections to the fine structure splittings contain two parts. The first part is the second-order perturbation corrections deduced by the Breit– Pauli operators, [34] denoted as corrections. The validity of this second-order perturbation approach was justified by Douglas and Kroll.[2] The second part is the 15 spin-dependent operators HDK, denoted as corrections. The Douglas– Kroll operators were first derived by Douglas and Kroll in the frame of the Bethe– Salpeter equation; [2] then these operators were rederived by Pachucki using an effective field method.[35] The Douglas– Kroll operators arise from the Feynman diagrams involving the exchange of one, two, and three photons, as well as radiative corrections to the electron magnetic moment. The matrix elements were first calculated by Daley and coworkers.[36] Then higher precision values for these operators were obtained by Yan and Drake[7] and by Pachucki.[19] Thus, the total expression for the mα 6 order corrections is

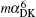
where H(4) contains both the spin-dependent and spin-independent parts of Breit– Pauli operators. The expressions of the Douglas– Kroll operators can be written as follows:

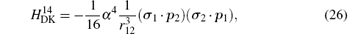
For the sake of convenience, we first consider the case of infinite nuclear mass. We then consider finite nuclear mass corrections. The finite nuclear mass corrections of each order can be divided according to the effects of mass polarization and nuclear recoil. The mass polarization effect can be accounted for to all orders by reevaluating the expectation values of all operators using a wavefunction with the mass polarization term ∇ r1 · ∇ r2/M included explicitly in the Hamiltonian and taking difference with the infinite nuclear mass results. The terms and in Tables  1 and 2 represent the mass polarization effects to the Douglas– Kroll operators for helium and Li+ , respectively. It is convenient to denote those terms as . On the other hand, the mass polarization effects to the second-order perturbation terms are labeled as .

Table 1. Contributions of the Douglas– Kroll operators to the fine structure intervals in the 23PJ state of helium (in units of 10− 6R∞ cα 4 = 9.329027  MHz).
Table 2. Contributions of the Douglas– Kroll operators to the fine structure intervals in the 23PJ state of Li+ ion (in units of 10− 6R∞ cα 4 = 9.329027  MHz).

The other part of the finite nuclear mass corrections are recoil terms which disappear in the case of infinite nuclear mass. The mα 4(m/M) and mα 5(m/M) order recoil corrections are

Since the HZso appears in the mα 4 order relativistic corrections, Hrec is the only term needed to be considered in this part. The mα 6 order recoil corrections, labeled as 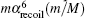, are much more complicated. It was first discussed by Zhang[11] using Bethe– Salpeter formalism, followed by a reconsideration by Pachucki and Sapirstein[20] using effective Hamiltonian approach that yields a sign difference in v6 (see Eq.  (36)). Eventually the results of turned out to be consistent after Drake revised the sign.[14] The order recoil corrections are listed below.

Finally, the corrections of orders , , and mα 7 are not considered in this work.

3. Calculation and numerical results

The fine structure splittings ν 01 and ν 12 are defined by

Convergence studies for the operators HZso, Heso, Hess, and Hrec are presented in Tables  3 and 4 for the 2 3PJ states of helium and Li+ , respectively. One can see that numerical accuracy of these operators can reach a precision of 12– 14 significant digits. A comparison of our results with previous work by Yan[8] shows some discrepancies. Yan used about 800 terms of the basis set, while we used more than 4000, which may explain the discrepancies.

Table 3. Convergence study of the reduced matrix elements of the spin-dependent Breit operators for the helium 2 3PJ state (in 10− 2 Hartree energy).
Tabel 4. Convergence study of the reduced matrix elements of the spin-dependent Breit operators for the Li+ ion 23PJ state (in 10− 2 Hartree energy).

Numerical results of the Douglas– Kroll operators of mα 6 order corrections are listed in Tables  1 and 2 for the fine structure intervals of 2 3PJ of helium and Li+ , respectively. A term-by-term comparison with previous work by Pachuchi[19] is presented as well. The total uncertainties of the Douglas– Kroll operators to the fine structure intervals are reduced to a level of Hz or even sub-Hz, which is beyond the need for the fine structure constant determination. We do not calculate the second-order perturbation corrections of Breit– Pauli operators; instead, we used Pachucki’ s and Drake’ s results that are in good accordance. The numerical results of the finite mass recoil operators, of order, are presented in Tables  5 and 6 for the fine structure intervals of helium and Li+ , respectively.

Table 5. Contributions of finite nuclear mass recoil operators for the order corrections to the fine structure intervals in the 2 3PJ state of helium atom (in kHz).
Table 6. Contributions of finite nuclear mass recoil operators for the order corrections to the fine structure intervals in the 2 3PJ state of Li+ ion (in kHz).

The numerical results of contributions of all corrections to the fine structure intervals are listed in Tables  7, 8, and 9 for the 2 3PJ states of helium and Li+ , respectively. A detailed term-by-term comparison with previous work is presented as well. Our values of mα 4, mα 4(m/M), mα 5, and mα 5(m/M) order corrections agree with previous calculations[14, 24, 38] perfectly due to the high-precision values for HZso, Heso, Hess, and Hrec in Tables  3 and 4. The uncertainties of these orders are entirely due to the fundamental physical constants. For the mα 6 order and mα 6(m/M) order corrections, we calculate the Douglas– Kroll operators (see Tables  1, 2, 5, and 6). The uncertainties of and order contributions have been reduced by two orders of magnitude, as shown in Table  7.

Table 7. Comparison of the contributions to the fine structure intervals of helium in 2 3PJ (in MHz).
Table 8. The final results of the fine structure intervals for helium in 2 3PJ (in MHz).
Table 9. Comparison of the contributions to the fine structure intervals of Li+ in 2 3PJ (in MHz).

We also provide a comparison of the total intervals with other theories and experiments. In Tables  8 and 9, we take values of uncalculated terms from other theories in order to sum up all contributions. For the helium atom, one can see that our total intervals agree with the values from Ref.  [38], but differ from Drake’ s calculation.[14] This is due to the mistakes of the derivations and calculations of mα 7 order corrections in Refs.  [9]– [12]. It should be pointed out that the total intervals have slight discrepancies between our values and the values of Pachucki and Yerokin.[38] This is due to the shift of about 0.5  kHz for the order corrections in both ν 01 and ν 12 (see Table  7). For the Li+ ion, we reproduce the results of Pachucki and Yerokhin.[24] The total uncertainties of the intervals come from other higher-order corrections not calculated in this work. The largest uncertainty in the total intervals for both helium and Li+ is due entirely to the unknown mα 8 order corrections.

4. Conclusion

In conclusion, we have performed an independent calculation of the fine structure intervals for the 2 3PJ states of helium and Li+ including mα 4, mα 4(m/M), mα 5, mα 5(m/M), , , and order corrections. Our results agree with previous calculations at a sub-kHz level for these corrections. The numerical uncertainties of our results are negligible compared to the present experimental uncertainty. The current values of the order corrections have a shift of about 0.5  kHz for both ν 01 and ν 12 (see Tables  7 and 9), which was analyzed by Pachucki.[37] He pointed out that this discrepancy exceeds the present experimental precision of Ref.  [26] and should be checked theoretically. The uncertainties of order and order corrections exceed the experimental uncertainty, and the non-logarithmic parts of are only calculated by Pachucki. As a result, further verification is also needed. The most accurate value for α − 1 determined from the helium fine structure is 137.035 999 55(368), [39] in combination with the experimental results of Smiciklas and Shiner[26] and the theoretical result of Pachucki and Yerokhin, [24] where the uncertainty is mainly caused by uncalculated higher-order terms. The uncalculated contribution of order mα 8 is estimated to be ± 1.7  kHz, resulting in a relative uncertainty of 2.7 × 10− 8 for α .[40] A complete calculation of order mα 8 terms is still a challenging task.

Acknowledgment

Yan Z C is supported by the Natural Sciences and Engineering Research Council of Canada, the computing facilities of ACEnet and SHARCnet, and by the CAS/SAFEA International Partnership Program for Creative Research Teams.

Reference
1 Schwartz C 1964 Phys. Rev. 134 A1181 DOI:10.1103/PhysRev.134.A1181 [Cited within:1] [JCR: 6.583]
2 Douglas M H and Kroll N M 1974 Ann. Phys. 82 89 DOI:10.1016/0003-4916(74)90333-9 [Cited within:3] [JCR: 0.25]
3 Hambro L 1972 Phys. Rev. A 5 2027 DOI:10.1103/PhysRevA.5.2027 [Cited within:1] [JCR: 3.042]
4 Hambro L 1973 Phys. Rev. A 7 479 DOI:10.1103/PhysRevA.7.479 [Cited within:1] [JCR: 3.042]
5 Lewis M L and Serafino P H 1978 Phys. Rev. A 18 867 DOI:10.1103/PhysRevA.18.867 [Cited within:1] [JCR: 3.042]
6 Yan Z C and Drake G W F 1994 Can. J. Phys. 72 822 DOI:10.1139/p94-109 [Cited within:1] [JCR: 0.902]
7 Yan Z C and Drake G W F 1995 Phys. Rev. Lett. 74 4791 DOI:10.1103/PhysRevLett.74.4791 [Cited within:1] [JCR: 7.943]
8 Yan Z C 1994 Order α6 mc2 Contributions to the Fine Structure Splittings of Helium and Helium-like Ions(Ph. D. Thesis) Windsor University of Windsor [Cited within:2]
9 Zhang T 1996 Phys. Rev. A 53 3896 DOI:10.1103/PhysRevA.53.3896 [Cited within:2] [JCR: 3.042]
10 Zhang T 1996 Phys. Rev. A 54 1252 DOI:10.1103/PhysRevA.54.1252 [Cited within:1] [JCR: 3.042]
11 Zhang T and Drake G W F 1996 Phys. Rev. A 54 4882 DOI:10.1103/PhysRevA.54.4882 [Cited within:1] [JCR: 3.042]
12 Zhang T, Yan Z C and Drake G W F 1996 Phys. Rev. Lett. 77 1715 DOI:10.1103/PhysRevLett.77.1715 [Cited within:2] [JCR: 7.943]
13 Pachucki K and Sapirstein J 2000 J. Phys. B: At. Mol. Opt. Phys. 33 5297 DOI:10.1088/0953-4075/33/23/303 [Cited within:1] [JCR: 2.031]
14 Drake G W F 2002 Can. J. Phys. 80 1195 DOI:10.1139/p02-111 [Cited within:4] [JCR: 0.902]
15 Minardi F, Bianchini G, Pastor P C, Giusfredi G, Pavone F S and Inguscio M 1999 Phys. Rev. Lett. 82 1112 DOI:10.1103/PhysRevLett.82.1112 [Cited within:2] [JCR: 7.943]
16 Castillega J, Livingston D and Hessels E A 2000 Phys. Rev. Lett. 84 4321 DOI:10.1103/PhysRevLett.84.4321 [Cited within:1] [JCR: 7.943]
17 Storry C H, George M C and Hessels E A 2000 Phys. Rev. Lett. 84 3274 DOI:10.1103/PhysRevLett.84.3274 [Cited within:1] [JCR: 7.943]
18 George M C, Lombardi L D and Hessels E A 2001 Phys. Rev. Lett. 87 173002 DOI:10.1103/PhysRevLett.87.173002 [Cited within:2] [JCR: 7.943]
19 Pachucki K and Sapirstein J 2002 J. Phys. B: At. Mol. Opt. Phys. 35 1783 DOI:10.1088/0953-4075/35/7/314 [Cited within:3] [JCR: 2.031]
20 Pachucki K and Sapirstein J 2003 J. Phys. B: At. Mol. Opt. Phys. 36 803 DOI:10.1088/0953-4075/36/5/301 [Cited within:2] [JCR: 2.031]
21 Pachucki K 2006 Phys. Rev. Lett. 97 013002 DOI:10.1103/PhysRevLett.97.013002 [Cited within:1] [JCR: 7.943]
22 Zelevinsky T, Farkas D and Gabrielse G 2005 Phys. Rev. Lett. 95 203001 DOI:10.1103/PhysRevLett.95.203001 [Cited within:2] [JCR: 7.943]
23 Giusfredi G, Cancio Pastor P, De Natale P, Mazzotti D, de Mauro C, Fallani L, Hagel G, Krachmalnicoff V and Inguscio M 2005 Can. J. Phys. 83 301 DOI:10.1139/p04-075 [Cited within:2] [JCR: 0.902]
24 Pachucki K and Yerokhin V A 2010 Phys. Rev. Lett. 104 070403 DOI:10.1103/PhysRevLett.104.070403 [Cited within:6] [JCR: 7.943]
25 Borbely J S, George M C, Lombardi L D, Weel M, Fitzakerley D W and Hessels E A 2009 Phys. Rev. A 79 060503(R) DOI:10.1103/PhysRevA.79.060503 [Cited within:1] [JCR: 3.042]
26 Smiciklas M and Shiner D 2010 Phys. Rev. Lett. 105 123001 DOI:10.1103/PhysRevLett.105.123001 [Cited within:3] [JCR: 7.943]
27 Rong H, Grafström S, Kowalski J, zu Putlitz G, Jastrezebski W and Neumann R 1993 Z. Phys. D 25 337 DOI:10.1007/BF01437300 [Cited within:1]
28 Riis E, Sinclair A G, Poulsen O, Drake G W F, Rowley W R C and Levick A P 1994 Phys. Rev. A 49 207 DOI:10.1103/PhysRevA.49.207 [Cited within:1] [JCR: 3.042]
29 Clarke J J and van Wijngaarden W A 2003 Phys. Rev. A 67 012506 DOI:10.1103/PhysRevA.67.012506 [Cited within:1] [JCR: 3.042]
30 van Wijngaarden W A and Noble G A 2008 Lect. Notes Phys. 745 111 DOI:10.1007/978-3-540-75479-4 [Cited within:1]
31 Qing B, Chen S H, Gao X and Li J M 2008 Chin. Phys. Lett. 25 2448 http://118.145.16.217/magsci/article/article?id=17360661 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
32 Duan Y S, Liu Y X and Zhang L J 2004 Chin. Phys. Lett. 21 1714 http://118.145.16.217/magsci/article/article?id=17356911 [Cited within:1] [JCR: 0.811] [CJCR: 0.4541]
33 Korobov V I 2000 Phys. Rev. A 61 064503 DOI:10.1103/PhysRevA.61.064503 [Cited within:1] [JCR: 3.042]
34 Bethe H A and Salpeter E E 1957 Quantum Mechanics of One- and Two-electron Atoms Berlin Springer-Verlag OHG 181 [Cited within:2]
35 Pachucki K 1999 J. Phys. B 32 137 DOI:10.1088/0953-4075/32/1/014 [Cited within:1] [JCR: 3.607]
36 Daley J, Douglas M, Hambro L and Kroll N M 1972 Phys. Rev. Lett. 29 12 DOI:10.1103/PhysRevLett.29.12 [Cited within:1] [JCR: 7.943]
37 Pachucki K and Yerokhin V A 2009 Phys. Rev. A 79 062516 DOI:10.1103/PhysRevA.79.062516 [Cited within:1] [JCR: 3.042]
38 Pachucki K and Yerokhin V A 2011 Can. J. Phys. 89 1139 [Cited within:3] [JCR: 0.902]
39 Pachucki K and Yerokhin V A 2011 J. Phys. Conf. Ser. 264 012007 DOI:10.1088/1742-6596/264/1/012007 [Cited within:1]
40 Mohr P J, Taylor B N and Newell D B 2012 Rev. Mod. Phys. 84 1527 DOI:10.1103/RevModPhys.84.1527 [Cited within:1] [JCR: 44.982]