†Corresponding author. E-mail: cquwzh@163.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 51207173 and 51277192).
This paper presents a modified sliding mode control for fractional-order chaotic economical systems with parameter uncertainty and external disturbance. By constructing the suitable sliding mode surface with fractional-order integral, the effective sliding mode controller is designed to realize the asymptotical stability of fractional-order chaotic economical systems. Comparing with the existing results, the main results in this paper are more practical and rigorous. Simulation results show the effectiveness and feasibility of the proposed sliding mode control method.
Fractional calculus has a history of more than 300 years. Although it has a long history, the applications of fractional calculus to physics and engineering are only a recent focus of interest.[1, 2] Nowadays, it has been found that many systems in interdisciplinary fields, such as viscoelastic materials, [3] electrode-electrolyte polarization, [4] thermoelectric systems, [5] dielectric polarization, [6] etc., can be elegantly described by fractional differential derivatives.
In the past decade, econophysics have become an alternative scientific methodology to understand the highly complex dynamics of real financial or economical systems. These economists present a model to explain the central features of economic data (such as irregular growth, structural changes, erratic macroeconomic fluctuations, and so on). The model is often affected by exogenous shock variables and displays irregular and random behavior. Typical random shocks coming from external influence include weather variables, political events, and other human factors. It is worth mentioning that chaos can give a reasonable explanation of the above mentioned complexity.[7] Nowadays, the importance of chaos in economics has increased tremendously and many chaotic models have been used to study the complex economical systems.[8– 11]
On the other hand, research interest has been growing in fractional calculus not only from physicists and engineers but also from researchers in life science and economics. In fact, financial variables possessing long memories make fractional models more appropriate for dynamic behaviors in finance. The magnitude of the financial variables (such as foreign exchange rates, gross domestic product, interest rates, production and stock market prices) can have a long memory. Research on fractional-order economical system has a wider range of applications. Chen[7] studied nonlinear dynamics and chaos in a fractional-order financial system. Wang et al.[12] proposed a delayed fractional-order financial system and discussed its complex dynamical behaviors by numerical simulations. Abd-Elouahab et al.[13] extended the nonlinear feedback control in ODE systems to fractional-order financial systems in order to eliminate the chaotic behavior. Wang et al.[14] addressed the synchronization problem of chaotic fractional-order economical system via active control. Chen et al.[15] studied the control and synchronization of fractional-order financial systems by the Routh– Hurwitz stability condition and linear control method.
Moreover, the control and synchronization of fractional-order dynamical systems has attracted a great deal of interest.[16– 22] The most common control methods include the active control method, [23– 25] sliding mode control method, [26– 29] adaptive control method, [30– 32] observer-based control method, [33– 35] impulsive control method, [36– 38] etc. Among these methods, sliding mode control (SMC) is an efficient method to deal with the robust control scheme. The main feature of SMC is to switch the control law to force the states of the system from the initial states onto some predefined sliding mode surface. The system on the surface has desired performance, such as stability, disturbance rejection capability, and tracking ability.
Recently, sliding mode control schemes for the fractional-order economical system are becoming a matter of concern for more and more researchers.[39, 40] In Ref. [39], the sliding mode control just includes one single feedback controller, which is simple and easy to implement. However, the dynamics analysis of the designed sliding surface is not given, which cannot ensure desired performance. In Ref. [40], the designed sliding surface satisfies exponential reaching law, but the full state feedback controller is necessary. Moreover, the controlled system is a fractional-order linear system with bound input, and its stability does not conform to the stability theorem for fractional-order linear system. Motivated by the aforementioned discussion, in this paper we address the modified sliding mode control scheme for a class of fractional-order chaotic economical systems. Compared with Refs. [39] and [40], the proposed sliding mode surface meets the existence condition with desired dynamics, and the designed single controller is easy to implement to realize the robust control of the fractional-order economical system.
The rest of this paper is organized as follows. In Section 2, the problem formulation for the sliding mode control is provided. Main results for the sliding mode control of fractional-order chaotic economical system with or without parameter uncertainty and external disturbance are derived in Section 3. In Section 4, two illustrative examples for fractional-order economical system are presented to demonstrate the effectiveness and feasibility of the proposed method. Finally, concluding remarks are given in Section 5.
In Refs. [10] and [11], a dynamic model of finance, composed of three first-order differential equations, is presented. The model describes the time-variation of three state variables, i.e., the interest x, the investment demand y, and the price index z, which can be expressed by
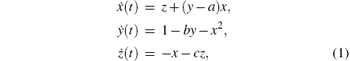
where a> 0 is the saving amount, b> 0 is the cost per investment, and c> 0 is the elasticity of demand of the commercial markets. Recently, Chen generalized system (1) to a fractional-order version[7]
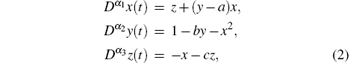
where Dα (· ) denotes the Caputo fractional derivative of α ∈ (0, 1), defined as follows:[1]
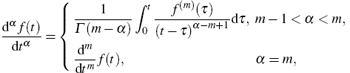
where m is the first integer larger than α , and Γ (α ) is the Euler gamma function given by
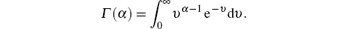
By using the linear fractional-order stability theorem (system Dα X= AX is asymptotical stable if |arg(eig(A))|> α π /2 holds), it is easy to see that if y= 0, the following two-dimensional subsystem of system (2):

is asymptotically stable about the origin x= 0 and z= 0 for all x and z (where 
In the following section, we will propose the novel single state sliding mode controller to realize the finite time stability of state y, which is added to the second state equation,

Remark 1 The controlled system (4) just contains one single controller u(t), which is more energy-efficient than full state feedback controller. On the other hand, the controller u(t) is added into the second equation (to realize the state y(t)= 0 in finite time) rather than the first and third ones in system (4). This is due to the fact that the linear subsystem (3) is asymptotically stable according to the linear fractional-order stability theorem. If the controller is added into the first or third one to make x(t)= 0 or z(t)= 0, then the subsystems
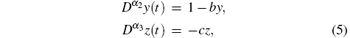
and
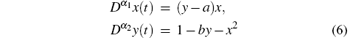
are not linear, and cannot satisfy the stability condition for linear fractional-order system.
The main idea of sliding mode control is to design a discontinuous control to force the system state trajectories to some predefined sliding mode surface, which is composed of two steps: 1) constructing a sliding mode surface that has desired properties; 2) developing a switch control law to make the trajectories reach the surface and stay on it evermore.
We choose the following nonsingular fractional-order sliding mode surface as:

where sign(· ) is the sign function, k> 0, and γ ∈ (0, 1) are constants.
Once the system trajectory reaches the sliding surface (7), it yields the following equations:
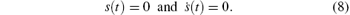
From Eqs. (7) and (8), the dynamics of sliding mode can be achieved as follows:
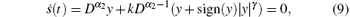
it further yields
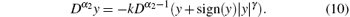
Before we give the main results, the fractional-order Lyapunov stability theorem can be stated as follows.
Lemma 1[41] Let x= 0 be an equilibrium point for the nonautonomous fractional-order system,

where f(t, x) satisfies the Lipschitz condition with Lipschitz constant l> 0 and α ∈ (0, 1). Assume that there exists a Lyapunov function V(t, x) satisfying
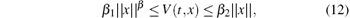

where β 1, β 2, β 3, and β are positive constants. Then the equilibrium point of the system (11) is Miattag– Leffler (asymptotic) stable.
In the following theorem, the finite-time stability of the sliding surface (7) is proved.
Theorem 1 The sliding mode dynamic (10) is asymptotic stable and its trajectory converges to the equilibrium y= 0 in a finite time.
Proof Considering the following Lyapunov function:
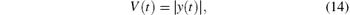
and its derivative along the trajectory of system (10) is
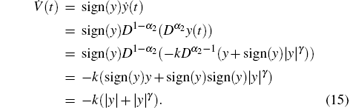
Since |y| and |y|γ are positive, it yields that
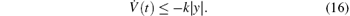
From Lemma 1, the Lyapunov function V(t) satisfies condition (12) (if let β 1= 0.5, β 2= 2, and β = 1) and condition (13) (with β 3= k> 0), thus the system state y(t) will converge to zero asymptotically. In the following, the finite-time convergence of y(t) will be further investigated.
From Eq. (15), we have

It is obvious that
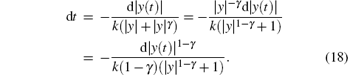
By taking the integral of both sides of Eq. (18) from t1 to t2 (t1 is the reaching time for state y(t) to the sliding surface s(t) and t2 is the convergence time for y(t) to zero), and considering y(t2)= 0, thus we have

Therefore, the state trajectory y(t) can converge to zero in finite time
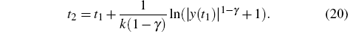
We complete the proof.
After constructing a fractional-order sliding mode surface, the second step is to design a nonlinear feedback controller u(t) to force the error state y(t) to reach the sliding surface and stay on it evermore. In what follows, we propose the suitable controller to ensure the existence of the sliding motion.
Theorem 2 If system (2) is controlled with the following controller:
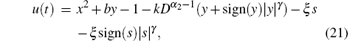
where k> 0, ξ > 0, and γ ∈ (0, 1) are constants, then the system state y(t) will converge to the sliding surface s(t)= 0 in finite time.
Proof Selecting a Lyapunov function in the form of V(t)= |s(t)| and the time derivative of V(t) is obtained as follows:

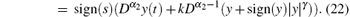
From systems (4), (21), and (22), we have
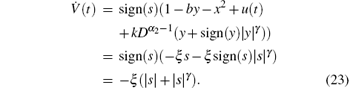
Obviously, the system state trajectories will converge to the sliding surface s(t)= 0 asymptotically. Similar to the proof of Theorem 1, we can also obtain the results that the sliding motion occurs in finite time. Referring to Eqs. (17)– (19), the reaching time t1 can be derived as
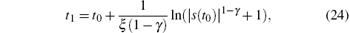
where t0 is the initial time. The detailed proof is similar to that of Theorem 1, which is omitted here. We complete the proof.
Remark 2 From Theorems 1 and 2, we can obtain that the state trajectories of system (2) will first converge to s(t)= 0 in finite time t1, and then the state y(t) will converge to zero in finite time t2. Based on the above discussion, once y(t) converges to zero in finite time, the subsystem (3) will be asymptotically stable about the origin x= 0 and z= 0.
Remark 3 In Ref. [39], the same control scheme for fractional-order economical system (2) is presented. However, when the states are driven to the designed sliding surface
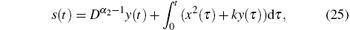
it satisfies s= 0 and ṡ = 0, i.e.,

Obviously, typical fractional-order stability theorem does not apply to nonlinear differential equation (26), and the given sliding surface (25) does not have a desired system dynamics. By comparison, in this paper, the proposed sliding surface (7) can satisfy the finite time stability of system state y(t), which can further obtain the asymptotical stability of system states x(t) and z(t). Therefore, the main results of this paper are more reasonable and rigorous than the existing results.[39]
Considering that system (4) is perturbed by parameter uncertainty and external disturbance, which comes from the introduction of the single controller u(t), the systems can be expressed as follows:
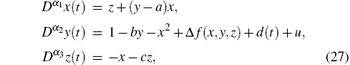
where Δ f(x, y, z) and d(t) are parameter uncertainty and external disturbance, respectively, which are assumed to be bounded as |Δ f(x, y, z)|< η 1 and |d(t)|< η 2 (η 1, η 2> 0). The following theorem will give sufficient conditions of finite time convergence to sliding surface s(t) for system (27) with parameter uncertainty and external disturbance.
Theorem 3 If system (27) is controlled with the following controller:

where k> 0, ξ > 0, and γ ∈ (0, 1) are constants, s(t) has the same form as (7), then the system state y(t) will converge to the sliding surface s(t)= 0 in finite time.
Proof Selecting a Lyapunov function in the form of V(t)= |s(t)| and the time derivative of V(t) is obtained as follows:
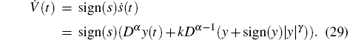
From Eqs. (27)– (29), we obtain
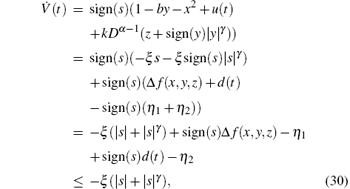
where the inequalities sign(s)Δ f(x, y, z)-η 1 ≤ |Δ f(x, y, z)|-η 1≤ 0 and sign(s)d(t)-η 2≤ |d(t)|-η 2≤ 0 are used. Obviously, the system state trajectories will converge to the sliding surface s(t)= 0 asymptotically. Similar to the proof of Theorem 1, we can also obtain the results that the sliding motion occurs in finite time. Referring to Eqs. (17)– (19), the reaching time t1 can be derived as

where t0 is the initial time. The detailed proof is similar to that of Theorem 1, which is omitted here. We complete the proof.
Once the states of system (27) reach the sliding surface (7), the desired convergence characteristic (state y(t) converges to zero in finite time) will be subsequently achieved, and then the asymptotical stability of states x(t) and z(t) can be obtained by the designed sliding surface (7).
In the simulation, two illustrative examples are given to verify and demonstrate the effectiveness of the proposed method, and the time-domain numerical algorithm based on predictor– corrector scheme[39] is used for simulations.
According to Ref. [39], the system is chaotic when α 1= α 2= α 3= 0.9 and (a, b, c)= (1, 0.1, 1). The chaotic trajectories of the fractional-order economical system without the controller u(t) are shown in Fig. 1. By Theorems 1 and 2, the time response of system (4) and the sliding surface are shown in Figs. 2 and 3, respectively. Throughout the simulation, the initial condition is taken as [1, 1, − 1]T, and the control parameters in Eqs. (7) and (21) are chosen as k= 0.1, γ = 0.95, and ξ = 0.5.
 | Fig. 1. The chaotic trajectories of the fractional-order economical system (2). |
Let the parameter uncertainty be Δ f(x, y, z)= 0.5sin(π x)cos(π y)sin(2π z) and the external disturbance be d(t)= 0.1cos(2t), where |Δ f(x, y, z)|≤ η 1= 0.5 and |d(t)|≤ η 2= 0.1. Based on Theorems 1 and 3, the time response of system (27) and the sliding surface are shown in Figs. 4 and 5, respectively. Throughout the simulation, the initial condition is taken as [1, 1, − 1]T, and the control parameters in Eqs. (7) and (28) are chosen as k= 0.1, γ = 0.95, and ξ = 0.5. Note that the introduction of parameter uncertainty and external disturbance may change the chaotic behavior of the original fractional-order chaotic economical system, and this change cannot affect the control performance. From the simulation results (see Fig. 4), the proposed controller (28) can still realize the robust control of the original fractional-order economical system.
 | Fig. 2. Time response of system (4). (a) x(t), (b) y(t), (c) z(t). |
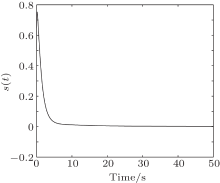 | Fig. 3. Time response of sliding mode surface (7). |
 | Fig. 4. Time response of system (27). (a) x(t), (b) y(t), (c) z(t). |
 | Fig. 5. Time response of sliding mode surface (7). |
In this paper, we present a modified sliding mode control method to stabilize typical fractional-order chaotic economical systems. By constructing an efficient sliding mode surface and control law, some effective and practical sufficient conditions are presented to guarantee the system dynamics with or without uncertainty and external disturbance can converge to the origin asymptotically. Finally, two numerical examples for nominal and uncertain fractional-order economical systems are given to demonstrate the effectiveness of the method.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|


