†Corresponding author. E-mail: cgshao@mail.hust.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2010CB832800), the National Natural Science Foundation of China (Grant Nos. 11175160 and 11275075), and the Natural Science Foundation of Key Projects of Hubei Province, China (Grant No. 2013CFA045).
The environmental noise can restrict the accuracy of period estimation since the torsion pendulum is sensitive to weak forces. Two typical models for the environmental noise are proposed to make an evaluation. Generally, the stationary environmental noise is modeled as a white noise, and contributes to the period uncertainty as a function of the initial amplitude, the quality factor, the variance of noise and the time length. As to a sudden sharp disturbance acting on the pendulum, a narrow impulse model is constructed. It results in a sharp jump in the phase difference, which can be excluded with the 3 σ criterion for a correction. An experimental data analysis for the measurement of the gravitational constant G with the time-of-swing method shows that the period uncertainty due to the environmental noise is about one and a half times the fundamental thermal noise limit. Though this result is dependent on the ambient environment, the analysis is instructive to improve the measurement accuracy of experiments.
The measurement of a torsion pendulum’ s period is of great importance for some gravitational experiments.[1] For example, the measurement of the Newtonian gravitational constant G with the time-of-swing method[2– 8] is based on measuring periods of the pendulum with two configurations of source masses, and the measurement accuracy of the period directly restricts the measurement accuracy of G.
As a highly sensitive device, the sensitivity and precision of the torsion pendulum are limited by noise of different origins, which can be generally divided into two categories. One is called the intrinsic noise, such as the thermal noise due to the internal losses in the suspension system, which sets the most fundamental limit to the period of the pendulum.[9– 14] The other is called the external noise, namely, the environmental noise, which is a general term for different noise sources including the seismic noise, the local gravitational disturbances, the local magnetic field, [15] the Earth’ s rotation[16] and other issues. In previous works, the thermal noise limit on the period of the pendulum has been presented in detail, being a function of the initial oscillation amplitude, the quality factor, the ambient temperature and the length of measurement time.[8, 12, 14] As to the environmental seismic noise, related papers have focused on the effect of the coupling of swing modes excited by it on the torsional mode. The frequencies of the coupled modes are somewhat different from the natural frequency of the torsion pendulum, and these modes can be successfully suppressed by the amplitude or frequency suppression method.[17– 19] In this condition, it is reasonable to think about the period uncertainty due to the resonance mode excited by the stochastic and stationary environmental noise, which has not been referred; except for it, the special condition when a sudden sharp shock occurs should be considered. When compared with the thermal noise limit, the quantitative analysis for the environmental noise’ s influence on the period is essential. In addition, how to suppress this influence still needs further research.
In this paper, two typical models are respectively proposed to make an evaluation of the influence of environmental noise on the torsion pendulum’ s period. There are many methods to extract the pendulum’ s period.[20– 25] The correlation method is used in our analysis since it is insensitive to drift, damping, as well as higher order harmonics. According to the data processing rules, [26] the data polluted by sudden sharp external disturbances should be excluded with the 3σ criterion, which states that for a normal distribution, nearly all values (99.7% ) lie within 3 standard derivations of the mean, and the data falling outside the range should be picked out and rejected. After the correction, the period uncertainty due to the stochastic and stationary environmental noise is calculated, which is a function of the initial amplitude, the quality factor, the variance of noise, and the time length. An experimental data analysis in measuring G with the time-of-swing method shows that the period uncertainty due to the environmental noise is about one and a half times of the thermal noise limit. Though this result is dependent on the experimental environment, the mathematical analysis is instructive for improvement of the measurement accuracy.
Subject to the velocity damping, the equation of motion for a free torsion pendulum is

where I is the moment of inertia, γ is the friction parameter, and K is the fiber torsion constant. The torsion constant is an intrinsic property of the torsion fiber, and its value changes with time due to the aging effect.[25, 26] In linear approximation, the torsion constant can be expressed as K0 (1 + α t), where K0 is the torsion constant at the initial time t = 0, and α represents the aging effect. Accordingly, a more realistic description of the motion of the torsion pendulum might be
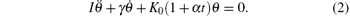
Noting the equivalence γ /(2I) = β and 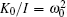
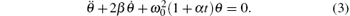
Setting α = 0, there comes the familiar differential equation 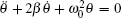
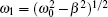
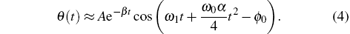
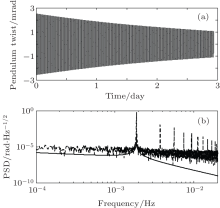 | Fig. 1. The rotational angle (a) and its power spectral density (b): the PSD of the thermal noise is plotted by the solid line, while that of the signal is plotted by the dash line. |
To extract the period of the pendulum with the correlation method, a standard function cos(ω rt) with ω r ≈ ω 1 is chosen as a reference signal to calculate the phase difference ϕ j (j= 0, 1, … , m– 1) with respect to θ (t) at the j-th period, where m is the number of periods. For each period, the phase difference ϕ j is determined by

where Tr = 2π /ω r is the reference period. By Substituting Eq. (4) into Eq. (5) and choosing the initial phase in | ϕ 0| ≪ 1, ϕ j is further calculated as
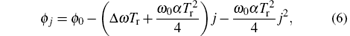
with Δ ω = ω 1 − ω r.
As the period changes with respect to time, the period at half the measuring time is determined as a rough estimation for the whole oscillations. To simplify the calculation, a shift of the range of j with − (m− 1)/2 is processed. Then a quadratic polynomial fitting of the phase difference ϕ j is performed to obtain the coefficients
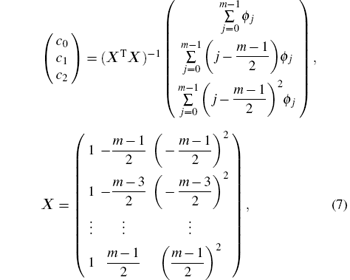
such that the center period is estimated to be

The torsion pendulum responses to environmental noise including seismic noise, local gravitational disturbances, the local magnetic field, the Earth’ s rotation, and other issues. Therefore, its period is somehow influenced by these disturbances. To make an evaluation, two typical models are proposed based on the character of noise in the following subsections.
Generally, environmental noise can be viewed as stochastic and stationary. In this case, it can be modeled by a random fluctuation torque τ e(t), which has a statistical property of the white noise. Namely, it has zero mean ⟨ τ e(t)⟩ = 0 and the autocorrelation function ⟨ τ e(t1)τ e(t2)⟩ = Dδ (t1 − t2). The equation of motion changes from Eq. (3) to

The solution is a linear combination of the corresponding homogeneous differential equation in the form of Eq. (3) and a particular solution due to the external torque. Accordingly, It has the form as

It is difficult to get an ideal analytic expression for the particular solution θ e(t). Considering that the noise is random and the aging effect is weak as mentioned above, the analysis could focus on the main part of the response to the noise. Then, a first-order approximation for the particular solution is obtained by ignoring the coefficient α

By calculation, ⟨ θ e(t)⟩ = 0, and the responses at different times are correlated
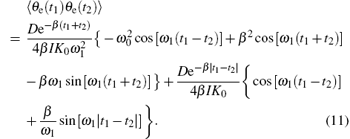
As the oscillations of the pendulum are disturbed by θ e(t), the phase difference calculated by the correlation method is then influenced by a random phase noise δ ϕ j, which is

and ϕ j can be further expressed as
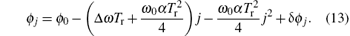
By substituting Eq. (10) into Eq. (12), and combining the result with Eq. (11), the autocorrelation function of δ ϕ j can be calculated. When taking an approximation ω r ≈ ω 1, the result is
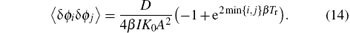
Consequently, when substituting Eq. (13) into Eq. (7), the coefficient c1 is biased by
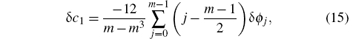
and the period is influenced by
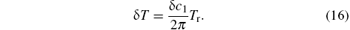
Finally, the uncertainty in period due to the stationary environmental noise is
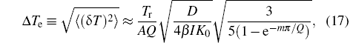
where Q is the quality factor determined by ω 0/2β .
Except for the stationary model, another model should be constructed for the special condition when a sudden sharp shock acts on the torsion pendulum, such as in high level seismic noise. This instant shock can be treated as a narrow impulse described by a δ (t) function, and the motion of the pendulum is

where ti is the time when the shock forces on the pendulum with magnitude σ e.
Before time ti, the oscillations of the pendulum are described by Eq. (4); after time ti, the initial conditions to solve the equation are changed. Therefore, the rotational angle of the pendulum during the whole measuring time is a piecewise function. With a hypothesis that the aging effect and the damping are weak when compared with the shock, the angle can be
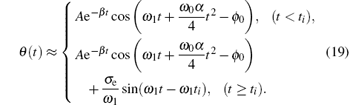
According to Eq. (5), the phase difference is also a piecewise function
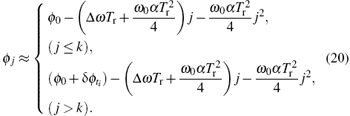
The relationship between time ti and k can be noted by ti = kTr + Δ ti, where k varies from 0 to m− 1, Δ ti varies from 0 to Tr, and both are independent from each other.
The discontinuity in phase difference, noted by δ ϕ ti, reflects the character of the external shock. Performing a quadratic polynomial fitting of the phase difference in Eq. (20), the linear coefficient c1 is then influenced by

and the period is biased in the same form of Eq. (16).
As mentioned in previous works, the thermal noise is a fundamental limit in the determination of the pendulum’ s period. The thermal fluctuation torque τ th(t) acting on the pendulum is also viewed as a white noise. According to the fluctuation dissipation theorem, [27] the expectation value and the autocorrelation function can be respectively
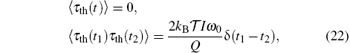
where kB is the Boltzmann constant and 𝓣 is the ambient temperature.
Comparing the property of the thermal noise with that of the stationary environmental noise, they are the same except that D is known as 2kB𝓣 Iω 0/Q for the thermal noise. Similarly, the thermal noise results in the period uncertainty:

When the rotational angle is recorded, the noise in the angular-deflection readout system is added in. It can be described by a white noise θ ro(t) with zero mean and the autocorrelation function
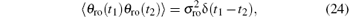
where 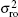
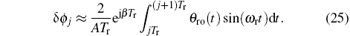
Consequently,
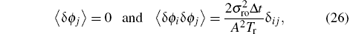
where Δ t is the sample interval.
Combining Eqs. (25) and (26) with Eq. (15), the uncertainty in period due to the readout noise is

The relationship between the variance and the power spectral density of the readout noise is σ ro = θ ro(ω )Δ t− 1/2. Combining it with Eq. (27) yields an equivalent expression as
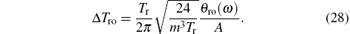
In the experiment of measuring G with the time-of-swing method, [26] all the data are taken at a regular interval of Δ t = 0.5 s. One typical angle-time data set of the pendulum in about three days and its power spectral density (PSD) are shown in Fig. 1. The initial amplitude of the rotational angle of the pendulum is about 2.5 mrad. The period is about 532.5 s, with the total period number m ∼ 500.
In this system, the moment of inertia of the pendulum I is about 4.5 × 10− 5 kg· m2, and the pendulum is suspended in a high vacuum with Q of ∼ 1700. The ambient temperature is 𝓣 ∼ 300 K. According to Eq. (23), Δ Tth due to the thermal noise is about 0.10 ms. From the PSD, θ ro (ω ) for the readout noise is measured about 10− 5 rad· Hz− 1/2, so Δ Tro due to the readout noise in Eq. (28) is 0.006 ms, which is one order less than the thermal noise limit.
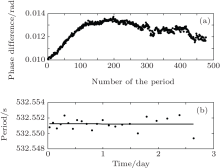
To determine the pendulum’ s period with the standard procedure, the phase difference is shown in the upper part of Fig. 2. By performing a quadratic polynomial fitting to it, the period is determined as in Eq. (8). In order to know the tendency of the period, the phase difference is divided into small parts. In each part, a linear fitting is performed to get the period at the midpoint of the corresponding data segment. The time-period sequence is illustrated by dots in the lower part of Fig. 2. A linear fitting of these obtained periods is represented by the solid line with the slope − 0.02 ms/day, showing that the period decreases with time as a result of the aging effect. The vibration is due to different noise sources, and the statistical uncertainty in the period is evaluated as Δ Tmeas = 0.18 ms, about two times of the thermal noise limit.
Attributed to a variety of noise sources, the statistical uncertainty can be seen as a combined uncertainty, which is equal to the positive square root of the combined variance obtained from all variance and covariance components. As the statistical noise mainly consists of the thermal noise, the readout noise and the environmental noise, a rough estimate of the uncertainty due to the environmental noise can be Δ Te = 0.15 ms, which is larger than the thermal noise limit. Combining this value with Eq. (17), the variance of the stationary external noise can be evaluated.
The variation of the phase difference shown in Fig. 2 reflects the influence of the noise. Usually, before a quadratic polynomial fitting to the phase difference is taken, an examination on ϕ j is performed to see if there is a gross error in the data, just by using the 3σ criterion in the sequence Δ ϕ j = ϕ j − ϕ j− 1. Further, the polluted phase is excluded as a correction; or else, the period should be badly influenced.
As an example, in Fig. 3, there is a sharp jump in the phase difference. This data may be seriously polluted by the external disturbances, such as a sudden disturbance from the seismic noise. To make an evaluation, the narrow impulse model in section 3.2 is used. The data is cutoff at the 337th point, with a jump from − 0.0113 rad to − 0.0097 rad. Thus, the parameters in Eq. (21) are k = 337, m = 480 and δ ϕ ti = 1.6 mrad. Accordingly, the bias on the period is Δ Te = 0.36 ms, which is considerable.
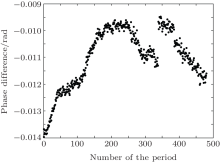 | Fig. 3. The phase difference calculated by the correlation method for one data set. It is cutoff at the 337th period in the total 480 periods. |
In conclusion, if there is a sudden disturbance from the environmental noise, the influence can be detected and corrected, so the analysis of period uncertainty due to environmental noise comes back to the stationary noise model. In the experiment of measuring G with the time-of-swing method, the uncertainty in the period due to the environmental noise contributes to the uncertainty in G with
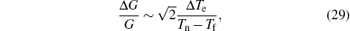
where Tn and Tf represent the periods of the pendulum at the near and the far configurations respectively, and Tn − Tf ≈ 3.2 s. Taking the value Δ Te = 0.15 ms, the uncertainty in G is about 66 ppm, if only one data set is used. When the measurements from the near to far positions are repeated N times, the uncertainty in G decreases to 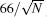
Except for the thermal noise in the torsion pendulum and the noise in the angular-deflection readout system, the environmental noise can restrict the accuracy of period estimation, which is important for some gravitational experiments. Two typical models are proposed to make an evaluation of its influence. The seriously polluted data due to a sudden sharp disturbance from the environmental noise can be excluded with the 3σ criterion for a correction. Mostly, the stochastic and stationary environmental noise generates an external torque similar to the thermal noise, and contributes to the uncertainty in the period as a function of the initial amplitude, the quality factor, the variance of noise, and the length of measuring time.
Experimental data analysis for the measurement of G with the time-of-swing method shows that the uncertainty in the period due to the environmental noise is larger than that due to the thermal noise, which sets the most fundamental limit to experiments. Though this result is related to the ambient environment, the analysis is instructive to improve the measurement accuracy, and different measures can be taken. For example, an enhanced isolation from the ground vibration due to the seismic noise is necessary. In addition, choosing a larger amplitude for the oscillations will lead to a smaller uncertainty, with the nonlinear effect[28] considered.
The authors would like to thank the Center for Gravitational Experiments of HUST for providing the experimental data.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|