†Corresponding author. E-mail: wangrui@zjou.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11304281) and the Natural Science Foundation of Zhejiang Province, China (Grant No. LY13D060002).
We investigate the topological phase marked by the Thouless–Kohmoto–Nightingale–Nijs (TKNN) number and the phase transitions driven by the next nearest neighbor (NNN) hopping in noncentrosymmetric cold Fermi gases, both spin-singlet pairing and spin-triplet pairing are considered. There exists a critical
Topological phases and topological phase transitions are two of the most active research areas in physics.[1– 5] These topological states, which have a full gap in the bulk and topologically protected gapless states on the boundary, [6– 9] are usually characterized by some global topological quantum numbers, such as the Thouless– Kohmoto– Nightingale– Nijs (TKNN) number.[10] The topological order supports the existence of chiral Majorana edge modes, and the vortices with Majorana fermion modes are neither fermions nor bosons but non-Abelian anyons, which obey the non-Abelian statistics.[11– 13] Majorana fermion could be exploited as a decoherence qubit and has attracted much attention for its remarkable application in fault-tolerant topological quantum computation.[14– 16] Sato et al. have pointed out that an s-wave superconductor with Rashba spin– orbit coupling (SOC) could have a non-Abelian topological phase, [11] where a large Zeeman magnetic field is essentially needed. It was also reported that a spin-triplet superconductor with broken time-reversal symmetry possesses a zero-energy Majorana mode, and hence can realize a non-Abelian topological phase in the presence of Rashba SOC.[17, 18]
Two-dimensional (2D) ultra-cold Fermi gases can be utilized to simulate many other systems due to their controllability and operability.[19– 24] Recently, the experimental realization of SOC in ultra-cold atoms was reported.[25– 29] This opens a completely new avenue for exploring many-body physics in the presence of SOC. The simplest way to realize the SOC in ultra-cold Fermi gases is based on the p-wave superfluid of degenerate Fermi gases by means of the p-wave Feshbach resonance.[22] This method is a direct way to realize the simulation, but the very short lifetimes of the p-wave pairs and molecules are a top challenge. Zhang et al. suggested that an artificially generated SOC could create an effective px + ipy topological superfluid from an s-wave interaction.[25, 30, 31]
In most realized square optical lattices, the next nearest neighbor (NNN) hopping (along the diagonal) t′ is much smaller than the nearest neighbor (NN) hopping t and it is instructive to set t′ = 0. Recently, several experimental and theoretical explorations showed that by shaking the optical lattice, the ratio t′ /t can be varied in a very large range. It was reported that a periodic shaking with amplitude V0 and frequency ω can lead to a renormalization of the NN hopping, which becomes multiplied by a Bessel function, teff = tJ0(V0/ħ ω ). On the other hand, the NNN hopping can also be renormalized by a Bessel function with a different argument. These would lead to a full range of possible values for the ratio 
The organization of this paper is as follows. In Section 2, we give our model and the condition of gap closing. Then the topological phase marked by the TKNN number ITKNN and the quantum phase transitions driven by the NNN hopping are discussed in detail. In Section 3, we investigate the properties of the energy spectrum with edge states to prove the bulk– boundary correspondence and the Majorana zero modes. The final section is a summary.
The cold Fermi gases with Rashba SOC on an isotropic 2D square optical lattice can be realized by adjusting the intensities of the lasers.[25, 26] Both spin-singlet component Δ s and spin-triplet component Δ p are considered for the parity mixing of Cooper pairs in our model. With the NNN hopping, the Hamiltonian in real space can written as[17]

Here the first term is the NN hopping with 
To explore the gapless condition, we will work in the momentum space. After the Fourier transformation and by choosing the Nambu spinor basis 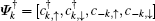
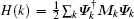
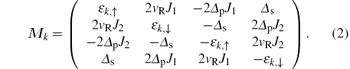
Here J1 = sinky + i sinkx, J2 = sinky – i sinkx, and ε k, ↑ and ε k, ↓ stand for the kinetic energy
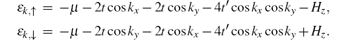
Diagonalizing matrix Mk and defining δ ε k = ε k, ↑ – ε k, ↓ , we can obtain the band structure
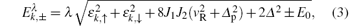
where λ = ± 1 correspond to the electrons (conduction band) and holes (valence band), and
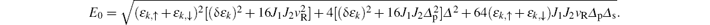
The gap of the system closes only when 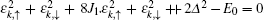
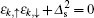

In the above conditions, Hz > Δ s is required. When one of these conditions is satisfied, the energy gap closes. It is noticed that all the conditions do not depend on the Rashba SOC and the spin-triplet pairing. Since the gap closing only happens at k = (0, 0), (0, π ), (π , 0), (π , π ) where both Rashba SOC vR(sinky ± i sinkx) and the spin-triplet pairing Δ p(sinky ± i sinkx) are zero. The spin-triplet pairing could bring an obvious effect on the edge states, which we will discuss later.
For our 2D time-reversal-symmetry-broken system, TKNN number ITKNN is an important topological number, which plays a central role in topological nature.[10] To obtain the TKNN number, we shall begin with the Schrö dinger equation

where | ϕ n(k)⟩ is the normalized wave function of the n-th band. In terms of the gauge field
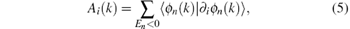
the Berry connection can be written as F12(k) = ε ij∂ iAj(k) = ∂ xAy(k) – ∂ yAx(k). Then, we have
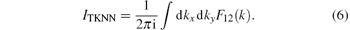
Here, the derivative ∂ i stands for ∂ /∂ ki with i = x, y and the integral is around the first Brillouin zone. It is noticed that the sum in Eq. (5) is restricted to the occupied bands.
Generally, a nonzero TKNN number allows both non-Abelian topological order which is characterized by the non-Abelian statistics and Abelian topological order without non-Abelian statistics. If the TKNN number is odd, the system is in a non-Abelian topological phase and there exists an odd number of Majorana zero modes in a vortex, which implies that the vortex is a non-Abelain anyon.[11, 12] If the TKNN number is even, the system is in an Abelian topological phase and there is no non-Abelain anyon. If the TKNN number is zero, the system will be in a topological trivial phase.
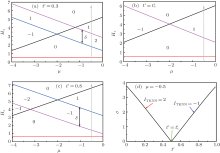
Figure 1 shows the topological phase diagram, where the number in each region is the TKNN number, and the unit of energy is set as t. The red horizontal line in each panel labels Δ s, and the magnetic field must be larger than Δ s. The parameters used here are Δ s = 0.6, Δ p = 0.8, and vR = 0.5. Figure 1(a), which is for the case of t′ = 0.3, shows there are four regions that are topologically distinct. The gap between two boundaries can defined as the height of the topological phase, which is shown in Figs. 1(a) and 1(c), where δ = Δ Hz = | Hz2 – Hz3| , and Hz2 and Hz3 are calculated from the second and the third equations in Eq. (4). For a given μ , δ will be adjusted only by t′ , and there exists a critical 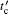

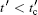
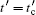

The system is periodic at the y direction and has two open boundaries at ix = 0 and ix = 100. By numerically diagonalizing Hamiltonian (1) in real space, the excitation spectrum E as a function of ky can be obtained.
Figure 2 shows the energy spectrum with edge states of 2D cold Fermi gases, both spin-singlet pairing and spin-triplet pairing are considered. Generally, a topologically nontrivial bulk guarantees the existence of topologically stable gapless edge states on the boundaries. For the 2D cold Fermi gases with a magnetic field breaking the time-reversal symmetry while having the particle– hole symmetry, the gapless edge states are chiral Majorana fermion modes. The parameters used here are Δ s = 0.6, Δ p = 0.8, and vR = 0.5. In Fig. 1(a), we show that as the magnetic field increases, the system will go through four quantum phases sequentially (see the gray line, where μ = − 0.5). Their spectra are correspondingly shown in Figs. 2(a)– 2(d). When t′ = 0.8, the phase in Fig. 2(b) changes to that in Fig. 2(e), corresponding to the phase transition in Fig. 1(d). Figure 2(f) is for the case of t′ = 0.3, μ = − 3, and Hz = 3 with the TKNN number ITKNN = − 1.
It is noteworthy that although figures 2(c), 2(e), and 2(f) are all for the non-Abelian topological phase with an odd TKNN number, the numbers of Majorana zero modes in the figures are quite different. There is only one Majorana zero mode in Figs. 2(c) and 2(f), while there are three Majorana zero modes in Fig. 2(e). Normally, a zero TKNN number corresponds to a topological trivial phase, which indicates that there exists no gapless state, such as the case in Fig. 2(d). However, there are two gapless states in Fig. 2(a). This is a bit surprising because the magnetic field breaks the time-reversal symmetry and the TKNN number is still zero in this region. This is not the first time a gapless state has been found in a region marked by ITKNN = 0, similar results can be found in Ref. [12]. In Fig. 2(b), when the TKNN number is even, there are an even number of gapless states in the spectrum and the system is in an Abelian phase.
In Eq. (4), we show that the spin-triplet pairing Δ p does not contribute to the gap closing and the phase diagram. Under the condition of t′ = 0.3, the phase diagram for Δ p = 0 is the same as that shown in Fig. 1(a), where we have set Δ p = 0.8. In Fig. 3, we illustrate the energy spectrum with edge states of the 2D Fermi gases with pure spin-singlet pairing. The parameters used here are Δ s = 0.6, Δ p = 0, and vR = 0.5. For comparison with Figs. 2(a)– 2(d), four spectra under the condition of μ = − 0.5 are given correspondingly in Figs. 3(a)– 3(d). There is an obvious difference between Figs. 3(a) and 2(a), both are all for the trivial quantum phase marked by ITKNN = 0, but there are no gapless states when the spin-triplet pairing is absent in Fig. 3(a). The spin-triplet pairing does not contribute to the gapless condition, but it can induce gapless states in a topological trivial system.
When the TKNN number is odd (even), an odd (even) number of Majorana zero modes always exists in the spectrum. When the TKNN number is zero, Majorana zero modes do (not) exist when both spin-singlet and spin-triplet pairings are considered (when only the spin-singlet pairing is considered) in the presence of both Rashba SOC and a magnetic field. When we focus on the non-Abelian topological phase and the non-Abelian anyon, the index (− 1)ITKNN is of particular interest, since it gives a hallmark of the non-Abelian topological phase, i.e., when (− 1)ITKNN = − 1, it indicates that the phase is a non-Abelian topological one and there is an odd number of Majorana zero modes in a vortex, which implies that the vortex is a non-Abelian anyon.
For the spin-singlet pairing and spin-triplet pairing cold Fermi gases on an isotropic 2D square optical lattice, considering both the NNN hopping and the Rashba SOC, we investigate the gapless condition and the phase diagram in detail. By using TKNN number ITKNN as an index of the quantum phase, we study the topological nature and the quantum phase transitions controlled by the NNN hopping in this 2D cold Fermi gas. There exists a critical 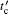
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|