†Corresponding author. E-mail: baqi2002@163.com
*Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LQ13A010014), the National Natural Science Foundation of China (Grant Nos. 11326164, 11401528, and 11275072), and the Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20120076110024).
In this paper, nonlocal symmetries defined by bilinear Bäcklund transformation for bilinear potential KdV (pKdV) equation are obtained. By introducing an auxiliary variable which just satisfies the Schwartzian form of KdV (SKdV) equation, the nonlocal symmetry is localized and the Levi transformation is presented. Besides, based on three different types of nonlocal symmetries for potential KdV equation, three sets of negative pKdV hierarchies along with their bilinear forms are constructed. An impressive result is that the coefficients of the third type of (bilinear) negative pKdV hierarchy ( N > 0) are variable, which are obtained via introducing an arbitrary parameter by considering the translation invariance of the pKdV equation.
Lie group theory[1, 2] is one of the most effective methods for seeking exact and analytic solutions of nonlinear partial differential equations (PDEs). Starting from Lie point symmetries, one can compute corresponding finite transformations and similar reductions to obtain explicit solutions directly. With the development of integrable systems and soliton theory, a variety of nonlocal symmetries have been intensely investigated in the literature. For example, a type of nonlocal symmetries which are related to Lax pair of integrable equations, that is so-called eigenfunction symmetries, [3– 8] have played an important role in the topics of symmetry constraints, soliton equations with sources, positive and negative hierarchies, etc.
However, one usually cannot apply nonlocal symmetries directly to get explicit solutions via the classical Lie group method. One feasible way is to localize nonlocal symmetries by introducing another auxiliary variables into an extended system. In fact, this generalization of the concept of nonlocal symmetries by including pseudo-potentials was devised by Edelen, [9] Krasil’ shchik and Vinogradov[10, 11] in the 1980s by using their theory of coverings of differential equations. Galas[12] rederived one-soliton solutions for the KdV equation, Dym equation and AKNS system equations based on nonlocal symmetries of this sort. As an application of nonlocal symmetries for the bilinear KP equation and bilinear BKP equation, Hu et al.[13] derived two types of bilinear negative KP and bilinear negative BKP hierarchies, respectively. Recently the nonlocal symmetries are receiving great interest and much progress has been made on this topic. In our early two papers, [14, 15] a class of nonlocal symmetries of the (potential) KdV equation in elegant and compact form are derived from Bä cklund transformation and Darboux transformation. Then we use these nonlocal symmetries to get abundant explicit solutions, especially the new interaction excitations between solitary waves and cnoidal waves, and to construct some integral models both in finite and infinite dimensions. One can also obtain the binary Darboux transformation starting from the nonlocal symmetries, by solving an initial value problem via introducing a suitable prolonged system.[16] In latter studies, based on this nonlocal symmetries approach, kinds of novel exact interaction solutions among solitons and other complicated waves have also been found for mKdV equation, [17] AKNS system, [18] KP equation, [19] the Hirota– Satsuma coupled Korteweg-de Vries system, [20] the (2+ 1) dimensional modified generalized long dispersive wave equation[21] and the nonlinear Schrö dinger (NLS) equation.[22] In Ref. [23], Bluman and Yang introduced a new and complementary method for constructing nonlocally related PDE systems, which was on the basis of each point symmetry.
In this paper, our aim is to investigate nonlocal symmetries defined by bilinear Bä cklund transformation and their corresponding applications for bilinear potential KdV (pKdV) equation. In Section 2, the nonlocal symmetry is localized and the corresponding prolonged system for bilinear KdV equation is found. An impressive observation is that the process of localization also leads to the Schwartzian form of KdV equation, where the Schwartzian variable is realized by two solutions of the bilinear pKdV equation. Then via Lie’ s first theorem, the Levi transformation (the second Bä cklund transformation) is presented to give transformed solutions from trivial ones. In Section 3, combining different types of nonlocal symmetries with the bilinear Bä cklund transformation of pKdV equation, three sets of negative pKdV hierarchies along with their bilinear forms are constructed. Section 4 is a short summary and discussion.
It is known that for KdV equation

we have the potential KdV equation given by
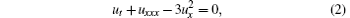
with ω = ux.
Furthermore, for Eq. (2), there is the following Bä cklund transformation:[25]
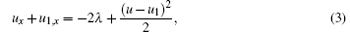
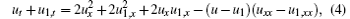
with λ being an arbitrary parameter. The compatible condition u1, xt = u1, tx of Eqs. (3) and (4) is just pKdV equation (2). Under the transformations u = − 2 (ln f)x and u1 = − 2 (ln g)x, the pKdV equation and its Bä cklund transformation can be expressed as bilinear forms, saying

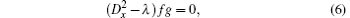
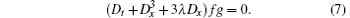
The well-known Hirota’ s bilinear operator 

In our early paper, [14] we obtained a nonlocal symmetry of u for pKdV equation given by
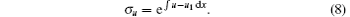
Here, the nonlocal symmetry of f for bilinear KdV equation can be derived from Eq. (8), i.e.,
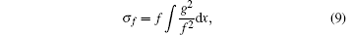
where f and g satisfy bilinear Bä cklund transformation (6) and (7).
Clearly, the symmetry equation (9) for f is nonlocal. To localize Eq. (9), we introduce g1 ≡ g1(x, t) by
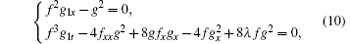
which leads nonlocal symmetry equation (9) to
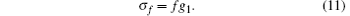
Then, by solving symmetry equations (6), (7), and (10) given by
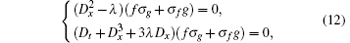
and
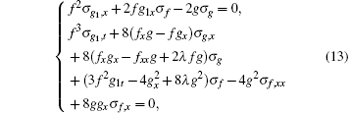
we obtain the corresponding symmetries σ g and σ g1 of g and g1 respectively, saying
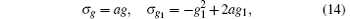
with a being an arbitrary constant.
From Eqs. (11) and (14), one can see that the prolongation of nonlocal symmetry equation (9) is closed after covering three dependent variables f, g, and g1. Hence, the final prolonged system containing Eqs. (5), (6), (7), and (10) is found, which has the following Lie point symmetry

Due to Eq. (15) and Lie’ s first theorem, solving the following initial value problem:
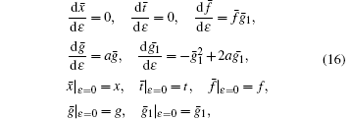
yields the finite symmetry transformations
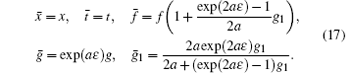
Remark 1 The bilinear Bä cklund transformation (6) and (7) in itself suggests a finite transformation from a solution f to another one g while the obtained finite transformation (17) arrives at a third solution f̄ . Actually, the transformation (17) is just the so-called Levi transformation or the second type of Bä cklund transformation.[24] This result shows the fact that two kinds of Bä cklund transformation possess the same infinitesimal form (9).
Remark 2 The form of σ g1 in Eq. (14) embodies the Mö bious (conformal) invariance property
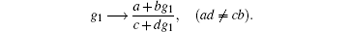
Actually, one can check that the introduced invariant g1 is nothing but just satisfy the Schwartzian form of KdV equation (SKdV equation)
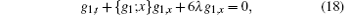
where {g1; x} = (g1, xxx/g1, x) – 3(g1, xx/g1, x)2/2 is the Schwartzian derivative. Here, the Schwartzian variable g1 shown in Eq. (10) is determined by the solutions {f, g} of the biliear Bä cklund transformation.
Now by force of the finite symmetry transformation equation (17), one can get new solutions from any initial solutions. For example, we take the trivial solution f = f0. From Eqs. (6), (7), and (10) with 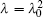
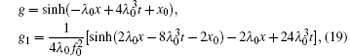
where λ 0, x0, and f0 are three constants. Substituting Eq. (19) into Eq. (17) leads to the transformed solution of Eq. (5)
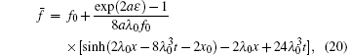
then to the solution of KdV equation (1), saying
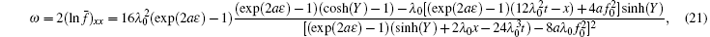
with 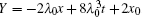
Next, according to the classical Lie group method, the complete Lie point symmetries of the whole system (5)– (7), and (10) can be obtained. Then, abundant group invariant solutions related to the nonlocal symmetry of the KdV equation, which are expressed in terms of rational function, Bessel functions, period functions and their combinations, can be obtained by following the same procedure in Refs. [14] and [15]. What is different from four variables in the prolonged system of Refs. [14] and [15] is here three dependent variables are enough to ensure the localization of the nonlocal symmetry.
The existence of infinitely many symmetries leads to the existence of integrable hierarchies and with the help of infinitely many nonlocal symmetries, one can extend the original system to its negative hierarchies.[13, 26] In the following, starting from the nonlocal symmetry (8) related to Bä cklund transformation of Eq. (2), three sets of negative pKdV hierarchies are constructed and their corresponding bilinear forms are also presented.
Based on the nonlocal symmetry (8), a set of negative pKdV hierarchy is obtained, reading
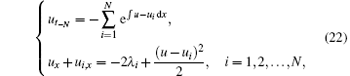
where λ i is an arbitrary constant. In particular, when N = 1, one has the first equation of negative pKdV hierarchy, namely

Here, we have instead t− 1 with t for simplicity. It is well known that the first negative flow in the KdV hierarchy is linked to Camassa– Holm equation via a hodograph transformation[27] or can be reduced to sinh-Gordon/sine-Gordon/Liouville equations.[28] Here, we can transform Eq. (23) into sine-Gordon and Liouville equations. In fact, by setting β ≡ β (x, t) = − ut, we can rewrite Eq. (18) in the form
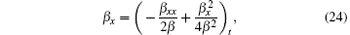
which can be integrated once with respect to x to give
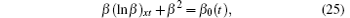
where β 0(t) is an arbitrary function of t.
Then, for non-zero β 0(t), one can rescale β to 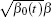
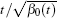
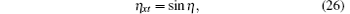
while for β 0(t) = 0, by setting β = − expη , equation (25) becomes the Liouville equation
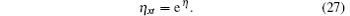
Furthermore, by virtue of the dependent variable transformation
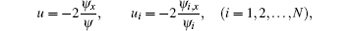
the negative pKdV hierarchy (22) is directly transformed into bilinear form

For the nonlocal symmetry (8) being dependent with arbitrary parameter λ , we may derive a type of negative pKdV hierarchy by expanding the dependent variable in power series of λ . In this case, we have
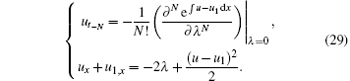
Under transformations u = − 2ψ x/ψ and u1 = − 2ψ 1x/ψ 1, the negative pKdV hierarchy (29) becomes
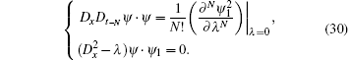
Let ψ 1 = ψ 1(λ ) has a formal series form
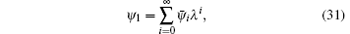
where 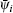
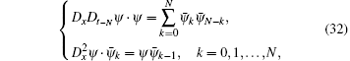
with 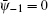
The negative KdV hierarchy in bilinear form (32) is just the special situation of the bilinear negative KP hierarchy for y = 0 in Ref. [13].
By considering the translation invariance of pKdV equation (2) under the transformation u → u+ c, another parameter μ can be introduced in the Bä cklund transformation (3) and (4) with u1 → u1 + μ , saying
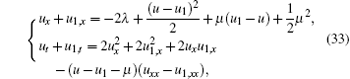
and the corresponding symmetry of u becomes σ ′ = e∫ u– u1– μ dx. In this case, we make λ = 0 and construct another negative pKdV hierarchy with the help of parameter μ . A novel set of negative pKdV hierarchy may be written down as follows:

Due to the same transformation u = − 2ψ x/ψ and u1 = − 2ψ 1, x/ψ 1, we have
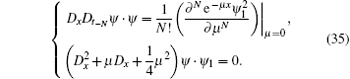
Let ψ 1 = ψ 1(μ ) has a formal series form
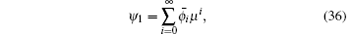
where 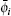
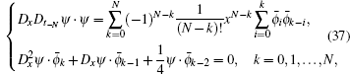
with 
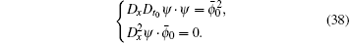
When N = 1, we have

When N = 2, we obtain
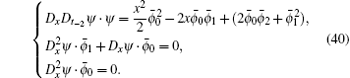
Remark 3 One can see that the coefficients of the third negative pKdV hierarchy (37) (N ≥ 1) are variable, which are exactly different from the other two cases.
In this paper, the nonlocal symmetry depending on bilinear Bä cklund transformation for bilinear pKdV equation is localized by covering three dependent variables, which differs from that in Ref. [14]. Via Lie’ s first theorem, we obtain a Levi transformation which possesses the same infinitesimal form (9) with the original bilinear Bä cklund transformation. Furthermore, on the basis of the nonlocal symmetry (8) of pKdV equation, three different types of nonlocal symmetries are built and then applied to construct three sets of negative pKdV hierarchies. In the third case, by considering translation invariance of the pKdV equation, another arbitrary parameter is introduced to get new nonlocal symmetries, which are then expanded in power series to derive negative hierarchy. It is remarked that the third type of (bilinear) pKdV negative hierarchy with variable coefficients is fresh and worthy of our further investigation. To search for nonlocal symmetries of integrable systems and then to apply them to obtain new results are both of considerable interest. We know that it is convenient to construct N-soltions from the bilinear forms of integrable eqautions. Combining bilinear equations or their bilinear Bä cklund transformation with nonlocal symmetries may provide a direct way for seeking exact interaction solutions among solitons and other background waves, the rogue waves solutions, the new integrable models in bilinear forms, the nonlocal or local conservation laws, etc. We believe that this approach would also play an important role in supersymmetry systems and discrete equations.
The authors thank Prof. Lou S Y for his helpful discussion.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|


