Corresponding author. E-mail: zhouzhehai@bistu.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 61108047 and 61475021), the Program for New Century Excellent Talents in University, China (Grant No. NCET-13-0667), and the Beijing Top Young Talents Support Program, China (Grant No. CIT&TCD201404113).
Multiple optical trapping with high-order axially symmetric polarized beams (ASPBs) is studied theoretically, and a scheme based on far-field optical trapping with ASPBs is first proposed. The focused fields and the corresponding gradient forces on Rayleigh dielectric particles are calculated for the scheme. The calculated results indicate that multiple ultra-small focused spots can be achieved, and multiple nanometer-sized particles with refractive index higher than the ambient can be trapped simultaneously near these focused spots, which are expected to enhance the capabilities of traditional optical trapping systems and provide a solution for massive multiple optical trapping of nanometer-sized particles.
In the past several years, particle manipulations have attracted much attention because of their wide applications in physics, chemistry, and biology.[1– 3] Especially, optical trapping by using cylindrical vector beams (CVBs) is demonstrated theoretically and experimentally for their better performances than those of traditional optical trapping with scalar beams. Zhan[4, 5] first theoretically studied the optical trapping of dielectric and metallic particles by using the radially polarized beams. Some theoretical and experimental results of optical trapping by using the CVBs were subsequently reported.[6– 12] In addition, some special trapping schemes have also been proposed by manipulating the polarization and phase distributions of incident CVBs in order to enhance the trapping performances, such as generation of optical chain[13] or optical cage, [14] or by using double-ring radially polarized beams[15] and higher-order radially polarized beams.[16] However, all these single-beam optical tweezers are almost used for individual particle trapping. Also, the very limited field-of-view of high numerical aperture objective lenses commonly employed for optical trapping restricts the number and the size of particles that can be trapped simultaneously. So, multiple optical trapping by using vector beams is expected to simultaneously trap multiple particles.
Meanwhile, some novel vector beams have been studied, which is expected to lead to some new effects and phenomena that can further expand the functionalities and enhance the capabilities of optical systems. One particular example is axially symmetric polarized beam (ASPB), a kind of space-variant linearly polarized beam with axial symmetry, and the symmetry axis is the propagation axis of the light beam.[17] Cylindrical vector beams (CVBs) are well known as ASPBs, which have been greatly studied and applied in many optical systems. To date, many methods have been reported to generate ASPBs, for example, using space-variant subwavelength metallic and dielectric gratings, [18, 19] liquid-crystal polarization converters, [17] and spatial light modulators (SLMs).[20] Meanwhile, the tightly focusing properties of such beams have also been studied theoretically, [21– 23] and the focused fields for high-order ASPBs (P > 1) present multi-focal-spot patterns, which are predicted to be useful for multiple optical trapping. However, to the best of our knowledge, detailed theoretical and experimental studies on multiple optical trapping by using the high-order ASPBs have not been presented to date.
In the paper, we numerically study multiple optical trapping by using high-order ASPBs. A scheme of far-field optical trapping is presented, and numerical simulation results in the Rayleigh regime of the trapping scheme are demonstrated. Unlike near-field optical trapping, far-field optical trapping is based on the far-field diffraction of beams, generally by using a tightly focused laser beam to trap and manipulate particles near the focused spots.[24] Compared with the reported schemes using CVBs, the scheme using high-order ASPBs can trap multiple nanometer-sized particles, for their focusing properties of multiple ultra-small focused spots, and the number and size of trapped particles can be manipulated by flexibly modifying the polarization order of the incident beam and numerical aperture of the lens, which provides a solution for the massively multiple trapping of nanometer-sized particles.
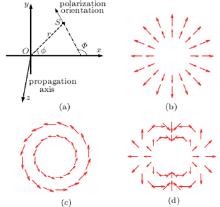
ASPBs have vector-vortex polarization profiles, and the beam propagation axis is its symmetric axis. As shown in Fig. 1(a), for ASPBs, the state of polarization (SoP) at any position (except the optical axis) on the beam cross section is linearly polarized, and the polarization orientation angle Φ (r, ϕ ) of the electric field depends only on the azimuthal angle as Φ (r, ϕ ) = P× ϕ + ϕ 0, where P is the polarization order number, ϕ is the azimuthal angle of the cylindrical coordinate system, and ϕ 0 is the initial polarization orientation for ϕ = 0. The phase distribution is uniform in the beam cross section (except the optical axis). Because the intensity at the optical axis is zero, the phase and polarization are uncertain. Figures 1(b) and 1(c) show the polarization distributions of radially polarized beams (P = 1, ϕ 0 = 0) and azimuthally polarized beams (P = 1, ϕ 0 = π /2) respectively, and figure 1(d) shows those of a kind of high order ASPB (P = 3, ϕ 0 = 0). The vector amplitude of the electric field can be expressed as
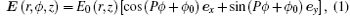
where r and ϕ are the cylindrical coordinates, E0 is the module of the vector amplitude, P is the polarization order, ϕ 0 is the initial azimuthal angle for ϕ = 0, and ex and ey are the unit vectors in the x axis and y axis.
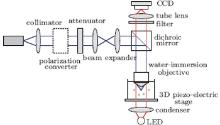
A far-field optical trapping scheme with high-order ASPBs is proposed as shown in Fig. 2. A Gaussian beam is emitted from a laser, and then collimated by a collimator. Then the collimated beam is incident onto a polarization converter, such as a subwavelength grating or a liquid-crystal polarization converter as mentioned above, [14– 17] using the polarization converter the high-order ASPBs can be generated. Then the generated beam is coupled into a water-immersion objective through a dichroic mirror. Micro-particles suspend in water. In addition, a narrow bandwidth LED source is used to image the trapped particles onto a CCD camera, and a short-pass filter is placed before the tube lens to block the trapping beam but the illumination beam can pass through the filter.
According to Richards & Wolf’ s vector diffraction theory, [25] the focused field of high-order ASPBs near focus in a cylindrical coordinate system can be expressed as
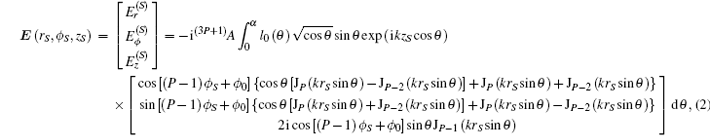
where S(rS, ϕ S, zS) is an observation point near focus; 

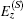
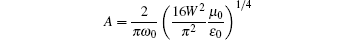
is a constant related to the amplitude and power of the incident beam, with W being the optical power of the incident beam, ω 0 the beam waist of the Gauss beam, μ 0 the magnetic permeability in a vacuum, and ε 0 the vacuum permittivity; k is the wavelength number; θ denotes the focusing angle (the angle between the optical axis and the propagation vector), so the relationship between the maximum of θ and numerical aperture (NA) of the objective lens is given by α = sin− 1(NA/n), with n being the refractive index of the surrounding medium; l0(θ ) is the pupil apodization function which represents the relative amplitude and phase of the incident beam.
In the simulations,
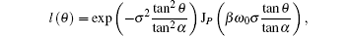
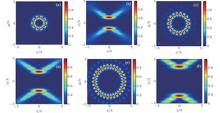
where σ is the pupil filling factor, the ratio of the pupil radius to the beam waist, which affects the focused field intensity distribution; [22]β is the modulation factor of the beam waist; P is the polarization order of the incident ASPB; σ = 1.0; ω 0 = 5 mm; β = 1 mm− 1. Figure 3 shows the focused field intensity distributions at focus [(a), (c), (e)] and through focus [(b), (d), (f)] for three kinds of high-order ASPBs withP = 6, 10, and 16, respectively. It is seen from the simulation results that multiple focused spots are formed and the number of spots is related to the polarization order P as 2× (P− 1), which indicates we can flexibly change the number of focused spots by modifying the polarization order of the incident ASPB. The focused spots are not spherically symmetric, but ellipsoid-shaped. The full width at half maximum (FWHM) values of spots in the radial direction are 0.62λ , 0.68λ , and 0.84λ , and in the azimuthal direction they are 0.42λ , 0.38λ , and 0.34λ for three kinds of ASPBs with P = 6, 10, and 16 respectively. The sizes of focused spots in the radial direction increase with the polarization order, but the sizes of focused spots in the azimuthal direction decrease with the increase of polarization order. The focusing properties of multiple ultra-small focal-spots are preferred to trap multiple nanometer-sized particles simultaneously.
For the results shown above, it is safe to say that the multiple focal-spot pattern originates from the spatial interference of the incident beam, which is naturally influenced by the polarization state of the incident beam.
As is well known, tightly focused beams can exert a radiation pressure on particles near focus, [26] and the radiation force in the Rayleigh regime can be calculated according to the Rayleigh scattering theory when the radius of the trapped particle r is much smaller than the wavelength λ of the laser. In the paper, we assume spherical dielectric particles with the radius of r (r ≪ λ ) to be trapped, then the gradient force Fgrad and the scattering force Fscat can be expressed as[27]
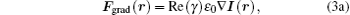 |
 |
with
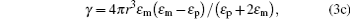 |
 |
where γ is the polarizability of the particle; ε p and ε m are the relative permittivities of the particle and the surrounding medium respectively; Cscat is the scattering cross section; 〈 S〉 is the time-averaged Poynting vector of the focused beam; ε 0 and c are the permittivity and light speed in the vacuum respectively; Re(· ) represents the real part of a complex number. With the above equations, the radiation forces on a Rayleigh dielectric microsphere produced by tightly focused ASPBs can be calculated numerically.
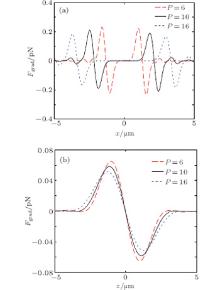
We choose the wavelength λ = 1064 nm, r = 50 nm, NA = 1.20, and the total incident power 100 mW at the pupil. Figure 4 shows the calculated gradient forces produced by tightly focused ASPBs with P = 6, 10, and 16 respectively, where the refractive index of sphere particles is 1.60, and the refractive index of the ambient is 1.33. For particles with refractive index higher than the refractive index of the ambient, multiple equilibrium points exist at focus where the particles can be trapped. The maximum transverse gradient forces are 0.232 pN, 0.210 pN, and 0.183 pN for three kinds of ASPBs with P = 6, 10, and 16, respectively, and the gradient forces decrease with the increase of the polarization orders. Meanwhile, the maximum longitudinal gradient forces are 0.0650 pN, 0.0583 pN, and 0.0513 pN respectively, and the gradient forces decrease with the increase of polarization orders. The transverse gradient forces are larger than those of longitudinal forces because of more tightly focused intensity distributions in the transverse plane. The results show multiple nanometer-sized particles can be trapped by using the focused fields of high-order ASPBs. But the number of trapped particles will be limited by the gradual decrease of gradient forces with the increase of polarization orders.
In the above sections, only the gradient force is considered, but to achieve a stable trap, the gradient force Fgrad should be larger than the scattering force Fscat, that is, R = Fgrad/Fscat > 1, where R is called the stability criterion. Here, we use R = (Fgrad)max/(Fscat)max to estimate the stability for a more conservative estimation. We calculate the R of the case (P = 10) given in Fig. 4, and it is 88.72, which verifies the feasibility of stable trapping for the trapping scheme. Another condition is that, to form a stable trap, the potential well generated by the gradient forces must be deep enough to overcome the kinetic energy of the trapping particle in Brownian motion, which generally requires
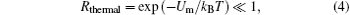
where kB is the Boltzmann constant and Um is the maximum depth of the potential well and can be calculated as | Re(γ )ε 0Imax/2| . Assuming a temperature of 300 K, we calculate Rthermal of the case (P = 10) considered in Fig. 4, and it is 3.2× 10− 12, which obviously demonstrates the stable trap in the case.
Multiple optical trapping by using high-order ASPBs is proposed, and a scheme based on far-field optical trapping is also demonstrated numerically, which confirms that multiple nanometer-sized particles with refractive index higher than the refractive index of the ambient can be trapped simultaneously. Especially, the number of trapped particles can be flexibly manipulated by changing the polarization order of ASPBs, which can be implemented by using some devices such as SLMs. The multiple optical trapping by using high-order ASPBs is expected to enhance the capabilities of traditional optical trapping systems.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|