Cite this Article
Li Hua, Zhang Shu-Lin, Qiu Yang, Zhang Yong-Sheng, Zhang Chao-Xiang, Kong Xiang-Yan, Xie Xiao-Ming. Baseline optimization of SQUID gradiometer for magnetocardiography* . Chinese Physics B, 2014, 24(2): 028501  
Permissions
Baseline optimization of SQUID gradiometer for magnetocardiography*
Li Huaa),b),c), Zhang Shu-Lina),b)†, Qiu Yanga),b),c), Zhang Yong-Shenga),b), Zhang Chao-Xianga),b), Kong Xiang-Yana),b)‡, Xie Xiao-Minga),b)
State Key Laboratory of Functional Materials for Informatics, Shanghai Institute of Microsystem and Information Technology (SIMIT), Chinese Academy of Sciences (CAS), Shanghai 200050, China
Joint Research Laboratory on Superconductivity and Bioelectronics, Collaboration Between CAS–Shanghai, Shanghai 200050, People’s Republic of China and FZJ, D-52425 Julich, Germany
University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author. E-mail: zhangsl@mail.sim.ac.cn

Corresponding author. E-mail: xykong@mail.sim.ac.cn

Project supported by the “Strategic Priority Research Program (B)” of the Chinese Academy of Sciences (Grant No. XDB04020200) and the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant No. KGCX2-EW-105).

Abstract

SQUID gradiometer techniques are widely used in noise cancellation for biomagnetic measurements. An appropriate gradiometer baseline is very important for the biomagnetic detection with high performance. By placing several magnetometers at different heights along the vertical direction, we could simultaneously obtain the synthetic gradiometers with different baselines. By using the traditional signal-to-noise ratio (SNR) as a performance index, we successfully obtain an optimal baseline for the magnetocardiography (MCG) measurement in a magnetically shielded room (MSR). Finally, we obtain an optimal baseline of 7 cm and use it for the practical MCG measurement in our MSR. The SNR about 38 dB is obtained in the recorded MCG signal.

Keyword: 85.25.Dq; 07.55.Ge; 87.55.De; 52.70.Ds; SQUID; gradiometer; baseline optimization; magnetocardiography
1. Introduction

All biomagnetic measurements face the common challenge of detecting the extremely weak biomagnetic signal from very strong environmental interference. As a magnetic sensor with very high sensitivity, a SQUID gradiometer is widely used for the biomagnetic applications, such as magnetocardiography (MCG), fetal MCG, magnetoencephalography (MEG), etc.[1– 3] A gradiometer measures the spatial difference of the magnetic field, which has substantially higher sensitivity to nearby biomagnetic sources than the distant environmental ones. Taking the first-order gradiometer for example, it is comprised of two coils wound placed in the opposite directions with a distance b in between, usually called the baseline length of the gradiometer. For the ambient noise suppression, a short baseline gradiometer is better than the longer baseline one because of the reduced sensitivity to distant sources. However, the signal amplitude of interest is also reduced to a greater extent because the compensation coil far from the sources also detects the relatively strong signal under a shorter baseline. Therefore, an appropriate gradiometer baseline is vitally important for the biomagnetic detection with high performance.

In order to optimize the gradiometer baseline, two kinds of methods were previously studied. One is pure computer simulation by using empirical parameters.[4, 5] Although effective, it is lacking in experimental validation. Therefore, in practical applications, the experimental method is widely employed. It was performed by measuring and comparing the gradiometer response repeatedly under different baselines, which was adjusted after each measurement.[6– 8] However, the environmental field changes with time. As a result, the experimental conditions may be changed with measuring time. Therefore, this method is influenced by the environmental characteristics to some extent.

In this paper, we introduce a baseline optimization method by using synthetic gradiometers. By placing several magnetometers at different heights along the vertical direction, the responses of synthetic gradiometers with different baselines can be obtained simultaneously. By using the traditional signal-to-noise ratio (SNR) as a performance index, we successfully obtain an optimal baseline for MCG measurements.

2. Baseline optimization method

Figure  1 shows the systemic measurement scheme for baseline optimization. In order to reduce the influence of the pick-up coil size, magnetometers of the same type are selected, each with a pick-up area of 10  mm× 10  mm. The signal magnetometer M0 is placed at the bottom of a dewar near the biomagnetic source. By assembling reference magnetometers Mi at different heights along the axial direction, the synthetic gradiometer can be obtained with different values of baseline bi. The synthetic gradiometer output BGi can be expressed as

where BZ0 and BZi are the outputs of M0 and Mi; BX and BY are the outputs of magnetometers along the horizontal XY direction. The orthogonality of the XY magnetometers and Mi is achieved by mechanical adjustment with a high precision. The k1, k2, and k3 are the synthesis coefficients, which are obtained by the least-square algorithm.[9] Considering the fact that the directions of M0 and Mi cannot be configured to be absolutely parallel to each other, two XY SQUID magnetometer references are added to compensate for the gradiometer imbalance.

Fig.  1. Measurement scheme for baseline optimization.

We introduce the SNR as an index to optimize the gradiometer baseline. In order to supply an MCG signal with stable amplitude, the simulated MCG signal is adopted. It is generated by a small coil driven by a simulated ECG signal through a digital-to-analog (D/A) converter, as shown in Fig.  1. The diameter of the coil is 10  mm, similar to that of one magnetic dipole. The distance between the coil and liquid helium cryostat is set to be comparable to the real MCG measurements. Figure  2 shows the definitions of the signal and noise amplitude used for SNR calculation. The signal BS is the peak-to-peak amplitude of the QRS-wave, while the noise BN is defined by the peak-to-peak amplitude of the 0.2-s section before the P-wave. Then SNR is given by

During the SNR calculation, the simulated MCG driving system may inevitably introduce extra noise. In order to eliminate the noise influence, the virtual SNR (vSNR) is also obtained for comparison based on the calculated BS using the Biot– Savart law and measured BN with the driving system off-line.

Fig.  2. Definitions of signal and noise amplitude used for SNR calculation.

By using the above methods, the optimized gradiometer baseline is obtained for the MCG measurements in an MSR.

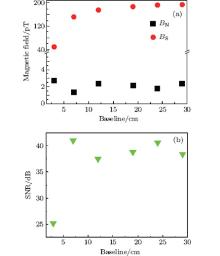
3. Measurement and simulation results

During the measurements, six axial reference magnetometers are used to obtain different baselines of 3  cm, 7  cm, 12  cm, 18  cm, 24  cm, and 28  cm. Figure  3(a) shows the measured BS and BN under different gradiometer baselines. The BS increases as the baseline lengthens and reaches a stable value after the baseline has lengthened to 24  cm. The BN appears to have some fluctuations with an average noise level of 2  pT. Based on the BS and BN, the SNR is calculated and the results are shown in Fig.  3(b). The optimal baseline with a maximum SNR is 7  cm in our MSR. Considering the fact that the performance of SQUID could be affected by environment noise, the SNR value may be different case by case; however, the tendencies of SNR under the specific application environment would be consistent.

Fig.  3. (a) Measured signal and noise (b) SNR.

Figure  4(a) gives the calculated BS and three groups of the repeatedly measured values of noise BN. With a certain distance between the coil and the cryostat, the calculated BS is unchanged. The measured BN shows a steady trend with a little difference under different baselines, which is similar to the result in Fig.  3(a). It can be concluded that the noise influence from the driving system can be ignored. Figure  4(b) shows the calculated values of vSNR under different baselines. Two of the three groups show that their optimal baselines are both 24  cm, while one is 7 cm. However, all three groups of the vSNRs at 7  cm are much more stable and repeatable than that at 24  cm. The differences may be attributed to the real-time change of the environmental fields. Although the values of BN for different baselines are different, the trends of BN are consistent. Considering the availability efficiency of helium and practical applications, the optimal baseline of 7  cm is better, which is consistent with the measurement results.

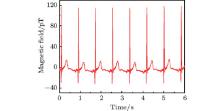
Fig.  4. (a) Calculated signal and measured noise (b) vSNR.

Based on the optimal baseline, figure  5 shows the real-time MCG signal of a volunteer. The BS is about 146  pT and the BN is about 1.8  pT. The SNR of about 38  dB is obtained. As the baseline optimization depends on the characteristics of the biomagnetic sources and environmental noises, it needs to do the optimization on a case-by-case basis.

Fig.  5. Recorded MCG signal of a 28-year old male adult.

4. Conclusion and outlook

We developed a gradiometer baseline optimization method by establishing a synthetic gradiometer system and using SNR as a performance index. An optimal baseline of 7  cm is obtained and used for the practical MCG measurement in our MSR.

As the gradiometer baseline is strongly correlated with the characteristics of the biomagnetic sources and environmental noise, this paper just gives a general solution. This method can also be applied to the baseline optimization of the higher order gradiometer and other biomagnetic measurements in shielded or unshielded environments.

Reference
1 [Cited within:1]
2 Qiu Y, Liu C, Zhang S L, Zhang G F, Wang Y L, Li H, Zeng J, Kong X Y and Xie X M 2014 Chin. Phys. B 23 088503 DOI:10.1088/1674-1056/23/8/088503 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
3 Zhang S L, Zhang G F, Wang Y L, Liu M, Li H, Qiu Y, Zeng J, Kong X Y and Xie X M 2013 Chin. Phys. B 22 128501 DOI:10.1088/1674-1056/22/12/128501 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
4 Garachtchenko A, Matlashov A, Kraus R H and Cantor R 1999 IEEE Trans. Appl. Supercond. 9 3676 DOI:10.1109/77.783826 [Cited within:1]
5 Vrba J 1997Proc. 19th Ann. Int. Conf. IEEE-EMBSChicago, IL. USA 1240 DOI:10.1109/IEMBS.1997.756592 [Cited within:1]
6 Zhang Y, Wolters N, Schubert J, Lomparski D, Banzet M, Panaitov G, Krause H J, Mück M and Braginski A I 2003 IEEE Trans. Appl. Supercond. 13 389 DOI:10.1109/TASC.2003.813864 [Cited within:1]
7 Kang C S, Yu K K, Kim K, Kwon H, Kim J M and Lee Y H 2012 Curr. Appl. Phys. 12 1319 DOI:10.1016/j.cap.2012.03.020 [Cited within:1] [JCR: 1.814]
8 Zhang Y, Wolters N, Lomparski D, Zand er W, Banzet M, Krause H J and van Leeuwen P 2003 IEEE Trans. Appl. Supercond. 13 3862 DOI:10.1109/TASC.2003.820505 [Cited within:1]
9 Zhang S L, Wang Y L, Wang H W, Jiang S Q and Xie X M 2009 Phys. Med. Biol. 54 4793 DOI:10.1088/0031-9155/54/15/010 [Cited within:1] [JCR: 2.701]