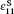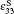The discovery of ferroelectric relaxor solid solutions (1 – x)PbMg_1/3Nb_2/3O₃– xPbTiO₃ (PMN– xPT) and (1 – x)PbZn_1/3Nb_2/3O₃– xPbTiO₃ (PZN– xPT) opened new avenues for the fundamental physical study and applications in electromechanical transducer technology.^[1] The piezoelectric properties of the crystals outperform those of the conventional PZT series piezoelectric materials, leading to a revolution in many devices in some areas, such as medicine, telecommunication and high-tech, and military industries. Their d₃₃ values are very large, ranging from 2000 Pc/n to 2500 pC/N, and the electromechanical coupling coefficient k₃₃ values are all greater than 90% .^{[1– 4]} The crystals are being studied intensively at present, owing to their excellent electromechanical properties. As is well known, a morphortropic phase boundary (MPB) is in the PZN– xPT (8% ≤ x ≤ 12% ) single crystals which exhibit the striking physical properties described above.^{[5, 6]} Many theoretical and experimental researches have been performed on the structures of PZN– xPT near the MPB by x-ray, ^[7] neutron diffraction, ^{[8, 9]} Raman scattering, ^{[10, 11]} and Brillouin scattering^{[12, 13]} in order to search for the origin of the unusual piezoelectric property of the PZN– xPT system. Despite intensive research, the PZN– xPT crystals require more systematic study since many of their properties and their structures near MPB still remain unclear.

For both fundamental study and practical applications, it is necessary to measure a complete set of matrix properties of these crystals. Such a set of elastic, piezoelectric, and dielectric constants for the 0.955PZN– 0.045PT [PZN– 4.5% PT] and the 0.92PZN– 0.08PT [PZN– 8% PT] have been reported earlier.^{[14, 15]} The measurements were carried out using a hybrid method combining ultrasonic and resonant techniques, in which the resonant frequencies of the samples were measured in the frequency range from 1 MHz to 20 MHz. However, the dielectric relaxation in a high-frequency range (50 MHz– 5 GHz) has already been found in a ferroelectric crystal. This high-frequency relaxation may also have an effect on the elastic and electromechanical properties of the ferroelectric relaxor system. Therefore, it is desirable to conduct a complete investigation of the elastic and electromechanical properties of PZN– xPT using the high frequency (10 GHz– 80 GHz) Brillouin scattering method. Brillouin spectroscopy, based on the inelastic light scattering from thermally activated acoustic phonons, measures the elastic properties of a material.^{[16, 17]} To the best of our knowledge, the determination of a complete set of elastic, piezoelectric and dielectric constants of the PZN– xPT crystal by Brillouin scattering has not been reported so far. In this paper, we present a complete set of elastic and piezoelectric constants of high-quality tetragonal poled 0.92PZN– 0.08PT single crystal grown by the modified flux method, and they are measured by high-resolution Brillouin scattering. The Brillouin spectrum consists of one longitudinal acoustic phonon mode (LA) and two transverse acoustic phonon modes (denoted as TA1 and TA2 for the low- and the high-frequency ones, respectively), and the variations of the Brillouin shifts, the full widths at half maximum, and the scattering intensities of these modes with scattering angle θ are investigated. In particular, the TA1 mode becomes markedly soft from 28.2 GHz to 18.4 GHz and broadens gradually with the increase of θ , while its intensity decreases gradually as compared with that of the original one. The possible origins of the results are discussed.

A single crystal 0.92PZN– 0.08PT selected for Brillouin scattering measurements was grown by the modified flux method.^[18] The crystal in the form of a (5 × 4 × 3 mm) cube bounded by (100), (010), and (001) faces was polished to optical clarity and the opposite faces being parallel to each other within a parallelism of ± 0.05 mm, while the error in orientation was less than 1° as determined from Laue patterns. The sample in the study was poled to use a similar method described in Ref. [13].

A Coherent C308 argon ion laser fitted with an intercavity é talon for single frequency operation at (λ = 514.5 nm) was used as an excitation source. The laser was equipped with a dedicated controller that converted any laser frequency deviation into an error signal which drove a proportional change in the laser cavity length via a piezoelectric-driven output coupler limiting the frequency jitter to less than 2 MHz over a 1-s time interval. The dispersion and detection component was a triple tandem Fabry– Pé rot interferometer manufactured by JRS Scientific Instruments.^[13] The interferometer was equipped with two dynamic vibration isolation mounts that restricted the frequency broadening due to é talon jitter to less than 1 kHz. The free spectrum range (FSR) of the interferometer is ∼ 80 GHz and the finesse of the instrument, defined as the ratio of FSR and instrumental width, was approximately 150 nm at 514.5 nm. Our measurements from Brillouin scattering were performed at room temperature.

As is well known, Brillouin scattering is based on the inelastic scattering of light by thermal phonons in a crystal and has been used to measure the sound velocity and the anisotropic velocity of sound in the crystal. The relationship between the sound velocity V_q and the Brillouin scattering frequency shift Δ ν can be determined by these scattering geometries as

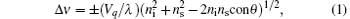
where λ is the wavelength of the exciting laser, which is 514.5 nm for the argon laser used. The n_i and n_s are refractive indices for the incident and scattered light, θ is the scattering angle, and V_q is the velocity of the longitudinal acoustic (LA) phonon mode, and the transverse acoustic (TA) phonon mode propagating with wave vector q.^[19]

Three scattering geometries of Brillouin scattering were used in the study. They are backscattering, 90° scattering, and platelet geometries. The relationship between the sound velocity V_q and the frequency shift Δ ν for these geometries can be expressed as^[19]

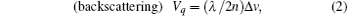
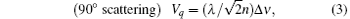
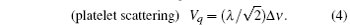
The refractive indices of 0.92PZN– 0.08PT used here were measured by the angle of minimum deviation method. The refractive index was determined to be 2.53 for a wavelength of 514.5 nm.

The equation of motion of a plane wave propagating in a piezoelectric material is^[17]

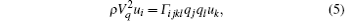
where V_q is the velocity of the acoustic phonon propagating with wave vector q; q_j (or q_l) is the projection of the unit phonon wave vector along the j-th axis; u_I and u_k are the displacement and polarization of the wave, respectively; and ρ = 8.71 g/cm³ is the density of PZN– 8% PT; Γ _ijkl is the piezoelectrically stiffened elastic modulus:^[17]

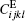
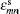
Here, is the elastic stiffness modulus in a constant electric field, e_rij and e_skl are both the piezoelectric stress constants, and is the permittivity at constant strain, whereas l_m and l_n are the directional cosines of the wave propagation direction. 0.92PZN– 0.08PT is the tetragonal phase, belonging to the space group 4-mm symmetry. There are a total of 11 independent physical constants describing the elasto– piezo– dielectric matrices for this symmetry. Hence, there are six elastic constants , three piezoelectric constants (e_mi, mi = 15, 31, 33), and two dielectric constants (ε _mn, mn = 11, 33). The wave propagation equations along the [100], [001], and [110] directions for three scattering geometries used in 4-mm symmetry to determine these eleven independent parameters have been reported early.^[13]

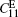
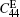
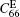
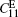
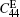
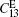
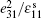
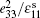
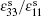
From the theoretical prediction, it is evident that the ρ V² values can be determined by Brillouin scattering in different geometric configurations. By using the measured values, four elastic constants, , , , and , and one ratio of the square of piezoelectric constant to permittivity, , can be directly determined as indicated in the wave propagation equations.^[13] The uncertainties in , , are less than 3% , and in it is about 5% . The which may be calculated from either Eq. (A4a) or Eq. (A4c) in the equations, ^[13] carries an estimated error of about 5% . The remaining data are derived to use velocities with the (010) plane by Brillouin scattering in the platelet geometry. A total of forty sets of velocity measurements are performed for the LA and TA phonon modes in fifteen directions. The elastic constants, and , the ratios of the square of piezoelectric constant to permittivity, and , and the ratio of permittivities, , are derived using the equations listed in Ref. [13]. A combining algebraic computations with a computer-based nonlinear least-squares fitting method are employed in the study. The quality of the fitted results and measured values are illustrated in Fig. 1. The solid lines and solid circles in Fig. 1 represent the computational and experimental values for different modes, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Vq values (m· s− 1) from Brillouin scattering for the longitudinal and two transverse acoustic phonon modes in the (001) plane of tetragonal 0.92PZN– 0.08PT. The solid curves and the solid circles represent the computer-generated fittings to the data and measured values, respectively.

Figure 1 shows the angular dependences of V_q for the quasi-longitudinal acoustic phonon mode (QLA) and the two transverse acoustic phonon modes (TA1 and TA2) , propagating in the (001) plane. The LA mode is a quasi-longitudinal wave propagating in the (001) plane, and its displacement vector is in the same plane, but the displacement vector is parallel to the direction of propagation only in the highly symmetric [100] and [010] directions. For TA2 mode, it is a pure shear wave having a direction of propagation in the (001) plane and a displacement vector perpendicular to that plane. Hence, the angular dependence ofV_q on modes of different propagation directions is isotropic in the (001) plane. However, for the TA1 mode, the angular dependence of V_q on modes of different propagation directions shows a stronger anisotropy, because it is a quasi-shear wave with displacement vector in the (001) plane but perpendicular to the direction of propagation only in the high symmetry [100] and [010] directions. It can be seen from Fig.1 that the fitted results are in good agreement with the experimental values. By considering the experimental and computational errors, the uncertainties in and are both about 4% , while those in , , and are all below 5% . From the velocity of sound, measured by the Brillouin scattering, a complete set of elastic, piezoelectric, and dielectric constants are determined and presented in Table 1. For comparison with previous theoretical and experimental data, ^[15] check Table 1. It can be seen from Table 1 that the data in the study are in agreement with those measured previously by a hybrid method combining ultrasonic and resonant techniques.^[15] However, it is suggested that high-frequency relaxation cannot exert an influence on the measurements of those parameters, obviously.

Table 1.

Table 1.

Table 1. Elastic, piezoelectric, and dielectric constants of tetragonal 0.92PZN– 0.08PT. Elastic stiffiness moduli/GPa 118.7 ± 3 % 108.2 ± 2 % 105.1 ± 4 % 107.4 ± 5 % 62.5 ± 3 % 66.4 ± 3 % (115)a (105) (102) (101) (64) (63) Piezoelectric stress constant: e/(C/m2) e15 e31 e33 11.07 (10.1) – 5.81 (– 5.1) 16.1 (15.4) Dielectric constants: ε 2680 (2720) c967 (984) a The values in the parentheses are obtained by using ultrasonic techniques.[15]

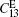
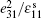
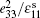
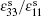
Table 1. Elastic, piezoelectric, and dielectric constants of tetragonal 0.92PZN– 0.08PT.

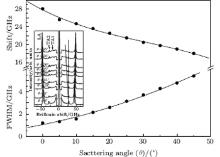
For all measured curves, each Brillouin spectrum consists of one LA and two TA modes (denoted as TA1 and TA2 for the low- and the high-frequency ones, respectively). Figure 2 shows angular dependences of frequency shift (top) and full width at half maximum (FWHM, bottom) of the TA1 mode obtained from Brillouin scattering. The intensities, positions, and FWHMs of three acoustic modes are plotted in the inset of Fig. 2 each as a function of scattering angle θ . It can be seen from Fig. 2 that the intensity of the LA mode increases and their positions shift toward larger frequency gradually as scattering angle θ increases. The value of the Brillouin shift for the LA mode reaches a maximum value of 47.8 GHz in the [110] direction. On the other hand, the Brillouin shift of the TA2 mode does not change at all for different propagations, because it is a pure shear wave which has a direction of propagation in the (001) plane and displacement vector perpendicular to the plane. Among the observed spectra, the most striking feature of the present study is that the peak intensity, peak position, and FWHM of the TA1 mode vary drastically with scattering angle θ , compared with those of the LA and TA2 modes. From Figs. 1 and 2, we can see that the peak position of the TA1 mode shifts monotonically from 28.2 GHz to 18.4 GHz with the increase of the scattering angle θ from 0° to 45° . The change in the frequency shift manifests that the velocity of the TA1 mode reaches a minimum in the [110] direction. Therefore, V_[110] for the TA1 mode, which propagates along (110) and is polarized along (001), seems to act as a “ soft transverse acoustic mode” in 0.92PZN– 0.08PT. The TA1 mode decreases in intensity and broadens gradually with increasing the scattering angle θ compared with that of the original one. The FWHM values of the TA1 modes increase from 1.2 GHz to 5.4 GHz as scattering angle θ increases from 0° to 45° . The variations in the intensity, position, and FWHM of the TA1 mode with scattering angle θ may be associated with the strong anisotropic piezoelectric interaction present in the poled 0.92PMN-0.08PT. These results provide useful information for studying the relationship between the microheterogeneity and the complete set of matrix properties in the ferroelectric relaxor crystals. However, further investigation is necessary to confirm the suggestion.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Angular dependences of frequency shift (top) and FWHM (bottom) of the TA1 mode, obtained from Brillouin scattering. The solid curves and the solid circles are the computer-generated fittings to the data and measured values, respectively. The inset shows the typical Brillouin spectra from the (001) plane of 0.92 PZN– 0.08PT single crystal.