For the last couple of decades, strongly correlated physics has attracted considerable attention. Due to various interdot and intradot interactions, the coupled multi-quantum dots system has been considered as a versatile tool for studying strongly correlated behaviors, such as the Coulomb-blockade effect, the Fano effect, the Kondo effect, and the quantum phase transition (QPT).^{[1– 20]} Basically, these quantum effects depend closely on the configurations of the dots and the leads, and also the interactions that have been employed. Recently, triple quantum dots (TQD) have been fabricated and realized in semiconductor heterostructures and self-assembled systems.^{[21– 28]} Theoretically, much attention has been paid to the QPT and transport property in TQD systems. For instance, in a serially coupled TQD including one intermediate dot and two peripheral dots, the equilibrium and nonequilibrium Kondo transport properties were studied.^{[29, 30]} When the three dots are identical, the transition between local-moment and molecular-orbital is visible when the interdot tunnel coupling increases.^[31] For a parallel TQD system with one central dot and two side dots, the ferromagnetic Kondo effect is studied, ^[32] and the spin correlation between two side dots can be ferromagnetic or antiferromagnetic, depending on the charge of the central dot.^[33] When three dots are coupled symmetrically to two leads, there exist two first-order QPTs due to the competition between the interdot tunnel coupling and the Ruderman– Kittel– Kasuya– Yosida (RKKY) exchange interaction, ^[34] and the conductance is discontinuous through the quantum phase transitions.^[35] For a triangular TQD with only one dot connected to the leads, the QPT and Kondo effect are studied in impurity trimers.^{[36, 37]} When the TQD are pierced by an external magnetic flux, the Kosterlitz– Thouless (KT) transition induced by the Aharonov– Bohm effect has been explained by the three-order superexchange interaction.^[38] For triangular TQD with two channels, the Kondo phases and frustration-induced transitions are studied.^[39] For triangular TQD connected to two non-interacting leads, the low-energy properties and characteristic Kondo energy scale are studied in a wide parameter range of the gate voltage.^{[40, 41]}

Recently, the importance of the interdot capacitive coupling has been demonstrated in some TQD systems. For instance, for an isolated triangular TQD system, the electronic structure and charging diagram have been studied using the Hubbard model and real-space exact diagonalization techniques.^[22] For a triangular TQD with two channels, the interplay between Aharonov– Bohm current oscillations, coherent electron trapping and spin blockade have been discussed.^[42] When the TQD is connected to two sources and one drain, the dark state in the transport has also been revealed.^[43] For a triangular molecule placed in an electric field, the effect of the field is shown to be anisotropic, and include both linear and nonlinear parts.^[44] For a TQD system including the on-site Coulomb repulsion, the interdot capacitive coupling and also the external magnetic field, the QPT and electronic transport are studied for a wide range of the gate voltage.^[45] For a spinless triangular TQD system, the charge oscillation has been explained by the many-body effect.^[46]

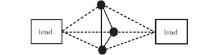
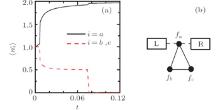
Although both the interdot tunnel coupling (interdot hopping) t and the interdot capacitive coupling (interdot Coulomb repulsion) V play important roles in the QPT and transport property in TQD systems, little is known about their interplay in these features. In this paper, we consider a triangular TQD including both V and t (see Fig. 1), and discuss the QPT and transport property under different conditions. When t = 0, due to the strong interdot capacitive coupling V, one of the dots is doubly occupied, one dot is singly occupied, and the remaining one is empty for the case of particle– hole (p– h) symmetry. With increasing t, there exist two first-order transitions between local spin doublet, magnetic frustration phase, and orbital spin singlet due to the competition between V and t. For small t, the conductance reaches to the unitary limit according to the Coulomb-blockade effect. As t is large enough, the conductance is strongly suppressed for the bonding state is doubly occupied. When t is absent, the evolutions of the total charge on the dots and the linear conductance are typical of the Coulomb-blockade features as the gate voltage increases. While for sufficient t, the antiferromagnetic spin correlation between dots is enhanced, and the conductance is strongly suppressed.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic view of the triangular TQD setup attached to the conduction leads.

The rest of the paper is organized as follows. In Section 2, we define the model Hamiltonian of the TQD system, and present the calculation algorithms and formulations. In Section 3, we discuss the quantum phase transition and the transport property of the system. Finally a summary is given in Section 4.

The triangular TQD system in Fig. 1 is described by the following Hamiltonian

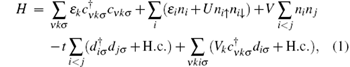
where annihilates (creates) a spin-σ electron of wave vector k and energy ε _k in lead ν (ν = L, R). annihilates (creates) a spin-σ electron of energy ε _i in dot i (i = 1, 2, 3), is the number operator of spin-σ for the i-th dot, and n_i= n_i↑ + n_i↓ is the number operator for site i. U is the on-site Coulomb repulsion, V is the interdot capacitive coupling and t is the tunnel coupling between dots. V_k is the tunnel matrix between two leads and three dots, and we assume V_k is symmetric with respect to the dots and the leads.

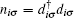
We solve this model by employing the Wilson’ s numerical renormalization group (NRG) method, ^{[47– 49]} which is a nonperturbative technique for treating quantum impurity problems. In our NRG treatment, the discretization parameter Λ , which characterizes the logarithmic discretization of the conduction band, is set to be 2.0, and the number of the many-body states kept at each iteration is 2000. We assume a constant density of state ρ ₀ for the conduction band of the leads and a dispersionless conduction band with bandwidth 2D, so the hybridization function Γ = 2π ρ ₀Σ _k| V_k| ² between quantum dots and conduction leads also turns out to be a constant. The conductance through the dots is calculated using the Landauer formula, ^[50]

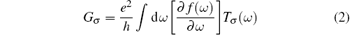
with the Fermi function f(ω ) and the transmission coefficient

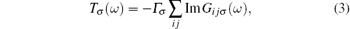
here, the retarded dot Green function is defined as . In the calculations of electronic transport, a different procedure with respect to the reduced density matrix of the full system is applied, ^[51] which has been proved to improve the accuracy of the spectral density. In the following, the Fermi energy is chosen as ε _kF = 0, then the linear conductance at zero temperature in the limit of zero bias is determined by

The charge of the dots n is defined by

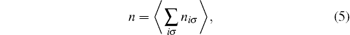
the double occupation of each dot and the spin correlation between dots i and j are given by ⟨ n_iun_id⟩ and ⟨ S_iS_j⟩ respectively, where S_i is the total spin operator of the i-th dot and u = ↑ , d = ↓ .

In this section, we discuss the effects of interdot capacitive (V) and tunnel (t) couplings on the QPT and the transport property of the triangular quantum dots. We concentrate on the strongly correlated regime described by U/Γ ≫ 1 and/or V/Γ ≫ 1. The half bandwidth of the leads D is chosen as the energy unit. In the U-dominated regime, the interplay between U and t in triple dot structures has been well elucidated.^{[19, 34]} Therefore, in order to make a clear understanding of the interplay between V and t, and compare with previous works, we fix U = 0.1, V = 0.15, and Γ = 0.01 throughout this paper. Note that we have assumed V > U here, which means that the three spatially separated quantum dots are not too small, and may have the stronger capacitance couplings to each other. These conditions have been achieved in experiment (see Ref. [52]). For the sake of simplicity, we consider that the three dos are identical, namely ε _i = ε , which can be tuned experimentally by the external gate voltage.

Firstly, we fix ε = − U/2 − 2V, thus ε satisfies the p– h symmetry when t = 0. Figures 2(a) and 2(b) present the total charge of three dots n, the double occupation of each dot ⟨ n_iun_id ⟩ , and the spin correlation ⟨ S_iS_j⟩ between dots i and j as functions of t at zero temperature. When t = 0, the TQD is half-filled according to the p– h symmetry, namely, the total charge of the dots n = 3. Due to the strong V, which favors each dot being doubly occupied, the many-body state (n₁n₂n₃) is more likely to have the configuration of (210) (or (201), (102), (120), (021), (012)), in which one dot is doubly occupied, one dot is singly occupied, while the remaining one is empty. (For three dots are equivalent by symmetry, each dot may be doubly occupied, singly occupied, or zero occupied in an equal possibility). Thus the spin correlation ⟨ S_iS_j⟩ ≈ 0 and the TQD forms a local spin doublet. The double occupation of each dot ⟨ n_iun_id⟩ ≈ 0.37 is a little bigger than 1/3, which is valid in the limit of V → ∞ (or U → 0), because in our work a finite V/U is employed. When t > 0, the p– h symmetry is damaged.^{[47, 48]} The charge on the dots n grows with increasing t, therefore, the probability of double occupancy on each dot increases. In this process, the interdot capacitive coupling V competes with the interdot tunnel coupling t, which favor different spin configurations in the many-body state, so that there are discontinuous changes in n, ⟨ n_iun_id⟩ , and ⟨ S_iS_j⟩ at t = t_c1 = 0.0068. When t > t_c1, n ≈ 3, ⟨ n_iun_id⟩ ≈ 0.23, and ⟨ S_iS_j⟩ ≈ − 0.05, indicating that in this phase there are several equally probable ways for the electron spin ordering. Therefore, the ground state of the TQD is a magnetic-frustration phase. As t grows to another critical point t_c2= 0.0757, n drops to about 2, ⟨ n_iun_id⟩ and ⟨ S_iS_j⟩ decrease rapidly to 0.12 and − 0.15 respectively. The abrupt changes in these functions indicate that the QPTs at t_c1 and t_c2 are of the first order. In order to get a better understanding of the ground state in these phases, we define the bonding state and the antibonding states and . Under this transformation, only the bonding state hybridizes with the conduction band, while the antibonding states seem like quasi-localized states.^{[34, 35, 45, 53]} Therefore, the parallel triangular TQD system is completely equivalent to the model shown in Fig. 3(b). In Fig. 3(a), we present the charge occupation of orbit f_i (i = a, b, c) as functions of t, where and . When t_c1 < t < t_c2, one finds and , indicating orbit f_a is almost doubly occupied, and orbit f_b (or f_c) is singly occupied. When t > t_c2, , while drops to 0. In this case, the present model maps to the single impurity Anderson model with f_a coupling to the conduction leads, thus the ground state is an orbital spin-singlet. To estimate the value of the critical points t_c1 and t_c2, one may change the present model to an effective Kondo model according to Schrieffer– Wolff– type transformation.^[54]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Total charge of three dots n, (b) double occupation of each dot ⟨ niunid⟩ (u = ↑ , d = ↓ ) and spin correlation between dots i and j ⟨ SiSj⟩ as functions of interdot tunnel coupling t at zero temperature. Here, Γ = 0.01, U = 0.1, V = 0.15, and ε = − U/2– 2V.

Fig. 3.

	Figure Option ViewDownloadNew Window
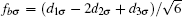
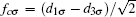
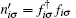
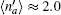
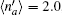
	Fig. 3. (a) Charge occupation of the transformed orbits fi(i = a, b, c) as functions of t, (b) schematic model described by fi. The remaining parameters are the same as those in Fig. 2.

Next, we study the electronic transport though the TQD. Panels (a) and (b) in Fig. 4 show the transmission coefficient T(ω ) at zero temperature for various t. For t = 0, T(ω = 0) reaches to the unitary limit, corresponding to full conductance G = 2e²/h. However, the peak at ω = 0 does not relate to the Kondo effect, and can be explained by the usual Coulomb-blockade effect. To make a clear understanding of the underlying physical picture, we present T(ω ) in the limit of V = 0.15, and U = t = 0 in Fig. 4(a). One may find that even for U = 0 we still get a perfect conductance with G approaching 1.0. For U = 0 and ε at the p– h symmetric point ε = − 2V, the TQD is also in the local doublet as discussed above. Adding an additional electron to the singly occupied dot will cost energy ε + 2V = 0, which is equal to the Fermi level. Thus, the electron can transmit the TQD freely. Similar behaviors have also been found in other literature.^{[45, 55, 56]} With increasing t, the spectral of T(ω ) moves to the left. When t increases to t > t_c1, the transmission coefficient T(ω = 0) is strongly suppressed. When t is large enough (e.g., t = 0.02 and 0.08), T(ω = 0) ≈ 0, corresponding to zero conductance. According to Eq. (3) and the schematic model in Fig. 3(b), T(ω ) is merely determined by the density states of the bonding state f_a. When t > t_c1, orbit f_a is almost doubly occupied, thus the electron cannot transmit the dots.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Transmission coefficient T(ω ) at zero temperature for U = 0.1, t = 0.0 (solid line), U = 0.1, t = 0.0065 (dashed line), and U = 0.0, t = 0.0 (dotted line); (b) T(ω ) for U = 0.1 and various t. The other parameters are given by Γ = 0.01, V = 0.15, and ε = − U/2– 2V.

Figure 5(a) shows the total charge of the TQD n as a function of charge energy ε for different t. One finds that n increases in a steplike manner with decreasing ε . However, the behaviors of n are quite different with respect to various t. For example, when t = 0, there are platforms in the regimes of even n, while for large t (e.g., t= 0.08), n nearly does not change in segments n = integer (n ≥ 2), and abrupt jumps are observed at some particular gate voltage. To understand these behaviors, one may analyze the energy scale of the isolated TQD model as discussed in the following. In the case of t = 0, three dots start to be occupied as ε decreases to approaching the Fermi level. When ε < − 0.15, the total charge on the dots is about n = 2. In order to reduce the total energy, the many-body state (n₁n₂n₃) is more likely to have the configuration (200) (or (020), (002)), in which one of the dots is doubly occupied, while the other two dots are empty. In this case, the total energy of the system is about V– U less than the state with the configuration (110) (or (101), (011)), where two dots are singly occupied while the remaining one is empty. As ε decreases further, to add an additional electron on the TQD will cost energy ε + 2V, which is much higher than the Fermi energy. Therefore, n nearly does not change and the double occupation ⟨ n_iun_id⟩ ≈ 1/3 holds in segment − 0.25 ≤ ε ≤ − 0.15 (see Figs. 5(a) and 5(b)). When ε < − 0.25, ε + 2V approaches to the Fermi level, hence n increases again. When ε < − 0.45, the total charge is about n = 4, similar to the case of n = 2, (n₁n₂n₃) favors the configuration of (220) (or (202), (022)), where two dots are doubly occupied while the remaining one is empty. As ε decreases continuously, the total charge of the TQD nearly does not change and the double occupation ⟨ n_iun_id⟩ ≈ 2/3 holds, because to add an additional electron on the many-body state of (220) will cost energy ε + 4V. When ε < − 0.75, the charge on the dots is nearly n = 6, thus three dots are doubly occupied, and ⟨ n_iun_id⟩ ≈ 1. In Fig. 5(c), the local spin correlation ⟨ S_iS_j⟩ is plotted as a function of ε for various t. When t = 0, we find that ⟨ S_iS_j⟩ = 0 in the regimes of even n, because in these regimes, some dots are doubly occupied, and the remaining are/is empty, e.g., the many-body state is dominated by (200) (or (020), (002)) when n = 2. While in the regimes of odd n, the local spin correlation shows a slightly antiferromagnetic coupling. Similar behaviors have also been found in Ref. [35] for the N-QD system (N ≥ 2) without interdot capacitive coupling and in Ref. [53] for the DQD model with V < U. Compared to the results of Ref. [35] and Ref. [53], we find that the AFM phases in the present model can be understood in a similar way. Take n = 3 for example, in this regime, one of the dots is doubly occupied, then the remaining dots map to the 2-QD system (DQD model) with one electron, thus the AFM can be observed. For the case of t ≠ 0, the dots start to be occupied at a higher gate voltage and the platforms of odd n are found, e.g., when t = 0.08, n changes from n = 0 to 2 more quickly compared to t = 0 (see Fig. 5(a)). This is due to the following fact: although adding an additional electron on n = 1 will increase the interdot capacitive interaction, the negative tunnel coupling will compensate it. According to Fig. 5(c), one may also find that the AFM coupling in the local spin correlation is enhanced with increasing t, for the interdot tunnel coupling favors antiparallel spin configuration between dots in the many-body state. In the segments of odd n (n ≥ 3), adding an additional electron on the TQD not only needs to overcome the effect of V and/or U, but may also weaken the effect of t, thus the platforms of odd n can be observed in Fig. 5(a).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) Total charge of three dots n, (b) double occupation of each dot ⟨ niunid⟩ and (c) spin correlation between dots i and j ⟨ SiSj⟩ as functions of charge energy ε for t = 0 (solid line), t = 0.01 (dashed line), and t = 0.08 (dotted line). The remaining parameters are give by Γ = 0.01, U = 0.1, and V = 0.15.

In Fig. 6(a), we depict the linear conductance G at zero temperature versus charge energy ε for various t. When t = 0, G shows a symmetric line shape with respect to the p– h symmetric point ε = − 0.35. One may find that in the regimes of odd charge occupation, G approaches to the unitary limit G = 2e²/h, while in the regimes of even n, G is nearly 0. This is the typical feature in the Coulomb-blockade effect and satisfies the Friedel Sum Rule.^{[57, 58]} In the presence of sufficient t, some asymmetric peaks develop. In Fig. 6(b), we present the charge occupation of the transformed orbits f_i as functions of ε for t = 0.01. We find that the peaks in G corresponding to close to 1, and the valleys corresponding to close to 2 (or 0). For large t (e.g., t = 0.08), the peaks are strongly suppressed for n ≥ 2, which could also be understood according to the evolutions of the charge occupations on the changed orbits . As shown in Fig. 6(c), when n ≥ 2, orbit f_a is almost doubly occupied, thus the linear conductance G ≈ 0.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (a) The linear conductance G as a function of charge energy ε for t = 0 (solid line), t = 0.01 (dashed line), and t = 0.08 (dotted line). (b) and (c) Charge occupation of the transformed orbits fi (i = a, b, c) as functions of ε for t = 0.01 (panel (b)) and t = 0.08 (panel (c)). Here, the remaining parameters are the same as those in Fig. 5.

In this paper, we study the quantum phase transition and the transport property of a triangular TQD system in the strongly correlated regime. The interdot– capacitive coupling V favors each dot being doubly occupied, while the interdot tunnel coupling t favors the antiparallel spin configuration. We concentrate on their interplay in the electronic transport and the QPT, and obtain a rich range of physical behaviors. With fixed ε = − U/2 − 2V, there exist two first-order transitions between local spin doublet, magnetic-frustration phase, and orbital spin-singlet due to the competition between V and t. For small t, the conductance reaches to the unitary limit according to the Coulomb-blockade effect. For large t, the conductance is strongly suppressed for the bonding state is doubly occupied. By tuning the gate voltage ε , the evolutions of the total charge on the TQD and the linear conductance are of the typical Coulomb-blockade features when t = 0. With increasing t, the antiferromagnetic spin correlation between dots is enhanced, and the conductance is suppressed, which can be understood through the evolutions of the charge occupations on the bonding state and antibonding states. We believe that our work not only clarifies the interplay between the interdot-capacitive coupling and the interdot tunnel coupling in a triple dot structure, but may also provide guidelines for both theoretical and experimental studies of these ideas in the future.