Cite this Article
Wang Zhan-Yu, Zhou Yan-Li, Wang Xue-Qing, Wang Fei, Sun Qiang, Guo Zheng-Xiao, Jia Yu. Effects of in-plane stiffness and charge transfer on thermal expansion of monolayer transition metal dichalcogenide* . Chinese Physics B, 2014, 24(2): 026501  
Permissions
Effects of in-plane stiffness and charge transfer on thermal expansion of monolayer transition metal dichalcogenide*
Wang Zhan-Yua),b), Zhou Yan-Lic), Wang Xue-Qingb), Wang Feia),b), Sun Qianga),b), Guo Zheng-Xiaoa),b),d), Jia Yua),b)†
International Joint Research Laboratory for Quantum Functional Materials of Henan, Zhengzhou University, Zhengzhou 450001, China
School of Physics and Engineering, Zhengzhou University, Zhengzhou 450001, China
Department of Mechanical and Electrical Engineering, Henan Industry and Trade Vocational College, Zhengzhou 451191, China
Department of Chemistry, University College London, London WC1H 0AJ, U.K.

Corresponding author. E-mail: jiayu@zzu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11274280 and 11104254) and the National Basic Research Program of China (Grant No. 2012CB921300).

Abstract

The temperature dependence of lattice constants is studied by using first-principles calculations to determine the effects of in-plane stiffness and charge transfer on the thermal expansions of monolayer semiconducting transition metal dichalcogenides. Unlike the corresponding bulk material, our simulations show that monolayer MX2 ( M = Mo and W; X = S, Se, and Te) exhibits a negative thermal expansion at low temperatures, induced by the bending modes. The transition from contraction to expansion at higher temperatures is observed. Interestingly, the thermal expansion can be tailored regularly by alteration of the M or X atom. Detailed analysis shows that the positive thermal expansion coefficient is determined mainly by the in-plane stiffness, which can be expressed by a simple relationship. Essentially the regularity of this change can be attributed to the difference in charge transfer between the different elements. These findings should be applicable to other two-dimensional systems.

Keyword: 65.80.–g; 63.22.Np; transition metal dichalcogenide; thermal expansion; phonon
1. Introduction

Understanding the thermal and structural properties of two-dimensional (2D) systems is one of the most important and fundamental issues in science with a wide spectrum of applications.[1] In the quasi-harmonic approximation (QHA), the thermal expansion coefficient[2] for a three-dimensional (3D) crystal is equal to (1/BV)∑ q, jΓ q, jcυ q, j(T) (where B is the bulk modulus, V is the unit cell volume, Γ q, j ( = − ∂ ln ω q, j ∂ ln V) is the Grü neisen parameter of the vibrational state with frequency ω q, j, and cυ q, j(T) is the specific heat). Therefore, the volumetric thermal expansion varies inversely with the bulk modulus. However, for a 2D monolayer structure, the thickness becomes ambiguous. The in-plane stiffness is regarded as a more suitable measure of the rigidity rather than the bulk modulus.[3– 5] Owing to sharing the same hexagonal lattice, the monolayer semiconducting transition metal dichalcogenide (STMD) is an ideal prototype to determine the correlation between thermal expansion and in-plane stiffness.

The STMD is gaining increasing attention and offers an opportunity for fundamental and technological research in a variety of fields including catalysis, energy storage, sensing, and electronic devices such as field-effect transistors and logic circuits.[6– 14] For instance, monolayer MoS2, a prototypical example of STMD with a large intrinsic direct bandgap of ∼ 1.8 eV, [15] is a very desirable candidate for optoelectronics and digital electronics with thermal stability up to 1100.[9, 16, 17] However, the performance of the complex MX2-based devices will change significantly due to internal stresses imposed by different expansion coefficients. Thus it is important to determine the thermal expansion coefficient as a function of temperature.[18– 21] In addition, according to the ubiquitous membrane effect, [22, 23] the ZA bending acoustic modes may cause negative thermal expansion in membranes or layered materials. In particular, many studies on graphene, graphite, and boron nitride have directly manifested this phenomenon.[24] Thus, the monolayer STMD is also expected to contract at some specific temperatures.

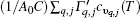
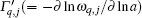
In this article, first-principles phonon calculations are used to determine how the lattice constant of monolayer MX2 changes with the increase of temperature. Unlike the corresponding bulk material, [25] monolayer MX2 shows a negative thermal expansion (NTE) at low temperatures. The positive linear thermal expansion coefficient of a 2D system can be written as , where C is the in-plane stiffness, A0 is the equilibrium area for the single layer, and is the mode Grü neisen parameter. Thus, the thermal expansion of a 2D system shows the inverse correlation with the in-plane stiffness C. Furthermore, our calculated results show that the difference in their in-plane stiffness can be attributed to the difference in charge transfer.

2. Computational details

The static lattice energy and the Hellmann– Feynman force are calculated using the density-functional theory (DFT), implemented in the Vienna ab initio simulation package (VASP).[26– 28] The projector-augmented wave function (PAW) method[29] with the Perdew– Burke– Ernzerh[30] (PBE) of generalized gradient approximation (GGA) is adopted. A large spacing of ∼ 15 Å between 2D single layers of MX2 is taken to prevent interlayer interactions. The plane-wave energy cutoffs are 470 eV (WS2), 400 eV (MoS2, WSe2, and WTe2), and 380 eV (MoSe2 and MoTe2). The Brillouin-zone (BZ) is sampled by a 10× 10× 1 Gamma centered k mesh for the primitive MX2 unit cell. The total energy is calculated with high precision, and converges to 10− 8 eV/atom. And the lattice constants and the atom coordinates are optimized until the interatomic force is less than 10− 6 eV/Å .

The phonon calculations are performed by using the supercell method through the PHONOPY code, [31] and the real-space force constants of supercells are calculated by using the density-functional perturbation theory (DFPT) as implemented in VASP. In our calculations, the nonanalytic contribution to the dynamical matrix in the limit q→ 0 is even smaller and is neglected. Then the thermal expansion of MX2 can be calculated by the phonon dispersions based on the QHA. Within the QHA, Helmholtz free energy F(T, {ai}) with respect to all the geometrical degrees of freedom {ai} in a crystal is expressed as[32, 33]

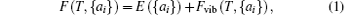
where E({ai}) is the total energy of the solid when all atoms are fixed at their crystalline lattice sites, and the second term on the right-hand side is the vibrational contribution to the Helmholtz free energy, which can be calculated using the relationship[34]

where ω q, j({ai}) indicates the dependence of the phonon frequency on the structural parameters {ai}. For our QHA calculations, necessary routine numerical checks on the reliability of the supercell size are made and supercells containing 4× 4× 1 primitive cells are chosen for all STMDs. Direct minimization of the free energy F(T, {ai}) provides the corresponding equilibrium structure at temperature T and zero pressure. So their linear thermal expansions are easily obtained as a variation in the equilibrium lattice constants.

According to Grü neisen theory, the linear thermal expansion coefficient for monolayer MX2 can be given by[24]

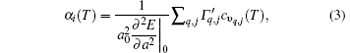
where the subscript “ 0” indicates a quantity taken at the ground state lattice parameter. Since cυ q, j(T) is always positive, it is clear that the negative thermal expansion results only from negative values of the Grü neisen parameters for certain phonons. Note that the term 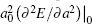in Eq. (3) is equal to 9V0B0 for 3D isotropic crystalline solid.

3. Results and discussion
3.1. In-plane stiffness and charge transfer

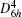
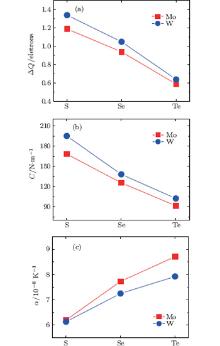
The crystal structure of 2H– MX2 belongs to the point group (space group P63/mmc), and the unit cell consists of six atoms.[35] In contrast, monolayer MX2 belongs to the space group P6m2. The M and X atoms form a hexagonal lattice with trigonal prismatic coordination as depicted in Fig. 1. The calculated structural parameters are listed in Table 1. The data show that the lattice constants of MX2 monolayers of the same X atoms, which are nearly identical, and other lattice parameters, such as the bond angles, change slightly. For MoX2 or WX2, the structural parameters including lattice constants increase significantly with increasing the X atomic radius. Experimental data of the lattice parameters of monolayer STMD are not available yet. However, our calculated lattice constants are close to those of their bulk counterparts. For example, the optimized lattice constant of the MoS2 is 3.19 Å , which is almost the same as the experimental value (3.16 Å )[36] of 2H– MoS2.

Fig. 1. (a) Top and (b) side views of the atomic structure of monolayer MX2. The figure shows a 4× 4 supercell, and the primitive unit cell with lattice vectors a and b (| a| = | b| ) is highlighted by a parallelogram. The relevant internal structural parameters are also indicated. (c) Corresponding Brillouin zone with some high-symmetry points.

For the single layer MX2, the in-plane stiffness C mentioned above can be given as[37] 1/A0(∂ 2ES/∂ ε 2), where ES is the strain energy calculated by subtracting the total energy at zero strain from the total energy at a given strain (ES = Eε − Eε = 0), and ε is the in-plane uniaxial strain (ε = Δ a/a). In Table 1, in-plane stiffness and the charge transfers of metals for these monolayer semiconductors are also presented. Using the Bader analysis, [38] the charge transfer from the metal to the chalcogen atom is obtained. For MoX2 or WX2, the charge transfer decreases with increasing the row number of the X atom. Generally, the higher the charge transfer, the larger the in-plane stiffness is. Thus the in-plane stiffness decreases with increasing the row number of X. Moreover, the in-plane stiffness of WX2 is usually higher than those of MoX2.

Table 1. Calculated values of lattice constant a, bond lengths (dM− X and dX − X), X– M– X bond angle θ , in-plane stiffness C, and charge transfer of metal Δ Q for monolayer STMD.
3.2. Phonon

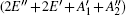
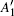
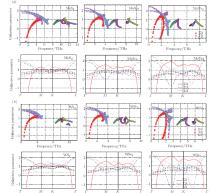
Phonons play a crucial role in determining the thermodynamic properties of crystal. Before determining the thermal expansion of monolayer STMD, it is imperative to investigate their vibrational properties systematically. Since monolayer MX2 has three atoms per primitive cell and is given by point group D3h, besides three acoustic modes, six optical modes at the BZ center are therefore expected. Several studies on their vibrational properties have been reported. For example, Najmaei et al.[39] examined the temperature dependences of the MoS2 vibrational modes with thickness values ranging from a single layer to a few layers. They demonstrated that thermal expansion plays a significant role in determining the temperature dependence of the out-of-plane mode A1g, corresponding to the mode of the monolayer MoS2.

Figure 2 shows the calculated phonon dispersion curves for monolayer MX2 along the high-symmetry points in the first BZ. The calculated acoustical and optical branches of monolayer STMD are positive for any point in BZ, indicating that these suspended, monolayer MX2 compounds are stable. As a characteristic feature of the phonon dispersion of layered crystals, the out-of-plane acoustical (ZA) mode of monolayer MX2 displays a parabolic dispersion because the transverse force decays exponentially, in contrast to the in-plane longitudinal acoustic (LA) and transverse acoustic (TA) branches showing linear dispersions near the Γ point. From Fig. 2, it is clear that the widths of the acoustical and optical branches of MoX2 or WX2 decrease with increasing the row number of the X atom. This is mainly because the strength of the M– X bond reduces as the mass of the X atom increases.

Fig. 2. Ab initio calculations of phonon dispersion curves along the Γ – M– K– Γ direction of the BZ, and vibrational density of states (DOS) for monolayer MX2 at the equilibrium volume. All branches are presented with sharing the same scale of frequency. All acoustical modes (ZA, TA, and LA) as well as vibrational DOS are shown using the same graph legend.

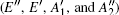
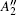
In order to understand clearly their vibrational properties, the frequencies and the corresponding atomic displacements of the optical modes ( at the Γ point are plotted in Fig. 3. For E″ and modes, which are associated with the motions of chalcogen atoms, the vibrational frequencies are determined just by the strength of the M– X bonding. So these modes for WX2 are shifted toward higher frequencies with respect to the MoX2 frequencies. However, the opposite results are obtained for E′ and modes involving the vibrations of both metal and chalcogen atoms, as a result of the heavy metal atom in WX2. Additionally, in Fig. 3, the available experimental data[35, 40, 41] are also presented for comparison. Considering the fact that PBE tends to underestimate the phonon frequencies, the experimental data are well reproduced by our calculations.

Fig. 3. Frequencies of the optical modes at Γ -point for monolayer STMD. Experimental data are cited from Refs. [35], [40], and [41]. The insets show the symmetry representations and the corresponding atomic displacements.

3.3. Thermal expansion

To understand further the contributions of the various modes to thermal expansion, the Grü neisen parameters corresponding to different phonon modes for the monolayer MX2 and those in some high-symmetry directions are shown in Fig. 4. A generalized Grü neisen parameter can be given by[42]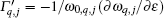, which expresses the Grü neisen parameter as a response of the frequency to thermal strain. From the figure, the Grü neisen parameters for the high-frequency optical branches show very little change in a range between 0 to ∼ 1. For MoS2 and WS2, there are quite strong inter-atomic forces, as revealed by the in-plane stiffness. So their acoustical branches are not strongly affected by the thermal strain, that is, the responses (Grü neisen parameters) do not change much. However, for the other MoX2 or WX2 exhibiting relatively small in-plane stiffness, the Grü neisen parameters for these branches are more scattered as the chalcogen atoms go from Se to Te. Interestingly, for MoTe2 and WTe2, some parameters for LA and TA modes ultimately become negative.

Fig. 4. Calculated mode Grü neisen parameters for monolayers of (a) MoX2 and (b) WX2. In panels (a) and (b), the mode Grü neisen parameters as a function of frequency are presented in the first row, and these values along high-symmetry directions are in the second row. All the mode Grü neisen parameters of the optical phonons are shown without graph legend.

In contrast to graphene, [24] in all the monolayer STMDs only a few Grü neisen parameters for the out-of-plane ZA modes are negative, and most are positive. Based on the Bader analysis shown in Table 1, charge transfer gives rise to an excess charge around chalcogen atoms. Consequently, monolayer MX2 can be viewed as a positively charged metal plane sandwiched between two negatively charged planes of chalcogen atoms. Intuitively, this special sandwich structure forms a strong intra-layer interaction, thus will suppress the so-called membrane effect that can be envisioned as bending induced contraction of the layer. So it is not surprising that the monolayer MX2 crystals only have a few negative Grü neisen parameters for the ZA modes. Also, it is not difficult to speculate that their thermal expansion coefficients will be negative at extremely low temperatures.

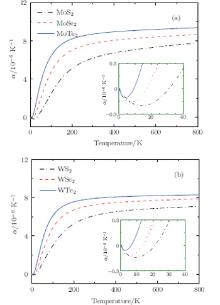
It is indeed shown in Fig. 5 that the linear thermal expansion coefficients for monolayer STMDs exhibit the expected small thermal contractions only in a low-temperature region. The data for MoS2 and MoSe2 obtained by our implementation are in excellent agreement with the reported results.[43] For MoS2, showing the maximum thermal contraction among these compounds, the lattice length decreases gradually as the temperature increases from 0 to 31 K. The minimum value of the linear thermal expansion coefficient is − 2.0× 10− 7K− 1 and occurs at T = 15 K. In this low temperature region the bending modes, which possess very low energy, are responsible for the thermal contraction. At T = 31 K, the lattice length is smallest, and then the thermal contraction turns to an expansion. From 31 K to ∼ 300 K, where more high-energy optical modes are excited, α i(T) increases rapidly with increasing the temperature. Above 300 K this value begins to increase very slowly. For MoTe2 and WTe2, their thermal contractions are relatively small and occur only at T < 9 K and T < 6 K respectively. Moreover, the monolayer STMDs are important in illustrating the general thermal expansion phenomenon in 2D materials.

Fig. 5. Calculated thermal expansions in monolayers of (a) MoX2, and (b) WX2.

When the monolayer MX2 is under an in-plane uniaxial strain arising from thermalization, a useful equation can be expressed as

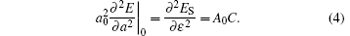
According to Eq. (3), the linear thermal expansion coefficient in terms of the in-plane stiffness C can be written as

Therefore, α i(T) varies inversely with respect to the in-plane stiffness C for monolayer MX2. However, the negative thermal expansion of monolayer MX2 is the result of the bending effect, and is hardly affected by the in-plane stiffness. So equation (5) is not applicable to the negative thermal expansion of monolayer MX2.

Figure 6 shows the variations of charge transfer of metal, in-plane stiffness, and linear thermal expansion coefficients at 300 K for the monolayer STMDs. For MoX2 and WX2, as the chalcogen atoms go from S, Se, to Te, the trends of variation of their thermal expansions are contrary to those of the in-plane stiffness and charge transfers. Moreover, the linear thermal expansion coefficient of WX2 is a little smaller than that of MoX2, because the former possesses a larger in-plane stiffness. Clearly these calculated results well validate Eq. (5) and the relevant discussion mentioned above. In summary, the effects of in-plane stiffness and charge transfers on the thermal expansions of the monolayer STMDs are further clarified. The differences in their positive thermal expansions are determined mainly by the in-plane stiffness. Indeed, these differences can be attributed to the fundamental difference in the level of charge transfer from M to the X atom. In the case of negative thermal expansion, the discrepancies may be due to the difference in bending stiffness among the monolayer STMDs.

Fig. 6. Variations of (a) charge transfers of metal Δ Q, (b) in-plane stiffness C, and (c) linear thermal expansion coefficient α at 300 K for monolayer STMDs.

4. Conclusions

First-principles phonon calculations clearly show the interrelationships among the thermal expansions, in-plane stiffness, and charge transfers in monolayer STMDs. The thermal contraction of monolayer MX2 is very small and appears only at extremely low temperatures. The mode Grü neisen parameters show that the ZA bending acoustic modes are responsible for the contraction, in a direct manifestation of the membrane effect. Their positive thermal expansion coefficients follow the order of MoX2 > WX2 and MS2 < MSe2 < MTe2. These changes can be well explained by the equation

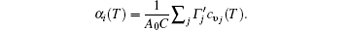
That is, α i(T) varies inversely with the in-plane stiffness C. Essentially, the difference in their positive thermal expansions can be attributed to the fundamental differences in charge transfer from M to the X atom. The observation is beneficial to the practical applications of STMDs and the understanding of the thermal stability of other 2D systems.

Acknowledgment

One of the authors (Z. Y. Wang) is grateful to professor Wang Song-You in Fudan University for their helpful discussion. The calculations were performed on the High Performance Clusters of Zhengzhou University.

Reference
1 Zakharchenko K V, Katsnelson M I and Fasolino A 2009 Phys. Rev. Lett. 102 046808 DOI:10.1103/PhysRevLett.102.046808 [Cited within:1] [JCR: 7.943]
2 Li Z L and Cheng X L 2014 Chin. Phys. B 23 046201 DOI:10.1088/1674-1056/23/4/046201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
3 Reddy C D, Rajendran S and Liew K M 2006 Nanotechnology 17 864 DOI:10.1088/0957-4484/17/3/042 [Cited within:1] [JCR: 3.842]
4 Topsakal M, Cahangirov S and Ciraci S 2010 Appl. Phys. Lett. 96 091912 DOI:10.1063/1.3353968 [Cited within:1] [JCR: 3.794]
5 şahin H, Topsakal M and Ciraci S 2011 Phys. Rev. B 83 115432 DOI:10.1103/PhysRevB.83.115432 [Cited within:1]
6 Coleman J N, Lotya M and O’Neill Aet al. 2011 Science 331 568 DOI:10.1126/science.1194975 [Cited within:1]
7 Chhowalla M, Shin H S, Eda G, Li L J, Loh K P and Zhang H 2013 Nat. Chem. 5 263 DOI:10.1038/nchem.1589 [Cited within:1] [JCR: 21.757]
8 Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N and Strano M S 2012 Nat. Nanotechnol. 7 699 DOI:10.1038/nnano.2012.193 [Cited within:1] [JCR: 31.17]
9 Radisavljevic B, Radenovic A, Brivio J, Giacometti V and Kis A 2011 Nat. Nanotechnol. 6 147 DOI:10.1038/nnano.2010.279 [Cited within:1] [JCR: 31.17]
10 Benameur M M, Radisavljevic B, Héron J S, Sahoo S, Berger H and Kis A 2011 Nanotechnology 22 125706 DOI:10.1088/0957-4484/22/12/125706 [Cited within:1] [JCR: 3.842]
11 Zhao W, Ghorannevis Z, Chu L, Toh M, Kloc C, Tan P H and Eda G 2013 ACS Nano 7 791 DOI:10.1021/nn305275h [Cited within:1] [JCR: 12.062]
12 Tao P, Guo H H, Yang T and Zhang Z D 2014 Chin. Phys. B 23 106801 DOI:10.1088/1674-1056/23/10/106801 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
13 Tongay S, Zhou J, Ataca C, Lo K, Matthews T S, Li J, Grossman J C and Wu J 2012 Nano Lett. 12 5576 DOI:10.1021/nl302584w [Cited within:1] [JCR: 13.025]
14 Miró P, Ghorbani-Asl M and Heine T 2013 Adv. Mater. 25 5473 DOI:10.1002/adma.201301492 [Cited within:1] [JCR: 14.829]
15 Mak K F, Lee C, Hone J, Shan J and Heinz T F 2010 Phys. Rev. Lett. 105 136805 DOI:10.1103/PhysRevLett.105.136805 [Cited within:1] [JCR: 7.943]
16 Lopez-Sanchez O, Lembke D, Kayci M, Radenovic A and Kis A 2013 Nat. Nanotechnol. 8 497 DOI:10.1038/nnano.2013.100 [Cited within:1] [JCR: 31.17]
17 Shi Y, Zhou W, Lu A Y, Fang W, Lee Y H, Hsu A L, Kim S M, Kim K K, Yang H Y, Li L J, Idrobo J C and Kong J 2012 Nano Lett. 12 2784 DOI:10.1021/nl204562j [Cited within:1] [JCR: 13.025]
18 Kwon Y K, Berber S and Tománek D 2004 Phys. Rev. Lett. 92 015901 DOI:10.1103/PhysRevLett.92.015901 [Cited within:1] [JCR: 7.943]
19 Yoon D, Son Y W and Cheong H 2011 Nano Lett. 11 3227 DOI:10.1021/nl201488g [Cited within:1] [JCR: 13.025]
20 Singh V, Sengupta S, Solanki H S, Dhall R, Allain A, Dhara S, Pant P and Deshmukh M M 2010 Nanotechnology 21 165204 DOI:10.1088/0957-4484/21/16/165204 [Cited within:1] [JCR: 3.842]
21 Jiang J W, Wang J S and Li B 2009 Phys. Rev. B 80 205429 DOI:10.1103/PhysRevB.80.205429 [Cited within:1]
22 Belenkii G L, Abdullayeva S G, Solodukhin A V and Suleymanov R A 1982 Solid State Commun. 44 1613 DOI:10.1016/0038-1098(82)90691-3 [Cited within:1] [JCR: 1.534]
23 Abdullaev N A, Suleimanov R A, Aldzhanov M A and Alieva L N 2002 Phys. Solid State 44 1859 DOI:10.1134/1.1514773 [Cited within:1] [JCR: 4.0]
24 Mounet N and Marzari N 2005 Phys. Rev. B 71 205214 DOI:10.1103/PhysRevB.71.205214 [Cited within:3]
25 Murray R and Evans B 1979 J. Appl. Crystallogr. 12 312 DOI:10.1107/S0021889879012528 [Cited within:1] [JCR: 3.343]
26 Kresse G and Furthmiiller J 1996 Comput. Mater. Sci. 6 15 DOI:10.1016/0927-0256(96)00008-0 [Cited within:1] [JCR: 1.878]
27 Kresse G and Furthmüller J 1996 Phys. Rev. B 54 11169 DOI:10.1103/PhysRevB.54.11169 [Cited within:1]
28 Kresse G and Joubert D 1999 Phys. Rev. B 59 1758 DOI:10.1103/PhysRevB.59.1758 [Cited within:1]
29 Blöchl P E 1994 Phys. Rev. B 50 17953 DOI:10.1103/PhysRevB.50.17953 [Cited within:1]
30 Perdew J P, Burke K and Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 DOI:10.1103/PhysRevLett.77.3865 [Cited within:1] [JCR: 7.943]
31 Togo A, Oba F and Tanaka I 2008 Phys. Rev. B 78 134106 DOI:10.1103/PhysRevB.78.134106 [Cited within:1]
32 Ren D H and Cheng X L 2012 Chin. Phys. B 21 127103 DOI:10.1088/1674-1056/21/12/127103 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
33 Wang Z, Wang F, Wang L, Jia Y and Sun Q 2013 J. Appl. Phys. 114 063508 DOI:10.1063/1.4817902 [Cited within:1] [JCR: 0.71]
34 Souvatzis P and Eriksson O 2008 Phys. Rev. B 77 024110 DOI:10.1103/PhysRevB.77.024110 [Cited within:1]
35 Matte H S S R, Gomathi A, Manna A K, Late D J, Datta R, Pati S K and Rao C N R 2010 Angew. Chemie 122 4153 DOI:10.1002/ange.201000009 [Cited within:2]
36 Bollinger M V, Jacobsen K W and Nørskov J K 2003 Phys. Rev. B 67 085410 DOI:10.1103/PhysRevB.67.085410 [Cited within:1]
37 Ataca C, şahin H, Aktürk E and Ciraci S 2011 J. Phys. Chem. C 115 3934 DOI:10.1021/jp1115146 [Cited within:1] [JCR: 4.814]
38 Henkelman G, Arnaldsson A and Jónsson H 2006 Comput. Mater. Sci. 36 354 DOI:10.1016/j.commatsci.2005.04.010 [Cited within:1] [JCR: 1.878]
39 Najmaei S, Ajayan P M and Lou J 2013 Nanoscale 5 9758 DOI:10.1039/c3nr02567e [Cited within:1] [JCR: 6.233]
40 Lee C, Yan H, Brus L E, Heinz T F, Hone J and Ryu S 2010 ACS Nano 4 2695 DOI:10.1021/nn1003937 [Cited within:1] [JCR: 12.062]
41 Rice C, Young R J, Zan R, Bangert U, Wolverson D, Georgiou T, Jalil R and Novoselov K S 2013 Phys. Rev. B 87 081307 DOI:10.1103/PhysRevB.87.081307 [Cited within:1]
42 Schelling P K and Keblinski P 2003 Phys. Rev. B 68 035425 DOI:10.1103/PhysRevB.68.035425 [Cited within:1]
43 Sevik C 2014 Phys. Rev. B 89 035422 DOI:10.1103/PhysRevB.89.035422 [Cited within:1]