Plasma-filled waveguides are an essential component of a variety of microwave sources such as backward wave oscillators (BWO), traveling wave tube (TWT) amplifiers, gyrotrons, and other microwave tubes. The presence of plasma in these devices increases the overall efficiency and, in some cases, reduces the need for guiding magnetic fields. There have been many studies on waveguides partially and completely filled with plasmas. The first detailed analysis of completely as well as partially filled plasma waveguides was carried out by Trivelpiece and Gould.^[1] They measured phase characteristics of space charge waves in finite plasma with a finite axial magnetic field. These longitudinal electrostatic plasma oscillations, modified by the cylindrical boundary, are known as TG waves. Bevc and Everhard^[2] followed their work and they developed a rigorous treatment for the completely filled waveguide for two types of waveguide and cyclotron modes. Fisch^[3] reviewed the theory of current drive in plasmas as well as plasma waves, which included the generation of electron– cyclotron waves and their interaction with electrons at cyclotron resonance. Ghosh and Pal^[4] studied the propagation of electromagnetic waves in a warm plasma-filled cylindrical waveguide and considered the effect of particle collision on the eigenmodes. Further investigation of the electromagnetic treatment of the completely filled as well as partially filled waveguides was performed by Ivanov et al.^[5] Maraghechi et al.^[6] have theoretically analyzed azimuthally symmetric high-frequency eigenmodes of a cylindrical metallic waveguide partially filled with magnetized plasma and discussed the dependence of the dispersion curves on the ratio of plasma radius to waveguide radius. More recently, the effect of electron temperature on the eigenmodes of a plasma-loaded cylindrical waveguide was investigated by Aghamir and Abbasnejad.^[7] Although a number of theoretical studies have been undertaken to analyze the dispersion characteristics of high-frequency guided plasma waves, ^{[8– 11]} almost all of the studies are based on the fluid theory approximation. However, for plasma systems of finite temperature and finite size, the local approximation is not always valid and can miss important physical phenomenon such as Landau damping in the collisionless limit.^{[12– 14]} A kinetic approach is needed to correctly describe the behaviors of these plasmas.

As is well known, there exist two linear mechanisms of collisionless absorption of waves in plasma, namely, Landau damping and cyclotron damping. Knowledge of the absorption processes for the guided plasma waves is important for a deeper understanding of plasma systems. The absorption mechanisms can easily be understood. One can decompose the motion of each charged particle into a force-free streaming along the magnetic field lines and a rotational acceleration leading to perpendicular cyclotron radiation and Cherenkov waves. Landau damping is important for waves whose phase velocity is close to the thermal velocity of charge particles. There are two different mechanisms of Landau damping, linear^[15] and nonlinear processes. The linear Landau damping is associated with those particles in original distribution, which have a velocity nearly equal to the wave phase velocity, namely the “ resonant particles” . The largest contribution comes from the resonance particles in the initial distribution which have not yet traveled a half-wavelength relative to the wave (| v– v_ph| = π /k = λ /2. In continuation of such studies, Malberg and his coworkers ran a series of experiments to demonstrate linear Landau damping.^[16] They measured the spatial damping length of Trivelpiece– Gould (TG) waves in an open-ended neutral plasma column. They used probes to excite and detect plasma waves along a collisionless plasma column and obtained the profile of both phase and amplitude of waves as a function of distance through an interferometer.^[17] The nonlinear Landau damping^[18] occurs when the amplitude of the wave grows and collisionless damping with trapped particles takes place. In this process, the wave does not decay monotonically; rather, the amplitude fluctuates during the decay as the trapped particles bounce back and forth in the potential wells.

Electron– cyclotron resonance (ECR) in plasma is of considerable interest for a variety of industrial applications including the usage of high-density plasma source for plasma processing and material surface modification.^{[19– 22]} Takahashi et al.^[23] and Kaneko et al.^[24] experimentally studied the propagation and damping mechanism of the left-handed polarized wave near the electron– cyclotron resonance. They have demonstrated that the absorption of the left-handed polarized wave near the ECR point in a magnetized inhomogeneous plasma results from polarization reversal in the axial direction. Ganguli et al. have developed a kinetic theory formulation for ECR absorption in a cylindrical microwave discharge.^{[25, 26]}

In the present paper, by simultaneous solution of Vlasov and Maxwell equations, the field components and the dispersion relation of a cylindrical waveguide with a magnetized collisionless plasma are derived. The analysis includes the properties of collisionless damped magnetized plasma. The rest of the present paper is organized as follows. In Section 2, the model and the approach are described, while the derivation of the wave equation is presented in Section 3. The numerical results on wave damping and power deposition are given in Section 4. In Section 5, an analysis of the modes damping behavior is performed. The concluding remarks are presented in Section 6

Consider a plasma column of radius r_p coaxially located in a conducting cylindrical waveguide of radius R with an applied uniform axial magnetic field B₀, which is shown in Fig. 1. The guide axis is taken to be the z axis and the uniform static magnetic field is in the positive direction. The Maxwell curl equations in the waveguide can be written as

where is the dielectric tensor of the magnetized uniform collisionless plasma. A self-consistent kinetic equation is used to obtain the dielectric permittivity in the limit of a collisionless plasma.^[27]

It is assumed that the wavelength of the waves is much smaller than the cylindrical waveguide length. Through the use of Fourier transforms, all of the perturbed quantities in cylindrical coordinates can be written as follows:

The response function of the plasma medium has time and z-component of space nonlocality. The material equation of medium plasma in Fourier space can be expressed as

where

The linear Vlasov equation for the perturbation of the distribution function is given as

where f_0α , δ f_α , Ω _α , and ϕ are the equilibrium (unperturbed) distribution function of α species (α can be electrons and ions), the non-equilibrium (perturbed) distribution function, the cyclotron frequency of α species, and the angle component of the cylindrical coordinate for momentum and space, respectively. Due to the perturbed fields, the induced current density is given as

Finally, using the relationship between the complex dielectric permittivity and the complex conductivity along with the solution of Eq. (3), the dielectric tensor can be written as

where f_0α (ε _α ) is the Maxwellian distribution function, expressed as

Upon substitution of f_0α into the above equation and after performing some algebra, the entire components of the dielectric tensor are obtained as

where

with m_α , T_α , and k_B being the rest mass, the temperature of α species, and the Boltzmann constant, respectively, I₊ (β _α ) the familiar function, ^[13] satisfying the asymptotic expressions

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of the cylindrical plasma waveguide. R and rp are the cylindrical waveguide radius and plasma column radius, respectively.

Using Maxwell equations (Eqs. (1) and (2)), the components of electric and magnetic fields can be derived as follows:

where

Substitution of Eqs. (6)– (9) into the z component of Maxwell’ s equations yields electric and magnetic field components in the direction of the wave propagation as follows:

where

Equations (10a) and (10b) are a pair of inhomogeneous second-order coupled differential equations. The mutual substitution of the electric and magnetic fields in Eqs. (10a) and (10b) leads to the following fourth-order uncoupled wave equations:

A solution with radial dependence in the form of the Bessel function J₀(Kρ ) can be considered for the above wave equations leading to

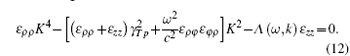
This is one of the basic equations used to compute the dispersion relation. It should be noted that the Bessel function of the second kind diverges on the symmetric axis of the cylinder and is of no interest. Thus the solutions of the z component of the electric and magnetic fields in the plasma region 0 < ρ < r_p can be written as

where

Upon substitution of Eqs. (13) and (14) into Eqs. (6)– (9), the rest of the electromagnetic field components in the plasma region can be derived as follows:

where

Similarly, through the use of Maxwell’ s equations, the field components in the vacuum region can be obtained. After the application of the appropriate boundary conditions to the waveguide wall, namely

The field components can be listed as follows:

The above field components for the plasma and vacuum regions have been used to derive the dispersion relation of the cylindrical waveguide containing the plasma column. The dispersion relation is obtained through the application of the boundary conditions on the vacuum– plasma interface, which are

The imposition of the boundary conditions leads to four linear homogeneous equations, which can be written in the following matrix form:

For nontrivial solutions of the above equations, the determinant of the coefficient matrix, M (the above 4 × 4 matrix) must be zero. The simultaneous solutions of this equation (det M = 0) along with the wave equation (Eq. (12)) provide the dispersion characteristics of the plasma and waveguide modes.

The dispersion relation of a plasma waveguide essentially depends on the geometric boundary of the waveguide, its plasma parametric properties, and the external field configuration loaded on the waveguide. The background free energy in the medium can be the generator of instabilities. As is well known, the amplitude of electromagnetic fluctuation in plasma can be reduced or amplified by instabilities. In the absence of any energy source in the plasma medium, the electromagnetic fluctuations are damped. In this paper, we consider a homogenous and collisionless plasma. Furthermore, it is assumed that the equilibrium distribution function is isotropic. Therefore, the only damping in the system is due to the thermal motion of charge carriers. This weak damping of plasma waves (Landau damping) occurs when the phase velocity of the plasma wave exceeds the thermal velocity of the charge carriers. This indicates that only the fast charges can absorb energy from the plasma wave. By using the dielectric permittivity tensor and the solution of the wave equation along with the application of appropriate boundary conditions, the dispersion properties of a magnetized collisionless cylindrical plasma waveguide can be characterized. The dispersion relation for a real wave-number has a complex frequency solution.^{[2, 3]} In a weakly absorbing transparent medium, the wave damping is weak and the imaginary part of the dispersion relation is much smaller than the real part, i.e., Im {Λ (ω , k)} ≪ Re{Λ (ω , k)}. In this case, the approximate solution of the dispersion equation can be obtained in the form of ω (k) + iδ (k), where ω (k) is the root of the real part of the dispersion equation Re{Λ (ω , k)}= 0 and the damping rate δ (k) of the wave can be written as^[3]

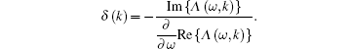
A numerical study is carried out to analyze the solution of the dispersion relation and Landau damping for a cylindrical waveguide containing magnetized collisionless plasma in the symmetric mode (m = 0). There are four families of modes in a partially-filled plasma waveguide, namely, the EH waveguide mode, the HE waveguide mode, the cyclotron mode (C), and the space-charge mode (SC). The EH and HE waveguide modes are the TM and TE modes of an empty waveguide modified by the presence of the magnetized plasma, respectively. These waveguide modes have higher frequencies at a given wave number when the waveguide contains plasma than when it is empty. For the case of a completely filled waveguide, the cyclotron modes have frequencies which are between the upper hybrid frequency, and the cyclotron frequency, ω _ce or plasma frequency, ω _pe, whichever is larger (provided that ω _ce is below the cutoff frequency of the EH₀₁ mode). Each mode is purely transverse electric at k_z= 0, predominantly transverse electric for ω /k_z ≫ c, hybrid for ω /k_z∼ c, and predominantly transverse magnetic for ω /k_z≪ c. In a completely filled guide, the space-charge mode frequencies increase with increasing k_z, and approach to an asymptotic limit as k_z→ ∞ . This limit is ω _pe or ω _ce, whichever is smaller.

We now proceed to study the Landau damping and the dispersion relation along with field profile of a cylindrical waveguide containing magnetized collisionless plasma for the family of four modes versus some plasma parameters such as, electron thermal velocity, plasma column radius, and cyclotron frequency. For the present study, the plasma column and the waveguide radius, the applied external magnetic field, the plasma equilibrium number density, and the thermal velocity of electrons are taken to be R_p = 1.055 cm, R = 1.55 cm, B₀ = 0.19546 T, n₀= 1.0745× 10¹⁷ m^{− 3}, and V_Te/C = 0.03, respectively. All frequencies and wave-numbers are normalized by ω _pe and ω _pe/C respectively. It is assumed that

This indicates that the contribution of ions is negligible. In the limit of β _nα → ∞ , the warm plasma assumption reduces to the condition where the plasma is cold.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Plots of normalized frequency ω /ω pe versus normalized axial wave number kc/ω pe for EH01 waveguide mode. The solid, dashed, and dotted curves represent the cold plasma, the warm plasma with an electron thermal velocity of Vpe/c = 0.02, and the warm plasma with an electron thermal velocity of Vpe/c = 0.002, respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Plots of normalized frequency ω /ω pe versus normalized axial wave number kc/ω pe for SC01 waveguide mode. The solid, dashed, and dotted curves represent the cold plasma, the warm plasma with an electron thermal velocity of Vpe/c = 0.02, and the warm plasma with an electron thermal velocity of Vpe/c = 0.002, respectively.

Figures 2– 4 show the plots of normalized frequency ω /ω _pe versus normalized axial wave number kc/ω _pe for EH₀₁ waveguide mode, as well as, C₀₁ and SC₀₁ plasma modes. The solid, dashed, and dotted curves represent the cold and the warm plasmas with electron thermal velocities of V_pe/c= 0.02 and V_pe/c= 0.002, respectively. The HE₀₁ waveguide mode experiences a similar behavior to the EH₀₁ mode when the electron thermal velocity is taken into account.^[7] As can be noticed from these figures, the electron thermal velocity has almost no effect on each of the normalized frequencies of these three modes. The dispersion characteristics of the cold plasma column (solid curves) are very similar to those presented in Refs. [4] and [5], where the fluid model is not taken into account. Figures 5(a1)– 5(a3) show the plots of normalized Landau damping for EH₀₁, C₀₁, and SC₀₁ modes for three different values of normalized electron thermal velocities.

It should be noted that due to the assumption of a weakly absorbing medium, the three normalized thermal velocities (0.003, 0.002, 0.001) chosen for the plots of the cyclotron mode are an order of magnitude smaller than those (0.03, 0.02, 0.01) considered for the EH₀₁ and SC₀₁ modes. For all three modes, the normalized Landau damping grows as the thermal velocity increases. The inspection of Landau damping plots for these modes also indicates that each of the damping rates increases with the increase of the wave-number. However, at large values of thermal velocities, the damping rates of the EH₀₁ and SC₀₁ modes experience insignificant change.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Plots of normalized frequency ω /ω pe versus normalized axial wave number kc/ω pe for EH01 waveguide mode. The solid, dashed, and dotted curves represent the cold plasma, the warm plasma with an electron thermal velocity of Vpe/c= 0.02, and the warm plasma with an electron thermal velocity of Vpe/c= 0.002, respectively.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Plots of logarithm of normalized Landau damping versus normalized axial wave number kc/ω pe for panel (a1) EH01 mode, panel (a2) C01 mode, and panel (a3) SC01 mode, where the solid, dashed, and dotted curves represent three different values of normalized electron thermal velocity: (a1) (0.03, 0.02, 0.01), (a2) (0.003, 0.002, 0.001), and (a3) (0.03, 0.02, 0.01) respectively; (b) plots of logarithm of normalized Landau damping versus normalized axial wave number kc/ω pe for panel (b1) EH01 mode, panel (b2) C01 mode, and panel (b3) SC01 mode, where the solid, dashed, and dotted curves represent three different values of normalized plasma radius (0.7, 0.65, 0.6), respectively; plots of logarithm of normalized Landau damping versus normalized axial wave number kc/ω pe for (c1) EH01 mode and (c2) SC01 mode, where the solid, dashed, and dotted curves represent three different values of normalized cyclotron frequency (1.86, 1.63, 1.40), respectively.

The plots of the normalized damping rate as a function of the wave-number for EH₀₁, C₀₁, and SC₀₁ modes at three different values of plasma column radius are shown in Figs. 5(b1)– 5(b3), respectively. For each plasma radius, the normalized Landau damping grows with increasing k for all three modes. The damping rate of the waveguide mode (EH₀₁ mode) is much smaller than the plasma modes (C₀₁ and SC₀₁ modes) and experiences a small decrease as the plasma column radius increases. The effects of cyclotron frequency (or applied magnetic field) on the normalized Landau damping of waveguide and plasma modes are presented in Figs. 5(c1) and 5(c2). Three different arbitrary values of normalized cyclotron frequencies are chosen for both EH₀₁ and SC₀₁ modes. For each cyclotron frequency, the Landau damping grows with increasing k for both EH₀₁ and SC₀₁ modes. As shown in Figs. 5(c1) and 5(c2), the damping rates of both modes are larger at higher values of applied magnetic field.

The electric field profile along the symmetric axis of the plasma waveguide (the direction of the wave propagation) shows considerable dumping over a meter long range. Figures 6(a)– 6(c) represent the effects of Landau damping on the field profile for different plasma parameters. The effects of the thermal velocity on the field profile and the damping rate are shown in Fig. 6(a). The solid curve in this figure represents the field profile for the normalized thermal velocity of 0.001 while the dashed one indicates the case for the normalized thermal velocity of 0.003. As the thermal velocity increases or in other words the Landau damping grows, the amplitude of the propagating electric field decreases. The increase in either the plasma column radius or the applied magnetic field (or normalized cyclotron frequency) has an insignificant effect on the damping process and the reduction of the field amplitude, as depicted in Figs. 6(b) and 6(c), respectively. In Fig. 6(b), two arbitrary values of 0.6 and 0.7 are chosen for the normalized radius. The two normalized cyclotron frequencies used for the field profile simulation in Fig. 6(c) are 1.4 and 1.86, respectively. In order to investigate the nature of field polarization and to find how well the generated waves can be coupled out of the plasma system, the effect of Landau damping on the radial field profile is looked into. Figures 7(a) and 7(b) show the plots of the magnitudes of the normalized electric field radial component and the field polarization versus the logarithm of Landau damping, respectively. The solid curves in both figures represent the case of a plasma column with a normalized radius of 0.22, while the dashed curves belong to a column with a normalized radius of 0.29. A closer examination of the plot of field polarization versus plasma column normalized radius (Fig. 7(c)) indicates that for normalized radii smaller than 0.24, field polarization turns larger and at the same time Landau damping becomes considerable. The opposite scenario occurs for radii larger than 0.24.

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. Plots of normalized electric field versus axial distance, where the solid and dashed curves represent the electric fields of (a) the warm plasma with two different values of normalized thermal velocity (0.001 and 0.003), (b) the plasma column with two different values of normalized radius (0.6 and 0.7), respectively, and (c) the plasma column with two different values of normalized cyclotron frequency (1.4 and 1.86), respectively.

Fig. 7.

Figure Option ViewDownloadNew Window

Fig. 7. (a) Plots of logarithm of field polarization versus logarithm of normalized Landau damping and (b) plots of normalized radial field magnitude versus logarithm of normalized Landau damping, where the solid and dashed curves represent the plasma column with two different values of normalized radius (0.22 and 0.29), respectively; (c) plot of logarithm of field polarization versus plasma column normalized radius.

The effects of thermal velocity and Landau damping on the frequency spectrum of a propagating wave in a cylindrical plasma waveguide are investigated. The analysis is based on kinetic theory and solutions of the wave equation. A numerical analysis is carried out to study the solutions of the dispersion relations and the effects of Landau damping for a family of four waveguide and plasma modes. The analysis indicates that the electron thermal velocity has insignificant effects on the normalized frequencies of these modes. However, the Landau damping grows as the thermal velocity increases. It is found that the plasma waves (space-charge and cyclotron modes) experience a small increase in damping rate with the increase of plasma column radius, while the waveguide modes remain unaffected. Finally, the Landau damping grows as the applied magnetic guide field increases.