The GW approximation is based on the set of Hedin's equations that, when solved self-consistently, yield the exact interacting single-particle Green function.^[9] In the GW approximation, the vertex corrections are neglected, resulting in a simplified self-energy Σ _xc equation, i.e.,

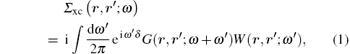
where δ is a positive infinitesimal number, and G and W are the electron Green function and dynamically screened Coulomb interaction, respectively. Hedin’ s equations even in the GW approximation form are still very complicated. In practice, further approximations are introduced, in which both G and W operators are constructed in the quasi-particle approximation by using the Kohn– Sham wave functions ψ _n and energies e_n obtained from the DFT calculations. Therefore, it is called the G₀W₀ or one-shot GW approximation, where G₀ is the electron Green function and is given as

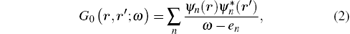
and W₀ is the dynamically screened Coulomb interaction

with V being the bare Coulomb interaction, and ε ^{− 1} the inverse dielectric matrix.

The energies ε _n are calculated by using the first order perturbation theory, and the perturbation is written as

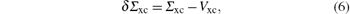
where V_xc is the exchange correlation potential perturbation. The energies

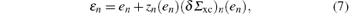
where

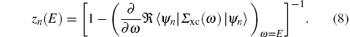
When a light beam transmits through a crystal, the crystal will be polarized by the electric field E. For a weak electric field, the relation between the dielectric polarization P and E is linear. For a strong electric field, however, the linear relation is no longer valid and we can write P as a power series of the electric field as follows:

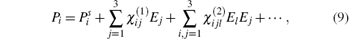
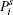
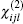
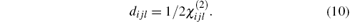
where is the zero-field polarization. In the literature dealing with nonlinear optics, one often finds another definition of the NLO susceptibility. Instead of , it is more convenient to rely on the d tensor defined as

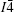
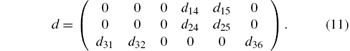
The matrix of d_ijl consists of 18 tensor elements. According to the symmetry of space group, the nonzero elements are listed as follows:^[10]

According to Kleinman symmetry, ^[10] which was devised by Kleinman in 1960, d₂₄ = d₃₁ = d₃₂ = d₁₅ and d₃₆ = d₂₅ = d₁₄. So, only d₁₄ and d₁₅ have nonzero values in the matrix element of d_IJ, I = 1, 2, 3; J = 1, 2, 3, 4, 5, 6.

According to the DFPT, ^[11] we can relate the NLO susceptibilities to a third-order derivative of the energy with respect to an electric field as follows:

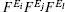
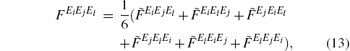
where Ω ₀ is the unit volume and is defined as

and

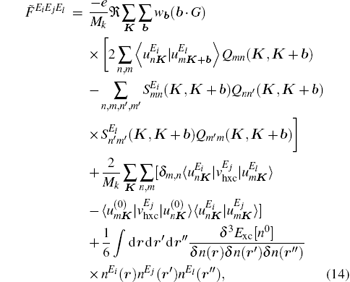
where M_k is the number of k-points, M_k = 4× 4× 4 = 64, E_xc is the exchange– correlation energy function, n(r) is the ground-state density, ν _hxc is the exchange– correlation potential which is a function of the ground-state density n(r), b is the vector connecting a k-point to one of its nearest neighbours, w_b is a weight factor, G is a basis vector of the reciprocal lattice, S is the overlap matrix between Bloch functions at K and K + b, Q is the inverse of the overlap matrix S, and u is the projection of the first-order wave function on the conduction band.

The total energy, electronic structure, band gap, and second-order NLO susceptibilities are calculated using the ABINIT software package.^[12] During the calculation, norm-conserving pseudopotential^[13] was used, the cut-off energy is 22 Hatree (1 Hatree = 27.2114 eV), and the k-point grid is 4× 4× 8 Monkhorst– Pack^[14] in the irreducible Brillouin zone. At first, the structure of CMTC crystal is optimized. The structure is relaxed until the tolerance for absolute difference of total energy below 1.0× 10^{− 9} Hartree (1 Hartree = 27.2114 eV) is reached. The band number is set to be 400 to guarantee the converge.

The space structure of the CMTC crystal is shown in Fig. 1. The CMTC crystal belongs to a tetragonal crystallographic system, 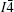a space group. The lattice constants and bond lengths of CMTC crystal are listed in Table 1. One can see from Table 1 that the calculated lattice constants and bond lengths are in agreement with the experimental data.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Space structure of CMTC crystal.

Table 1.

Table 1.

Table 1. Lattice constants and bond lengths of CMTC crystals. Lattice constant/nm Calculated value Experimental value[1] a 1.148 1.149(2) c 0.433 0.425(2) Bond lengths/nm Calculated value Experimental value[15] S– C 0.164 0.1655(8) C– N 0.111 0.1148(11) Cd– N 0.220 0.2174(8) S– Hg 0.259 0.2574(2)

Table 1. Lattice constants and bond lengths of CMTC crystals.

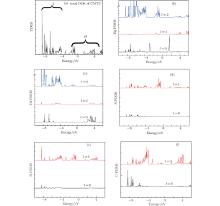
In order to obtain an insight into the contributions to the band structure from Cd, Hg, S, C, and N, the total density of states (TDOS) and partial density of states (PDOS) are computed using a smearing technique and obtained from the eigenvalues, properly weighted at each k point. The calculated TDOS spectrum of the CMTC crystal is shown in Fig. 2(a). The PDOS is computed by using the tetrahedron method. We show the PDOS spectra as well as the angular-momentum projected (l = 0, 1, 2) DOS in Figs. 2(b)– 2(f) in which the orbitals l = 0, 1, 2 represent s, p, and d orbitals, respectively.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) TDOS, (b) Hg-PDOS, (c) Cd-PDOS, (d) S-PDOS, (e) N-PDOS, (f) C-PDOS of CMTC crystals.

The TDOS spectral lines are divided into H and I groups, as shown in Fig. 2(a). By comparing them with PDOS spectral lines of CMTC crystal (Figs. 2(b)– 2(f)), it can be concluded that the peak I (from − 8.57 eV to − 0.41 eV) is for the valence band which is formed mainly from Cd-4d, Hg-5d states, and the valence band top predominantly comes from C-2p, N-2p, and S-3p states. The H group (2.04 eV to 6 eV) is for the conduction band, which is dominantly formed by the C-2p and N-2p states.

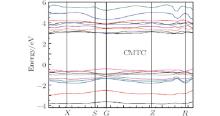
The structure of electronic bands for the CMTC crystal in the vicinity of the forbidden gap is shown in Fig. 3. As can be seen from the figure, the energy band trend is gentler and the bandwidth is small, which is consistent with the complex compound structure of the CMTC crystal. It can be seen that the bottom of conduction band and the top of valence band are both at the same point G in the Brillouin zone. Thus, the CMTC crystal is a direct band gap crystal. The calculated energy gap of CMTC is 3.198 eV, which is close to the experimental value of 3.265 eV.^[16]

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Energy band of CMTC crystal.

Second-order NLO susceptibilities (i.e., SHGs) are studied by using DFPT, and the parameters used are kept the same as the calculations in the GW approximation. Table 2 presents the SHG of CMTC crystal. One can notice from Table 2 that the SHGs of the CMTC crystal are in agreement with the experimental values.

Table 2.

Table 2.

Table 2. Second-order nonlinear optical susceptibilities of a CMTC crystal. Second-order NLO coefficient Calculated value Experimental [17] value d14/(pm/V) 1.2906 1.4 ± 0.6 d15/(pm/V) 5.0928 6.0 ± 0.9

Table 2. Second-order nonlinear optical susceptibilities of a CMTC crystal.

The second-order NLO effect of crystal is mainly due to the electronic transition between the valence band top and the conduction band bottom, ^[18] which indicates that the electron transition in CMTC crystal is the dominant mechanism for SHG. In order to investigate the NLO effect in detail, in this paper the SHG dependence on energy band of CMTC crystal is studied using the energy band structure decomposition method. It is found that occupied states above − 1 eV have a significant effect on the SHG of a CMTC crystal, while the unoccupied states between 3 eV and 6 eV are the main sources for NLO properties. Compared with PDOSs shown in Fig. 2, these occupied states come mainly from N-2p and S-3p orbitals, and the unoccupied states originate mainly from C-2p and N-2p orbitals. Therefore, we can conclude that the SHG effect of CMTC results from the electron transition between the valence band (containing N-2p and S-3p orbitals) and the empty band (containing C-2p and N-2p orbitals).