Demand is growing for new laser sources radiating within the specific frequency ranges necessary for optical tracing of molecules and atoms in the near- and mid-infrared region, ^[1] and for terahertz spectroscopy in the far-infrared region, using optically-pumped semiconductor devices.^[2] A number of coherent sources, such as quantum cascade, ^[3] distributed-feedback quantum cascade, ^[4] and all solid-state lasers based on newly developed active materials like Nd:YVO₄, ^[5] Er:YAG, ^[6] and Yb:YAG, ^[7] have been used extensively and developed for a relatively broad region of the spectrum. A recent example is a 2.05-μ m Q-switched laser based on the newly developed material Tm, Ho:GdVO₄ for pumping an optical parametric oscillator to obtain 419-mW radiation at 8.04  μ m with tuning characteristics of ∼ 700  nm.^[8] In addition, in recent years, many applications of short-wavelength radiation in ultraviolet have been found in materials processing^[9] and medical treatment.^[10] Due to the sensitivity of many chemical compounds to ultraviolet radiation, numerous efforts have been directed toward on-line, in-situ monitoring of chemical reactions. One example is the fluorescence imaging of petroleum accelerants, using the third and fourth harmonic wavelengths of a pulsed Nd:YAG laser.^[11] A similar approach is applied for the corrosion control of industrial plants and many hazardous metallic structures.^[12] With the generation of large third-harmonic susceptibility in polymer composites, all-optical signal processing using very fast-response electronic devices have also been realized and introduced as cost-effective means for optical communication and information processing; for example, in all-optical switching and optical data storage.^[13]

The capability of generating very short pulses at high output powers using nonlinear optical phenomena has made solid-state lasers a very practical alternative to gas lasers as reliable ultraviolet sources.^[14] To date, mainly nonlinear materials have been proposed and used in optical frequency conversion for solid-state and gas lasers to obtain ultraviolet radiation sources. Among these, a silicon nitride film with the third-order susceptibility of ∼ (2.8 ± 0.6) × 10^{− 20}  pm/V is used to obtain the third-harmonic radiation from an Nd:YAG laser in the ultraviolet region.^[15] The very low conversion rate is compensated by fabricating a resonant waveguide grating onto the film. However, it is found that the efficiency of the single-pass third-harmonic generation can be enhanced by using a cascade configuration, which has been widely demonstrated as an impressive scheme to achieve higher conversion, along with better stability and beam quality.^{[16, 17]} It is followed by two parametric processes, where in the first step the second-harmonic beam of a laser pump is generated in one nonlinear crystal. Then, the chain of this conversion will be completed by producing ultraviolet radiation through sum-frequency mixing of the residual pump and the second-harmonic beams in a phase-matched crystal. In this context, a 5.7-W deep blue laser at 447  nm is generated by using an LiB₃O₅ crystal for the second-harmonic generation and KTiOPO₄ for sum-frequency interaction.^[18] In a similar demonstration, a CsB₃O₅ crystal is substituted as the sum-frequency generation medium to achieve conversion efficiency of 13.3%, gaining 17.7  W of pulsed third-harmonic power at 355  nm for 140  W of fundamental pump power provided by a high power diode pumped Nd:YAG laser.^[19] Higher conversion efficiency of 40% is also obtained by generating the third-harmonic radiation at 355  nm from a nanosecond Yb-fiber laser using an LiB₃O₅ crystal, a configuration which is selectively shown as a promising candidate for frequency mixing.^[20] The combination of an LiB₃O₅ and a newly developed K₂Al₂B₂O₇ nonlinear crystal in a dual second-harmonic generation scheme has also been reported for generating an efficient 266-nm ultraviolet beam at a conversion efficiency of 13%.^[21] In this framework, two GaSe crystals are used for the third harmonic generation from a high power nanosecond CO₂ laser to obtain 23  W at 3.53  μ m at 0.13% conversion efficiency.^[22]

The most popular crystals for the third-harmonic generation in a cascade scheme are KTiOPO₄ and β -BaB₂O₄ because they have a high damage threshold, moderate nonlinearity, and ease of growth.^{[23, 24, 25]} Hence, the second-harmonic generation of an Nd:YAG laser beam can be initially attained using type-II phase-matched KTiOPO₄, and the third-harmonic beam finally emerges from a type-I β -BaB₂O₄ crystal.

This scheme, however, suffers from an extraordinary third-harmonic beam walk-off, which degrades the maximum attainable efficiency of conversion. The main consequence of the walk-off is the reduction of the effective interaction length and the degradation of the beam profile. This is due to the tight focusing of input Gaussian beams inside the crystal and subsequent reduction of the acceptance bandwidth in the interaction. To compensate for the walk-off, several approaches have been implemented with the aim of maximizing the conversion efficiency. One solution is based on the use of a twin-KTiOPO₄ crystal device in the cavity-enhanced arrangement for single-pass second-harmonic generation.^[26] It consists of two identical crystals with crossed optical axes. A similar device using two β -BaB₂O₄ crystals has also been investigated at 266  nm to increase the angular acceptance of the second crystal, and its effect on the performance of such a walk-off compensation device has been investigated.^{[27, 28]} Referring to prior work, this results in larger acceptance angles, providing higher efficiency and upgrading the beam profile of the generated third-harmonic beam. Another approach is based on a theoretical investigation of a periodic multicrystal configuration and its properties for walk-off compensation in an ultrashort pulsed second-harmonic generation scheme.^[29] In the deep-ultraviolet region, the second-harmonic generation walk-off is also compensated by two β -BaB₂O₄ crystals in a crossed scheme in order to provide the required high quality beam for the generation of 3.72-W power at 193  nm inside a prism-coupled KBe₂BO₃F₂ nonlinear crystal.^[30]

In this paper, we describe a very simple model to investigate the possibility of walk-off reduction by rotating an external optical plate around the beam direction. We found that BK7 glass is theoretically capable of reducing the walk-off by about 13% to 45% when it is rotated to about 35° from normal to the beam direction. The same trend is also obtained by varying the thickness of the BK7 glass plate when it is turned and fixed at 35° for calculation. The validity of the above model is verified by the experimental setup, in which a cascade configuration is used to generate ultraviolet light from a Gaussian-profile Q-switched Nd:YAG laser beam using two consecutive KTiOPO₄ and β -BaB₂O₄ crystals cut for type  II and type  I, respectively. It is performed by rotating a variable-thickness BK7 external plate around the ultraviolet beam direction within the accuracy of ± 30  seconds. This results in a walk-off reduction of about 13% from ∼ 69.33  mrad to ∼ 60.50  mrad. The same results are obtained by varying the thickness of the BK7 plate at a fixed angle. In all cases, very good agreement between the theoretical results and experimental measurements was obtained.

During the experiment, we further observed that, because of the walk-off effect, the beam profile of the emerged ultraviolet light was slightly degraded. Therefore, we used an axicon lens to produce a Bessel– Gauss profile for the fundamental and second-harmonic beams in order to investigate the walk-off effect and its influence on the profile of the resultant third-harmonic beam. Due to the quasi-nondifractive nature of a Bessel– Gauss beam, ^[31] and hence providing larger acceptance bandwidth, a walk-off angle of ∼ 48.81  mrad was measured. Compared to the measured walk-off angle of ∼ 69.33  mrad for Gaussian interaction, a reduction of ∼ 30% is obtained. By using the rotating BK7 glass plate, it is further reduced to ∼ 38.9  mrad while the plate is gradually turned 35° , corresponding to ∼ 45% reduction in the walk-off angle. The same trend is obtained by changing the thickness of the BK7 plate at a fixed tilt angle. Besides the walk-off reduction, we observed that the intensity profile of the outcoupled Bessel– Gaussian third-harmonic beam is not substantially affected by the walk-off, providing a third-harmonic beam profile without significant degradation, as expected.

This model is based on a simple theory in geometrical optics. As light travels through a parallel dielectric slab of a certain thickness, it is diverted slightly from its initial direction. The situation is shown schematically in Fig.  1.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic diagram of a light beam displaced by d as it travels through a dielectric slab.

Referring to the figure, we can easily obtain that

where θ is the angle of incidence, t is the slab thickness, and n₁ (λ ) is the material dispersion of the plate, which can be obtained using the relevant Sellmeier equations. As can be seen, besides other variables, the amount of beam walk-off, d(λ ), is very sensitive to the wavelength of incident light. This is very advantageous if such optical configuration is arranged for a sum-frequency-based third-harmonic generation because the wavelength of interacting waves is within a relatively wide range from ultraviolet (UV) to infra-red (IR). Accordingly, Figure  2 shows the same configuration being used to compensate for the third-harmonic generation walk-off.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The same arrangement as shown in Fig.  1 is used to compensate the walk-off angle of extraordinary third-harmonic generation beam.

From the simple geometry in the above figure, it can be clearly shown that

Therefore, in order to completely compensate for the walk-off, we need to have Δ d = 0 and hence

By substituting Eq.  (1) into Eq.  (3) for beam displacements d_i and using a desirable slab material with adequate dispersion, reduction of walk-off is then possible by simply rotating the plate. Among the available optical materials possessing sufficient transparency at the interacting wavelengths, we arrived with BK7, SiO₂, CaF₂, and MgF₂ as the most applicable and transparent materials from UV to IR. Figure  3 illustrates the simulation results for the walk-off calculation as the optical plate is turned through a wide range of rotated angles. The most recent Sellmeier equations for the above materials have been used in this calculation.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Variation of ❘ dSHG − dTHG❘ for a wide range of angles with respect to the beam direction. The thickness of the proposed optical plates is assumed to be t = 20  mm.

As can be seen from the plot, the maximum of ❘ d_SHG– d_THG❘ is obtained by using a rotatable BK7 plate. This shows great advantage for reduction of the third-harmonic generation. It can be further observed that the lowest walk-off angle is obtained with the BK7 plate rotated to ∼ 35° .

The experimental setup that is used to generate the third-harmonic radiation is shown in Fig.  4.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Optical arrangement for the generation of ultraviolet third-harmonic light. A microchip Nd:YAG crystal embraced by a Cr+ 4:YAG slab as Q-switch element is used for a fundamental pump (red arrow). A type II KTiOPO4 crystal is used to generate the second-harmonic radiation (green arrow) while the third-harmonic beam (blue arrow) is generated by a type-I β -BaB2O4 crystal.

As is clear in the figure, a Q-switched Nd:YAG laser is used as the fundamental pump source for the cascading nonlinear interaction in a sequential scheme including KTiOPO₄ and β -BaB₂O₄ crystals. The output of a 2-W diode laser is focused inside a 4-mm-long laser cavity consisting of an Nd:YAG crystal embraced by a Q-switch Cr^{+ 4}:YAG slab element to generate an average output power of ∼ 160  mW. By using the knife-edge technique, the spot size of the outcoupled laser beam is measured as ∼ 1  mm. The pulse length of this Nd:YAG laser beam is measured to be 12  ps using an interferometric autocorrelator. By using a high speed Si PIN detector (Thorlabs, DET110), its pulse repetition rate is measured to be ∼ 4  kHz. This results in ∼ 3.5-MW peak power for the Q-switched Nd:YAG laser. To avoid modulation of the output power, the temperature of the Nd:YAG crystal was controlled using a Peltier element with an accuracy of ± 0.1  ° C. For optimum conversion efficiency inside the nonlinear crystals, the elliptical polarization of the outcoupled beam is characterized and adjusted using a polarized beam splitter cube. This leads to ∼ 110   mW and ∼ 53  mW for e-wave and o-wave, respectively.

As determined by Boyd– Kleinman criteria, the best performance of a nonlinear conversion can be obtained by fixing the confocal parameter at 2.84 and focusing the input beams at the center of the crystal. This in turn is determined by the beam quality of the focusing beam, which indicates the intensity distribution in the beam's cross section. Thus, a 50-cm-focal lens is used to characterize the quality of the Nd:YAG output beam before it enters the KTiOPO₄ crystal. This is performed by using the knife-edge technique along with the ISO standard method. The results of our measurement are shown in Fig.  5.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Nd:YAG beam characterization, performed by moving a knife-edge normal to the beam direction through the x and y axes and using the ISO standard method. The solid lines are the mathematical fit to experimental data.

From the plot, the beam quality of Nd:YAG laser in the two directions was determined to be and , indicating a nearly Gaussian profile. The Q-switched Nd:YAG laser beam with such character was then imaged into a 1-cm-long anti-reflection coated KTiOPO₄ crystal cut for φ = 23.1° and θ = 90° , required for the generation of the second-harmonic radiation in a type-II phase-matching scheme. We achieved a conversion efficiency of ∼ 56%, corresponding to ∼ 14-mW second-harmonic generation power at 532  nm. By using the same method used for the fundamental beam, the pulse width of the generated second-harmonic beam was measured to be 7 ps, providing a peak pulse power of ∼ 0.6  MW.

The residual fundamental and the second-harmonic beams were directed toward a 10-cm-long anti-reflection coated β -BaB₂O₄ crystal to generate the third-harmonic of the Nd:YAG laser at 355  nm. The β -BaB₂O₄ crystal was cut for θ = 31.1° and φ = 90° , as is necessary for type-I phase-matching in which the polarization of the input beams is adjusted as o-waves. By very tight focusing of the fundamental and the second-harmonic beams, e-wave ultraviolet third-harmonic generation was then radiated at a measured conversion efficiency of 13%. Following the formula given in the standard textbooks, we calculated the walk-off angle of the third-harmonic e-wave as ρ ≃ 72   rad. In order to experimentally measure the walk-off angle, a knife edge is scanned in the xy plane over the cross sections of the second- and third-harmonic beams to obtain the separations of the two intensity peaks, Δ x(= ❘ x_SHG − x_THG ❘ ) and Δ y(= ❘ y_SHG − y_THG ❘ ), required for 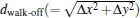calculation. Therefore, we obtained Δ x = 0.58  mm and Δ y = 0.38  mm, corresponding to d_walk-off = 0.693  mm. By using the simple relation ρ = tg^{− 1}(d_walk-off/L_BBO), the walk-off angle of ρ ≃ 69.33  mrad is obtained, confirming very good consistency between the calculation and the measurement. The physical consequence of the walk-off effect is the group velocity mismatch in harmonic generation, which leads to damage of the intensity profile, as has been reported. Figure  6 shows the traced beam profile of the pulsed third-harmonic generation, which is captured by a CCD camera behind a semi-transparent screen.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Intensity profile of traced ultraviolet third-harmonic light, using a CCD camera and Max Im DL interface.

As is evident in the figure, the intensity profile of the peak is slightly degraded and deviates from Gaussian form. This can be repaired if the walk-off is compensated or reduced, even by a small amount.

Figure  7 shows the optical arrangement used to verify the simulation results in Fig.  3 and the related discussion.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Optical arrangement used to reduce the walk-off angle, employing a BK7 plate of variable thickness that can be rotated with respect to the third-harmonic (blue arrow) beam. An optical filter is used to block the fundamental beam.

A 20-mm-thick BK7 plate consisting of ten 2-mm-slabs is used to reduce the walk-off angle of the third-harmonic light. It is then gradually rotated with respect to the direction of the third-harmonic beam with an accuracy of ± 30  sec. Similarly, in measuring the walk-off angle, the cross section of the passed beams is scanned by a knife-edge over the xy plane in order to measure the second- and third-harmonic intensity peak separations, Δ x and Δ y, hence obtaining d_walk-off . The results of our measurements are shown in Fig.  8.

Fig.  8.

	Figure Option '>ViewDownloadNew Window
'>	Fig.  8. Reduction of the third-harmonic generation walk-off angle while the 20-mm-thick BK7 plate is rotated up to 35° around the beam's direction. The BK7 thickness is kept constant during the measurement. The calculated walk-off angle is given for comparison.

As can be seen, by increasing the rotating angle of the BK7 plate up to 35° , the third-harmonic generation walk-off angle is reduced to ∼ 60.5  mrad, which is a ∼ 13% relative reduction. The same trend can be observed in the theoretical calculation, confirming the validity of our numerical model, which is provided by a simple theory. To study the effect of BK7 thickness on the walk-off, it was fixed at a 35° angle, where the minimum walk-off was obtained, and then its thickness was regularly changed from 20  mm to 2  mm. The walk-off angle was measured again using the knife-edge technique and the same concepts as used in plotting Fig.  8. The results of these measurements are plotted in Fig.  9.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Variation of the third-harmonic generation walk-off angle with the thickness of the BK7 plate while it was fixed at the angle of 35° . Theoretical results are included to corroborate the measurement.

As can be observed from the results depicted in the plot, the important feature of using thicker BK7 plates is the decrease in the third-harmonic generation walk-off angle from 69.33  mrad to 60.61  mrad. The same behavior can be seen in the calculation, confirming again the performance of our theoretical approach. However, as is evident from these results, the third-harmonic generation walk-off is more sensitive to the BK7 thickness than to the rotating angle, by a factor of ∼ 3.5.

In order to further reduce the walk-off and compensate for the observed degradation in the beam profile of the generated third-harmonic light, an axicon lens (EKSMA optics) with an apex angle of 178° is used to redistribute the intensity of the interacting beams from a Gaussian pattern to a Bessel– Gaussian form. This, as expected, leads to an increase of the β -BaB₂O₄ acceptance angle and, hence, reduces the walk-off effect. The non-diffractive nature of an ideal Bessel– Gaussian beam has made it useful for many applications in general and for optical frequency conversion in particular. The mathematical description of a Bessel– Gaussian beam is fully discussed in many scientific documents.

To enhance the efficiency of conversion and increase the interaction area, the zero-order Bessel– Gaussian beam was generated using an optical configuration including a combination of a convex lens and axicon. This arrangement mean that we were able to change the Bessel– Gaussian spot size of the fundamental and the second-harmonic beams through simply varying the separation of the convex lens and the axicon. This changed the Nd:YAG beam spot size before it hit the axicon surface, and consequently changed the spot size of the zero-order Bessel– Gaussian second-harmonic beam, as shown in Fig.  10.

Fig.  10.

	Figure Option ViewDownloadNew Window
	Fig.  10. Reduction of the Bessel– Gaussian second-harmonic generation spot size behind the axicon by increasing the spot size of the Nd:YAG beam before hitting the axicon surface. This was performed by changing the distance separating the convex lens and the axicon.

As can be seen from the plot, by expanding the Nd:YAG beam size to ∼ 7.75  mm on the axicon surface, a zero-order Bessel– Gaussian second-harmonic generation spot size of ∼ 42  μ m is obtained. An example of a digitized beam profile of such a generated Bessel– Gaussian second-harmonic beam is shown in Fig.  11.

Fig.  11.

	Figure Option ViewDownloadNew Window
	Fig.  11. The beam profile of the generated zero-order Bessel– Gaussian second-harmonic beam traced using a CCD camera and Max Im DL digitizer.

As is clearly evident from the plot, the trace of the generated second-harmonic beam has a zero-order Bessel– Gaussian form.

After optimizing the Bessel– Gaussian beams, we started with w₀ = 160  μ m and w₀ = 85  μ m for the spot sizes of the fundamental and second-harmonic beams, respectively, to generate Bessel– Gaussian third-harmonic radiation through very tight focusing of the input beams inside the β -BaB₂O₄ crystal. Following the same procedure, the walk-off angle of the generated ultraviolet third-harmonic light is then measured to be ρ = 48.81  mrad by using the knife-edge technique. This resulted in a ∼ 30% reduction compared with that measured in the Gaussian interaction as described above. To further reduce the walk-off, we used the same BK7 plate along with a knife edge to measure the separation of the second- and third-harmonic generation peak intensities in the xy plane, as required for obtaining the walk-off angle. This was accomplished by rotating the 20-mm-thick BK7 plate over a range of angles and scanning the second- and third-harmonic beam cross sections. The results of these measurement are illustrated in Fig.  12.

Fig.  12.

	Figure Option ViewDownloadNew Window
	Fig.  12. Measured Bessel– Gaussian third-harmonic generation walk-off angle performed by rotating the BK7 plate up to 35° around the Bessel– Gaussian beam. The BK7 thickness is kept at 20  mm during the measurement.

It can be seen that while the BK7 plate is rotated up to 35° , the walk-off angle tends to ∼ 38.9   mrad, corresponding to a ∼ 20% reduction. As illustrated in Fig.  13, similar results are obtained by varying the thickness of the BK7 slab while it is tilted at 35° .

Fig.  13.

	Figure Option ViewDownloadNew Window
	Fig.  13. Reduction of Bessel– Gaussian third-harmonic generation walk-off angle versus the thickness of BK7 plate while it is tilted at 35° during the measurement.

A similar trend in the walk-off reduction can be seen when the thinner BK7 plates are rotated to larger walk-off angles. To observe the effect of the Bessel– Gaussian on the beam-profile of the third-harmonic generation, the same CCD camera was used to provide a two-dimensional slice using the MaxImDL interface. Figure  14 shows the traced intensity profile of the Bessel– Gaussian third-harmonic generation beam, captured behind an ultraviolet-sensitive screen.

Fig.  14.

	Figure Option ViewDownloadNew Window
	Fig.  14. Two-dimensional intensity profile of the generated Bessel– Gaussian third-harmonic beam, captured by a CCD camera and MaxImDL software. The profile of Gaussian third-harmonic beam shown in Fig.  6 is included for comparison.

As is evident, the effect of Bessel– Gaussian interaction on the intensity profile is apparent where the Bessel– Gaussian feature of the generated third-harmonic beam is completely preserved with no significant impact of walk-off.

By using the output beam of a Gaussian-profile Q-switched Nd:YAG laser as the fundamental pump source, an extraordinary phase-matched third-harmonic beam is generated in a cascade configuration. This is achieved by generation of its second harmonic green light at 532  nm in a type-II KTiOPO₄ crystal and sum-frequency mixing with its fundamental beam in a type-I β -BaB₂O₄ crystal. A theoretical walk-off angle of 72  mrad is calculated, while in experiment it is measured to be 69.33  mrad. A simple theoretical model is developed in order to find a way to reduce the walk-off angle of the generated third-harmonic beam. It is based on the rotation of a BK7 plate of variable thickness off the beam direction. We obtained ∼ 13% reduction in the third-harmonic generation walk-off as the 20-mm-thick BK7 plate was gradually rotated up to 35° . By varying the plate thickness, the walk-off angle was also reduced to 60.50  mrad by a similar trend. The same phenomenon was confirmed by calculations based on our theoretical model. It was further observed that the intensity cross section of the radiated Gaussian third-harmonic beam is degraded due to the effect of walk-off on the acceptance bandwidth of interacting input beams inside the β -BaB₂O₄ crystal. In order to compensate for such observed degradation and to obtain further reduction of the walk-off, we used an axicon lens to make a zero-order Bessel– Gaussian third-harmonic beam in the same cascade configuration. By this transformation, the walk-off angle is decreased to 48.81  mrad, providing ∼ 30% reduction when compared to the case of Gaussian interaction. The same rotatable BK7 plate is also used to reduce the walk-off to 38.9 mrad, a ∼ 20% relative reduction and a total reduction of ∼ 45%. The key feature of using the axicon lens in the above interaction is that the beam profile of the extraordinary generated third-harmonic beam remained unchanged, with no observed degradation. In summary, by the production of a Bessel– Gaussian profile for the interacting fundamental and second-harmonic beams, combined with a simple optical plate, the walk-off angle of the third-harmonic generation wave is minimized, while its intensity cross section was neither affected nor degraded.