Corresponding author. E-mail: yjxia@mail.qfnu.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 61178012, 11204156, 11304179, and 11247240), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant Nos. 20133705110001 and 20123705120002), the Scientific Research Foundation for Outstanding Young Scientists of Shandong Province of China (Grant No. BS2013DX034), and the Natural Science Foundation of Shandong Province of China (Grant No. ZR2012FQ024).
We present a ghost imaging scheme that can obtain a good pseudocolor image of black-and-white objects. The essential idea is to use a multi-wavelength thermal light source and the phase modulation pseudocolor encoding technique, which overcomes the disadvantages of other methods involved spatial filtering. Therefore, the pseudocolor ghost image achieved by this imaging scheme is better than that obtained by other methods in terms of brightness, color, and signal-to-noise ratio.
Ghost imaging (GI) is a novel and indirect optical imaging technique. In contrast to classical optical imaging, GI is obtained by correlating two light beams to reconstruct the image. Therefore, the advantages of GI with respect to classical optical imaging stems from its ability to form images without the need for a spatial-resolving detector placed near the objects. Consequently, GI is a good imaging scheme for imaging objects that are located in an optically harsh environment, e.g. turbid medium, [1] scattering media, [2] and atmospheric turbulence.[3– 5]
In practice, there are many black-and-white objects whose corresponding images are very low, which cannot satisfy practical application. Making the image of black-and-white objects appear as a colored image is a good way to improve the image quality. Previous work has shown that a colored image can be obtained by GI with spatial filtering.[6] However, this is limited by the spatial filtering and the image quality (including brightness, color, and signal-to-noise ratio) is not very good. We now ask a question: how can we obtain the black-and-white objects' colored ghost image with high image quality?
In this paper, we theoretically obtain a colored image of black-and-white objects by using a multi-wavelength thermal light source and the phase modulation pseudocolor encoding technique. The GI can be achieved by the quantum and thermal light sources. Quantum GI utilizes the biphoton source generated by spontaneous parametric down conversion.[7] In contrast to the quantum case, thermal GI is obtained by using two correlated thermal light beams that are obtained by means of a rotating ground glass plane (RGGP) and a beam splitter (BS).[8, 9] In Ref. [10], the authors showed that thermal GI can be obtained by a multi-wavelength source, although most GI theoretical analysis and experiments were carried out for the single wavelength source. Therefore, some methods of information optics can be applied to the thermal GI, such as the pseudocolor encoding technique through phase modulation.[11]
The phase modulation pseudocolor encoding technique, which can overcome the disadvantages of spatial filtering, is based on the incoherent optical processing system[12] and it obtains the transformation of the spatial intensity-modulated information and the spatial wavelength-modulated information by modulating and demodulating the information. Moreover, the Fourier transform in thermal GI has been demonstrated to be effective.[13, 14]
Two light beams are needed in the GI setup: the first is the object light beam, which interacts with the object and then the transmitted light (transmissive GI) is detected by a bucket detector, the second is the reference light beam, which is directly detected by a CCD. The correlation signals between the output currents produced by the two detectors reconstruct the ghost image. We use lensless GI to complete our work, because the lens is not necessary for thermal GI.[15]
The schematic diagram of our scheme is depicted in Fig. 1. Three quasi-monochromatic lasers (i.e., red, green, and blue) first pass through the RGGP. Then, each of quasi-monochromatic lasers produces the object and reference light beams by means of a 50:50 beam splitter. It is noted that the RGGP is only used to produce two spatially correlated and incoherent light fields in degenerate-wavelength GI.[8, 16] However, this method is not suitable for nondegenerate-wavelength GI.
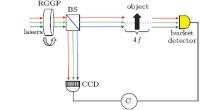 | Fig. 1. Setup for phase modulation pseudocolor encoding GI. RGGP: rotating ground glass plate. BS: beam splitter. |
The object needs to be treated before imaging based on the process of pseudocolor encoding through phase modulation. First, an object with density Da(x, y) needs to be sampled by a Ronchi grating. The transmittance of the Ronchi grating is given by[11]
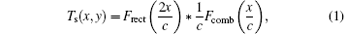
where c is the cycle of Ronchi grating, Frect and Fcomb represent the rectangular function and the comb function, respectively. The Ronchi grating object and a film are added together to be evenly exposed by the white light. The density distribution of the film after sampling is given by
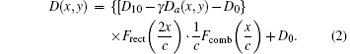
Here D0 is the fog density of the film, D10 is a constant that depends on the exposure condition, and γ is the film' s contrast coefficient. Thus, we obtain a rectangular series grating whose density can be expressed as
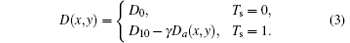
Then, through the bleaching process, we obtain a film Whose optical path difference is approximately proportional to the film’ s density, i.e.
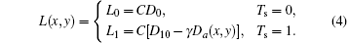
The film’ s amplitude transmittance can be expressed as
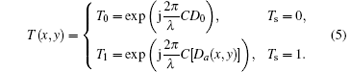
Thus, we obtain the amplitude transmittance of the phase grating
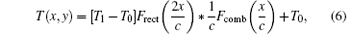
where T0 = exp(jϕ 0), T1 = exp(jϕ 1).
Third, the phase grating is placed at the input plane P1 (Fig. 2). Moreover, the light intensity of a single wavelength light is assumed as A(λ ). Thus, the complex amplitude distribution at the spectrum plane P2 can be expressed as
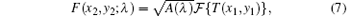
where x2 = λ fξ , y2 = λ fη , ξ and η are the spatial frequency coordinates. By substituting Eq. (6) into Eq. (7), and after some calculations, we obtain the zeroth-order and the m-th order complex amplitude distribution at the output plane P3
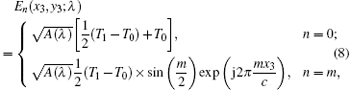
where m = ± 1, ± 3, ± 5, … . Thus, we obtain the modulated object beam whose intensity depends on the optical path difference Δ d and λ , i.e.
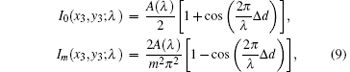
where Δ d = L1 – L0.
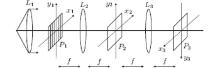 | Fig. 2. The incoherent optical processing system (4f system). The two lenses, L2 and L3, have identical focal lengths (i.e., f). |
Since the phase modulation pseudocolor encoding GI is achieved by a composite light source (i.e. three primary colors), the object beam can be expressed as
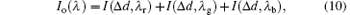
with
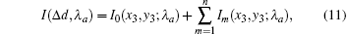
where a = r, g, b, λ a represent the wavelength of the red, green, and blue. For simplicity, the zeroth-order output can be considered in the following analysis.
The light fields detected by the bucket detector and CCD can be, respectively, expressed as
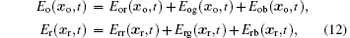
where[8]
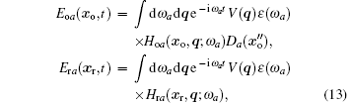
and
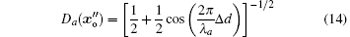
is the transmittance of the phase grating. The lasers’ incident on the front surface of the RGGP are considered to be plane waves with spectra expressed as ε (ω ). V(q) is a random spatial mask function, and we assume that it is taken to be the same for λ r, λ g, and λ b. Two Huygens– Fresnel Green' s functions Ho and Hr describe the light' s propagation between the beam splitter and the two detectors. x and q are transverse position and wave vectors, respectively. x, y represent the coordinates in the plane of the 4f system.
By measuring the intensity correlation function, we obtain the ghost image[17, 18]
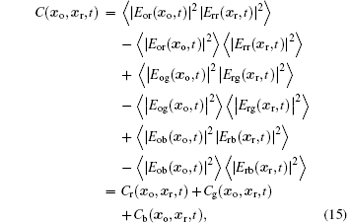
where
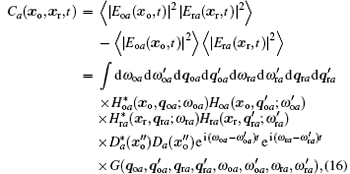
and

is the correlation function. For simplicity, we subtract the background term by several methods.[19, 20] The correlation function (16) can be rewritten as
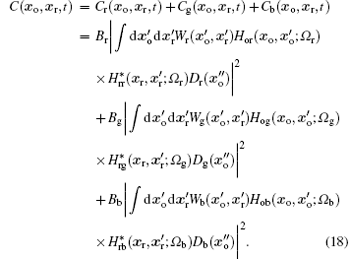
Here: Ba = IoaIra with Ia = ⟨ | ∫ dω aε (ω a)e– iω at| 2⟩ being the product of the average intensities of the two beams of the light. 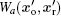
From Eq. (18), we can see that the phase modulation pseudocolor encoding GI with three independent light sources yields three modulated monochromatic ghost images that are added together to form one ghost image. Since the GI needs two light beams, the color of the ghost image is a composite color that depends on the object and reference beams. According to the above analysis, the two light beams have the same light wavelength. Thus, the color of each ghost image is a monochromatic image that is dependent on the wavelength of the light source (see in Ba).[21] When the pseudocolor ghost image is achieved by more light sources, a more colorful ghost image can be obtained. As the GI is achieved by the zero-order diffraction output, the relationship between the intensity of each monochromatic ghost image and the optical path difference Δ d is shown in Fig. 3.
Theoretically, all of the visible light can be used in this imaging scheme because the phase modulation pseudocolor encoding does not involve the spatial filtering. Thus, the signal-to-noise ratio (SNR) and brightness of pseudocolor ghost image can be increased by increasing the number of the monochromatic light source. We will next show this. Many previous works[10, 20, 22– 25] have studied the SNR of GI with a single wavelength source and multi-wavelength source. We assume that the pseudocolor ghost image obtained by the i-th wavelength can be expressed as
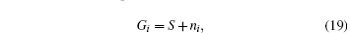
where ni is the noise of the i-th wavelength source. The noise of each wavelength source is generally different. S is a signal that is the same for all wavelength sources. Thus, the total output ghost image can be expressed as

where E{ · } is the average. Furthermore, there is no correlation between different noises, i.e.,
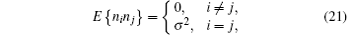
where σ represents the noise variance. Since the noise is completely random, E{ ni} = 0. Thus, we obtain
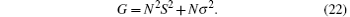
Therefore, the SNR of a ghost image with N wavelength source can be expressed as

where (SNR)s is the SNR of ghost image with single wavelength source. Equation (23) shows that the SNR of the ghost image is proportional to the number of the wavelength. Thus, the image quality (SNR) of the pseudocolor ghost image obtained by the phase modulation involving N (N ≥ 2) wavelengths is better than that obtained by the real-time pseudocolor coding involving only two wavelengths.
In summary, a good pseudocolor ghost image of black-and-white objects has been theoretically obtained by the multi-wavelength thermal light source and the phase modulation pseudocolor encoding technique. The pseudocolor ghost image obtained by this imaging scheme is brighter and more colorful than that obtained by the real-time pseudocolor encoding technique. At the same time, it has a higher signal-to-noise ratio because the phase modulation pseudocolor encoding does not involve spatial filtering. Moreover, this imaging scheme is also effective for computational ghost imaging.[26] Other methods (including time-saving[27– 29] and enhancement of the signal-to-noise ratio[30, 31]) can be combined with our imaging scheme to further improve the image quality of the pseudocolor ghost image of black-and-white objects.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 | [Cited within:1] |
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|



