Cite this Article
Tan Zhi-Zhong†. Recursion-transform approach to compute the resistance of a resistor network with an arbitrary boundary. Chinese Physics B, 2014, 24(2): 020503  
Permissions
Recursion-transform approach to compute the resistance of a resistor network with an arbitrary boundary
Tan Zhi-Zhong†
Department of Physics, Nantong University, Nantong 226019, China

Corresponding author. E-mail: tanz@ntu.edu.cn, tanzzh@163.com

Abstract

We consider a profound problem of two-point resistance in the resistor network with a null resistor edge and an arbitrary boundary, which has not been solved before because the Green’s function technique and the Laplacian matrix approach are invalid in this case. Looking for the exact solutions of resistance is important but difficult in the case of the arbitrary boundary since the boundary is a wall or trap which affects the behavior of a finite network. In this paper, we give a general resistance formula that is composed of a single summation by using the recursion-transform method. Meanwhile, several interesting results are derived by the general formula. Further, the current distribution is given explicitly as a byproduct of the method.

Keyword: 05.50.+q; 84.30.Bv; 01.55.+b; 02.10.Yn; exact solution; resistor network; matrix equation; recursion-transform; boundary conditions
1. Introduction

The computation of two-point resistances in networks is a classical problem in electric circuit theory and graph theory.[1– 5] Nowadays, research on the resistor network is expanded into the basic model in the field of science and engineering.[6– 20] A lot of abstract and complex scientific problems have been solved by modeling resistor networks[11– 20] since the German scientist Kirchhoff (1824– 1887) founded the node current law and the circuit voltage law in 1845. The previous research on resistor networks has focused on the infinite networks due to the poor technology, [3] and little attention has been paid to finite networks, even though the latter occur in real life. Looking for the exact solution of resistance between any two nodes in a resistor network in the finite case is important but difficult. The construction of, and research on, the models of resistor networks therefore are of significance in theory and application.

In 2000, Cserti[3] evaluated a two-point resistance of a resistor network by using the lattice Green’ s function which is confined to regular lattices of infinite size. In 2004, Wu[4] formulated a different approach and derived an expression for the two-point resistance in arbitrary finite and infinite lattices with a normative boundary (such as free, periodic boundary, etc.) in terms of the eigenvalues and eigenvectors of the Laplacian matrix. Laplacian analysis has also been extended to impedance networks after a slight modification of the formulation in Ref. [5], and recently it has been applied to a cobweb network.[8] However, the Laplacian approach cannot be applied to the matrix with arbitrary elements. The actual computation depends crucially on the geometry of the network and, for nonregular lattices such as a resistor network with arbitrary boundaries, it is incapable of solving the eigenvalue problem. However, the boundary condition is important because it is a real case occurring in real life. The boundary is a wall or trap which affects the behavior of a finite network.

Recently we[9, 10] proposed a new method to calculate the two-point resistance in a network. We used this method to compute the equivalent resistance, which relies on just one matrix along one direction, and expressed the exact resistance by single summation. Using the description in Refs. [9] and [10] we refer to this method as the recursion-transform approach (or the RT method). When just one boundary or a pair of opposite boundaries are arbitrary, the RT method is still valid for the computation of resistance. The RT method has been used to solve many problems of the resistor network. For example, in 2013 a cobweb model and a conjecture were proposed by us, [9, 10] soon afterwards a globe network was solved.[11] Almost at the same time, the cobweb conjecture was solved in Ref. [12]. Very recently a cobweb network with 2r boundary was solved.[13]

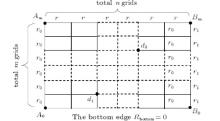
We consider an m× n resistor network with resistances r and r0 in the respective horizontal and vertical directions, except for the arbitrary right edge and the bottom boundary, as shown in Fig. 1. This paper focuses on the computation of the two-point resistance between any two nodes in the resistor network with an arbitrary boundary, which has not been solved before because the Green’ s function technique and the Laplacian matrix approach are invalid in this case.

Fig. 1. An m × n resistor network with arbitrary right boundary and null resistors at the bottom. The bonds in the horizontal and vertical directions are resistors r and r0, except for the bottom and right boundaries.

The rest of this paper is organized as follows. In Section 2, we present several exact formulae of the resistance between any two nodes in a resistor network with an arbitrary boundary. In Section 3, we prove the equivalent resistance by the recursion-transform method, and test the formula by an example. In Section 4 a summary and discussion of the method and results are presented.

2. Main results

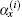
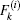
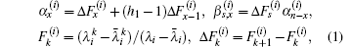
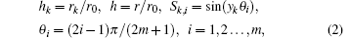
In order to facilitate the computation of the equivalent resistance of a resistor network, we define variables , , and Sk, i by

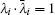
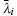
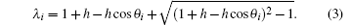
where , and λ i, are, for later uses, expressed as

We consider an m × n resistor network as shown in Fig. 1. Assume that A0 is the origin of the rectangular coordinate system, then the left edge will act as a Y axis and the bottom edge as an X axis. Denoting nodes of the network by coordinate {x, y}, the equivalent resistance between any two nodes d1 (x1, y1) and d2 (x2, y2) in the m × n resistor network can be written as

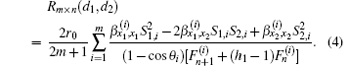
In particular, we have the following special cases.

Cases 2.1 When n → ∞ , x1, x2 → ∞ with x1 − x2 being finite, we have

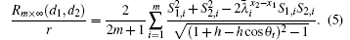
Case 2.2 When m, n → ∞ , but y1, y2, and x1 − x2 are finite, we have

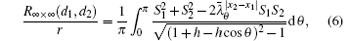
where Sk = sin(ykθ ), and .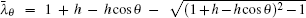

Case 2.3 When m, n → ∞ but x1 − x2 and y1 − y2 are finite, we have

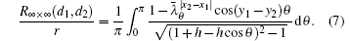
Case 2.4 When d1 = (x1, 0) is at bottom edge and d2 = (x2, m) is at top edge, we have

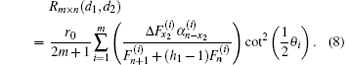
Case 2.5 When d1 and d2 are both at the left edge at d1(0, y1) and d2 (0, y2), we have

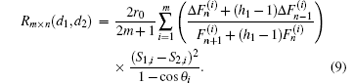
Case 2.6 When d1 and d2 are both on the left boundary, and m, n → ∞ , we have

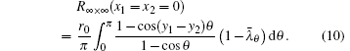
Case 2.7 When d1= (0, y1) is at the left edge and d2= (n, y2) is at the right edge, we have

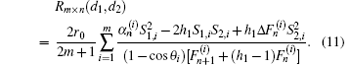
Case 2.8 When h1 = 0, we have

The general formula (4) and the above eight cases are given for the first time. From expression (4) we can deduce a lot of simple results because the r1 is an arbitrary resistor and m, n are two arbitrary natural numbers.

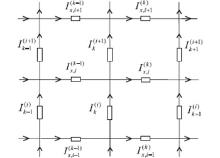
3. Matrix equation and general solution
3.1. Overall train of thought and design

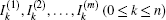
Assume that the electric current J is constant and goes from the input d1 to the output d2, as shown in Fig. 1. Denote the currents in all segments of the network as shown in Fig. 2. The resulting currents passing through all m + 1 row horizontal resistors with the same resistance of r are , respectively. The resulting currents passing through all n + 1 row vertical resistors with the same resistance of r0 are , respectively.

Fig. 2. Sub-network of resistors with marked parameters and directions of the currents.

We use Ohm’ s law to compute the resistance Rm× n (d1, d2). All of the nodes on the bottom boundary can be uniformly called O because the resistances of the bottom resistors are all zero. The voltages between two nodes O and d1, and two nodes O and d2 are, respectively,

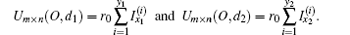
Using Ohm’ s law, we have

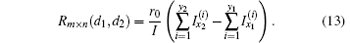
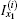
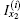
How to solve the current parameters and is the key to the problem. We are going to solve the problem by the RT method.

3.2. Modeling the matrix equation

Using Kirchhoff’ s law (KCL and KVL) to analyze the resistor network, the node current equations and the mesh voltage equations can be achieved from Fig. 2. We focus on the four rectangular meshes and nine nodes, and give the relations in the absence of an injected current,

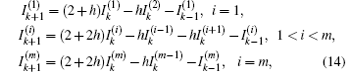
where h = r/r0 is a ratio of two resistance. Equation (14) can be written in a matrix form after considering the input and output current

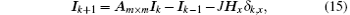
where Ik and Hx are, respectively, m × 1 column matrix, and reads

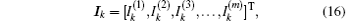
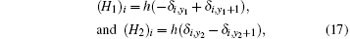
where []T denotes matrix transpose, and (Hk)i is the element of Hx with the injection of current J being at d1 (x1, y1) and the exit of current J being at d2 (x2, y2). And

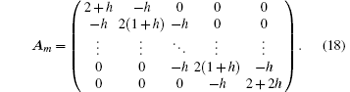
Equations (15)– (18) form the matrix equation model of the m× n resistor network.

3.3. General solution of the matrix equation

How to solve the matrix equation (15) is the key to the problem. In this section we consider the solution of Eq. (15) in the absence of an injected current, namely: J = 0. Here we rebuild a new difference equation to solve Eq. (15) indirectly. To realize the idea, first we multiply Eq. (15) from the left-hand side by m × m undetermined square matrix Pm. Thus we have

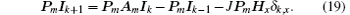
We conduct the transformation of diagonal matrix by the following identity:

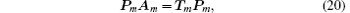
where Tm = diag(t1, t2, … , tm) is a diagonal matrix. Solving Eq. (20) we obtain

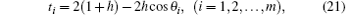
where θ i = (2i − 1)π /(2m + 1), and

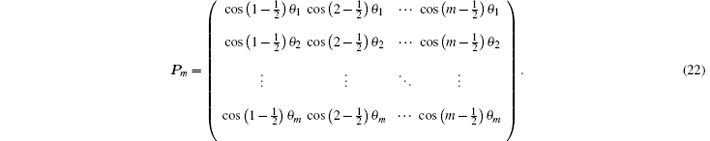
A simple calculation shows that, the new matrix Pm is invertible, with the following inverse matrix:

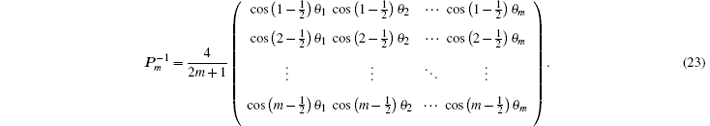
By Eqs. (19) and (20) we define

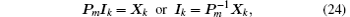
where Xm is an m × 1 column matrix, and reads

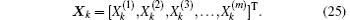
Using Eqs. (19) and (24), we obtain the equation

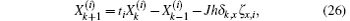
where (read ζ x1, i as ζ 1, i, ζ x2 , i as ζ 2, i)

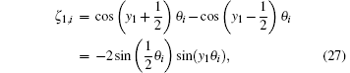
Equation (26) is much simpler than Eq. (15) because it is a linear equation that is easily derived. Suppose that λ i, 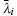are the roots of the characteristic equation for Xk, from Eq. (26) we obtain expression (3).

Next, we consider the solution of Eq. (26) when the injection of current J is at d1 (x1, y1) and the exit of current J is at d2 (x2, y2). We therefore need to consider the piecewise solution of Eq. (26) and obtain

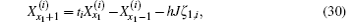
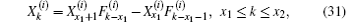
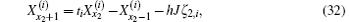
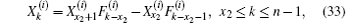
where 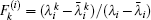is defined in Eq. (1).

3.4. General formula of the bound current

We consider the boundary conditions of the left and right edges in the network. By applying Kirchoff’ s laws (KCL and KVL) to a single mesh adjacent to each of the left and right boundaries, we obtain three matrix equations to model the boundary currents, that is,

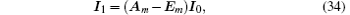
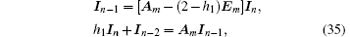
where Em is an m-dimensional unit matrix, and Am is given by Eq. (18).

Conducting the same matrix transformation as in Eq. (19), and applying Pm to Eqs. (34) and (35) on the left-hand sides, we have

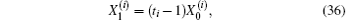
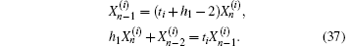
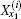
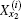
The above equations and transformations are proposals for the computation of the equivalent resistance. Next we derive two solutions of and by the above equations.

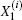
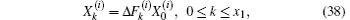
Substituting Eq. (36) into Eq. (29) to eliminate , we obtain

where is defined in Eq. (1). By Eq. (31), together with Eqs. (38) and (30), we obtain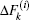

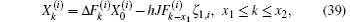
where

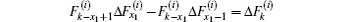
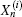
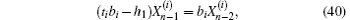
is used. Using Eq. (37) to eliminate yields

where we define bi = ti + (h1 − 2).

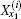
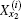
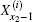
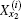
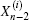
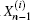
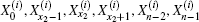
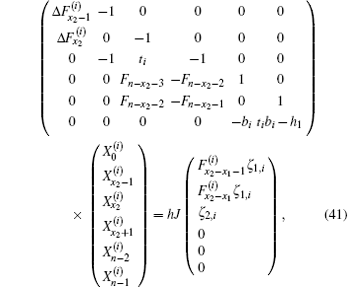
To obtain the initial conditions and needed in our resistance calculation of Eq. (13), we also need several independent equations. Since and satisfies Eq. (39), and and satisfies Eq. (33), we therefore obtain four independent equations. Together with Eqs. (32) and (40) we have six independent equations relating to the six unknowns , namely,

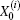
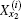
where ti = 2(1 + h) − 2hcos θ i is given by Eq. (21), and bi = ti + (h1 − 2) appearing in Eq. (40). Solving Eq. (41), we obtain after some algebra and reduction the solution of and that is needed in our process of resistance calculation,

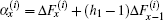
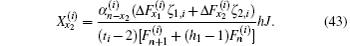
where is defined in Eq. (1) and

Substituting Eq. (42) into Eq. (38) with k = x1 yields

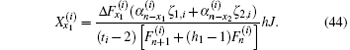
3.5. Derivation of the general formula

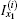
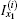
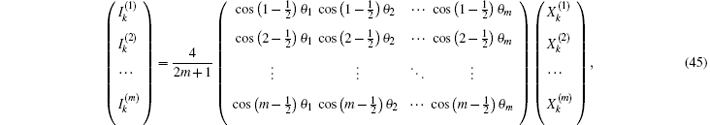
Equation (13) obviously shows the key currents and must be calculated for deducing the equivalent resistance Rm× n (d1, d2). Making use of Eqs. (23) and (24) we obtain

where k = 0, 1, 2, … , n. Taking k = x1, we therefore achieve the following equation:

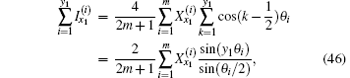
where the identity 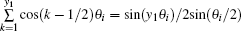is used.

Similarly, taking k = x2 in Eq. (45), we also obtain

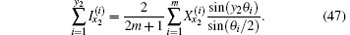
Substituting Eqs. (46) and (47) into Eq. (13) we obtain

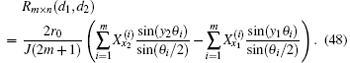
Finally, we obtain the main result (4) by further substituting 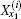and from Eqs. (44) and (43) into Eq. (48). So far the general formula (4) is proved.

3.6. Several special results

In this section we will prove several special results that were proposed in Section 1 by formula (4).

Case 3.6.1 when n → ∞ with m being finite, by Eqs. (1) and (2) we obtain

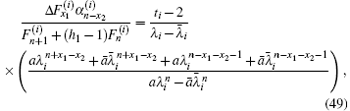
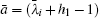
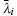
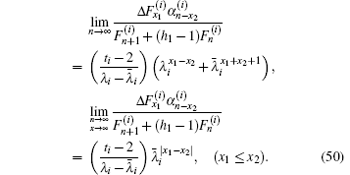
where a = (λ i + h1 − 1) and . From Eq. (3) we know that λ i > 1 > > 0, thus

Similarly, we obtain

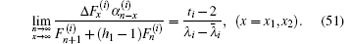
Substituting Eqs. (50) and (51) into Eq. (4), we obtain Eq. (5) after having used .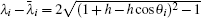

Case 3.6.2 In order to prove Eqs. (6) and (7), we need to refer an integral theory, as follows.

If θ k = (2k − 1)π /(2m + 1), we have Δ θ k = θ k + 1 − θ k = 2π /(2m + 1). In the limit of m → ∞ , we have

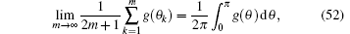
which is an identity valid for any function g(θ k). Equation (52) is prepared to prove Eqs. (6) and (7) in the following.

When m, n → ∞ , but y1, y2, and x1 − x2 are finite, making use of Eqs. (5) and (52) we immediately obtain Eq. (6).

Case 3.6.3 According to the identity transform of a trigonometric function, we have

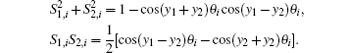
When m → ∞ and y1, y2 → ∞ , we must transform

where p, q ≪ m are integers, and (p − q) = (y1 − y2) are finite. As θ i = (2i − 1)π /(2m + 1), we have

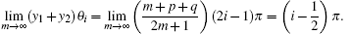
Thus

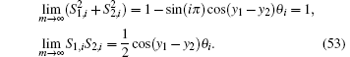
By Eqs. (5) and (53) we obtain

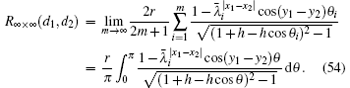
Thus equation (7) is proved.

Case 3.6.4 When d1 is at the bottom edge (x1 , 0) and d2 is at the top edge d2 (x2, m), since d1 is on the null resistor edge, we have x1 = x2, thus

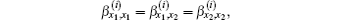
and

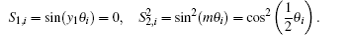
Since 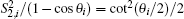, equation (4) is immediately converted into Eq. (8).

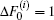
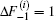
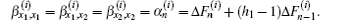
Case 3.6.5 When d1 and d2 are both on the left edge, we have x1 = x2 = 0. Since and , we have

So, by Eq. (4) we obtain Eq. (9).

Case 3.6.6 When m, n → ∞ with x1 = x2 = 0, taking limit

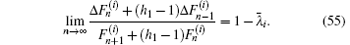
Substituting Eq. (55) into Eq. (9), and using Eqs. (52) and (53), we obtain Eq. (10).

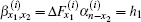
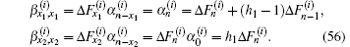
Case 3.6.7 When d1 is at the left edge (0, y1) and d2 is at the right edge (n, y2), we have x1 = 0 and x2 = n. Thus , and

Substituting Eq. (56) into Eq. (4), we obtain Eq. (11).

Case 3.6.8 When h1 = 0, we have 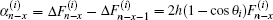, thus equation (4) immediately turns into Eq. (12).

4. Testing of a simple example

Because the main formulae are too complicated to understand, we will verify their correctness by an example.

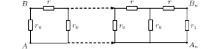
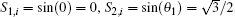
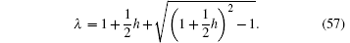
When m = 1, figure 1 degrades into a 1× n resistor network with an arbitrary right boundary, as shown in Fig. 3. When we compute the resistance between nodes A and B, then we have y1 = 0, y2 = 1. Thus by Eq. (2) we have θ i = θ 1 = π /3, and and

Fig. 3. The 1 × n resistor network with arbitrary right boundary.

From Eq. (9) we obtain the resistance

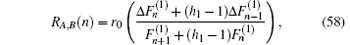
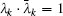
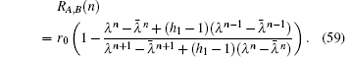
where h = r/r0, h1 = r1/r0, and . Simplifying Eq. (58) leads to

Formula (59) is fully consistent with the result in Ref. [9]. In particular, when n = 1, from Eq. (59) we have

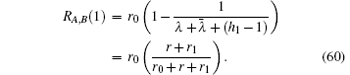
Obviously, formula (60) is completely accordant with the actual circuit. In fact, our results are bound to be perfect since all of the processes of algebra and reduction are strict and self-consistent.

5. Summary and discussion

For the explicit computation of two-point resistance, Cserti[3] evaluated the two-point resistance using the lattice Green’ s function and restricted his study to regular lattices of infinite size. In 2004, Wu[4] established a theorem to compute the equivalent resistance between two nodes in a resistor network using the Laplacian approach, and he restricted his study to a regular boundary. The arbitrary boundary is a wall or trap which affects the behavior of a finite network. When the network is of finite size and with arbitrary boundary, Green’ s function technique and the Laplacian matrix approach are both invalid.

In the present article, we solve a complicated problem of a resistor network with an arbitrary boundary by the RT method. Our results are given in the form of a single summation. This method splits the derivation into three parts. The first part is to create a recursion relation (expressed by matrix) between the current distributions on three successive vertical lines. The second part is to diagonalize the matrix relation to produce a recurrence relation involving only variables on the same transverse line. The third part is to derive a recursion relation between the current distributions on the boundary. Basically, the method reduces the problem from two dimensions to one dimension.

The RT method can be extended to impedance networks because it is formulated on Ohm’ s law and this is also applicable to impedances. In addition, the grid elements r and r0 can be either resistors or impedances, we can therefore study an m × n complex impedance network, such as

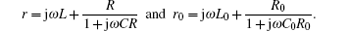
Based on the plural analysis, the formula of the equivalent impedances of the m × n RLC network with an arbitrary boundary can be obtained.

Reference
1 Kirchhoff G 1847 Ann. Phys. Chem. 148 497 DOI:10.1002/(ISSN)1521-3889 [Cited within:1]
2 Kirkpatrick S 1973 Rev. Mod. Phys. 45 574 DOI:10.1103/RevModPhys.45.574 [Cited within:1] [JCR: 44.982]
3 Cserti J 2000 Am. J. Phys. 68 896 DOI:10.1119/1.1285881 [Cited within:3] [JCR: 0.782]
4 Wu F Y 2004 J. Phys. A: Math. Gen. 37 6653 DOI:10.1088/0305-4470/37/26/004 [Cited within:2] [JCR: 1.577]
5 Tzeng W J and Wu F Y 2006 J. Phys. A: Math. Gen. 39 8579 DOI:10.1088/0305-4470/39/27/002 [Cited within:2] [JCR: 1.577]
6 Essam J W and Wu F Y 2009 J. Phys. A: Math. Theor. 42 025205 DOI:10.1088/1751-8113/42/2/025205 [Cited within:1] [JCR: 1.766]
7 Izmailian N Sh and Huang M C 2010 Phys. Rev. E 82 011125 DOI:10.1103/PhysRevE.82.011125 [Cited within:1] [JCR: 2.313]
8 Izmailian N Sh, Kenna R and Wu F Y 2014 J. Phys. A: Math. Theor. 47 035003 DOI:10.1088/1751-8113/47/3/035003 [Cited within:1] [JCR: 1.766]
9 Tan Z Z 2011 Resistance Network Model Xi’an Xidian University Press 6 216 [Cited within:4]
10 Tan Z Z, Zhou L and Yang J H 2013 J. Phys. A: Math. Theor. 46 195202 DOI:10.1088/1751-8113/46/19/195202 [Cited within:3] [JCR: 1.766]
11 Tan Z Z, Essam J W and Wu F Y 2014 Phys. Rev. E 90 012130 DOI:10.1103/PhysRevE.90.012130 [Cited within:2] [JCR: 2.313]
12 Essam J W, Tan Z Z and Wu F Y 2014 Phys. Rev. E 90 032130 DOI:10.1103/PhysRevE.90.032130 [Cited within:1] [JCR: 2.313]
13 Tan Z Z 2014 Commun. Theor. Phys. 63 36 [Cited within:1]
14 Giordano S 2005 Int. J. Circ. Theor. Appl. 33 519 DOI:10.1002/(ISSN)1097-007X [Cited within:1]
15 Izmailian N Sh and Hu C K 2007 Phys. Rev. E 76 041118 DOI:10.1103/PhysRevE.76.041118 [Cited within:1] [JCR: 2.313]
16 Keating J P, Linden N, Matthews J C F and Winter A 2007 Phys. Rev. A 76 012315 DOI:10.1103/PhysRevA.76.012315 [Cited within:1] [JCR: 3.042]
17 Izmailian N Sh and Hu C K S 2002 Phys. Rev. E 65 036103 DOI:10.1103/PhysRevE.65.036103 [Cited within:1] [JCR: 2.313]
18 Sand vik and Anders W 2012 Phys. Rev. B 85 134407 DOI:10.1103/PhysRevB.85.134407 [Cited within:1]
19 Carl P Goodrich, Andrea J Liu and Sidney R Nagel 2012 Phys. Rev. Lett. 109 095704 DOI:10.1103/PhysRevLett.109.095704 [Cited within:1] [JCR: 7.943]
20 Lu W T and Wu F Y 2001 Phys. Rev. E 63 026107 DOI:10.1103/PhysRevE.63.026107 [Cited within:2] [JCR: 2.313]