Corresponding author. E-mail: zhangjy@gzhu.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 11273009 and 11303006).
In this paper, a canonical ensemble model for black hole quantum tunneling radiation is introduced. We find that the probability distribution function is the same as the emission rate of a spherical shell in the Parikh–Wilczek tunneling framework. With this model, the probability distribution function corresponding to the emission shell system is calculated. Therefore, the concrete quantum tunneling spectrum of the Schwarzschild black hole is obtained.
Hawking radiation, which is named after the physicist Stephen Hawking who described this radiation in 1974, is a black body radiation that is predicted to be released by black holes due to the quantum effects near the event horizon. In the condition of a classical limit eβ ω ≫ 1, the Hawking radiation spectrum is[1, 2]
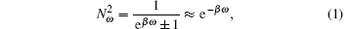
where β = 1/T = 8π M, ω is the energy of the emitted particle, T and M are the Hawking temperature and the total mass of the black hole, respectively. Hawking radiation reduces the mass and the energy of the black hole, as a result the information puzzle will arise during the emission process.
In order to solve the information puzzle, in 2000 Parikh and Wilczek came up with a semi-classical method to calculate the emission rate of particles at the event horizon of a black hole.[3– 5] The main idea is that if energy conservation is taken into account, then the emission process will be a quantum tunneling and the barrier will be determined by the self-gravitation interaction of the emission particles. In order to keep the spherical symmetry of the space time during the emission process, Parikh and Wilczek treated the tunneling particle as a spherical shell (emission shell). In this way, a corrected spectrum which is accurate to the first order approximation is given out.[6– 31] According to the Parikh– Wilczek tunneling framework, the corrected emission spectrum of a black hole is[32]

Since 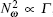
As introduced in Ref. [32], we consider the black hole as a large heat source and the emission shell as a thermodynamical system which is composed of a large number of identical particles (photons). Then we can analyze the emission shell with the cannonical ensemble theory. We suppose that the isolated system consists of black hole and emission shell, the total energy of black hole is Mc2, and the total energy of the emission shell system is E = ħ ω . By the cannonical ensemble model, we find that the probability distribution function is the same as the emission rate of the spherical shell Γ , [32]
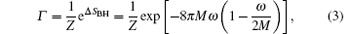
here, Z is the canonical partition function of the spherical shell system, [32]
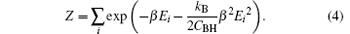
In previous study, the expression of the canonical partition function Z has not been given. In this paper, we will calculate the canonical partition function Z with the canonical ensemble model and, therefore, the formula of the quantum tunneling spectrum of the black hole Γ will be obtained.
Let us take the Schwarzschild black hole as an example.
We should choose appropriate coordinates to extend the theory of phase space in the canonical ensemble into curved space-time. We introduce the Painleve coordinates in which the singularity at the event horizon disappeared and the space-time slice is Euclidean. In this coordinate system, the three-dimensional space is flat, thus the theory of flat phase space is applicable.[33]
The line element of Schwarzschild black hole in the Painleve coordinates can be written as[33]

here

The energy and the horizon of the Schwarzschild black hole is changed by the tunneling of particles. The energy of the black hole Mc2 reduces to Mc2 − E after the particles tunnel from the black hole. The horizon of the black hole changes from ri to rf, where[34]
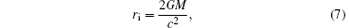
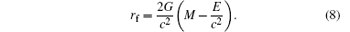
Then, the thickness of the spherical shell d is
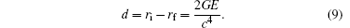
Because the shell is very thin, the volume of the emission shell in Painleve coordinates is
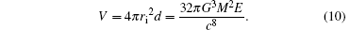
We analyze the emission spherical shell system by the semi-classical statistics. The canonical partition function Z is[35]
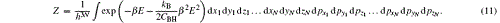
As the emission shell system consists of a vast majority of identical particles, we have
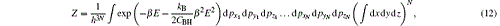
therefore
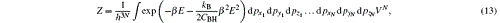
where V = ∫ dxdydz is the volume of the emission shell in Painleve coordinates, which is just the same as Eq. (10).
Compare the first order β E and the second order kB/(2CBH)β 2E2 in Eq. (13).
The Hawking temperature of the black hole is[34]
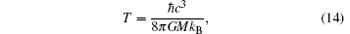
and
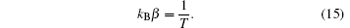
From Eqs. (14) and (15) we have
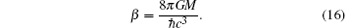
The thermal capacity of the black hole is[34]
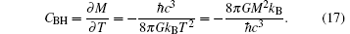
Then, divide the second order by the first one,
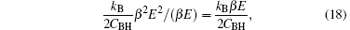
substituting Eqs. (16) and (17) into Eq. (18), we obtain
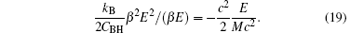
As the energy of the emission shell is more smaller than the energy of the black hole, E/(Mc2) → 0, we consider
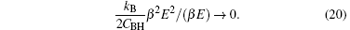
Therefore,
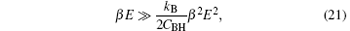
we can ignore the second order terms. As a result,

In curved space time nearby the black hole, the relation between energy and momentum of the particle satisfies the Klein– Gordon equation, [33]
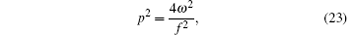
then
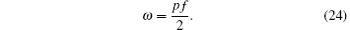
Therefore, the total energy of the emission shell is
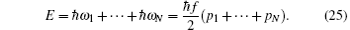
By substituting Eq. (25) into Eq. (22), the canonical partition function of the emission shell will become
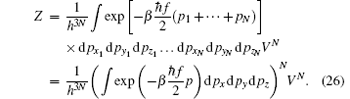
We then switch it into spherical coordinates,
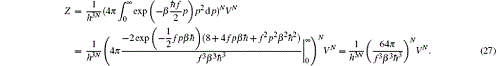
By substituting Eq. (10) into Eq. (27), we obtain
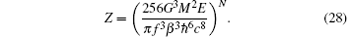
We compute the relation between the energy of the emission shell and the number of particle in the spherical system. According to thermodynamics and statistical physics, the average energy of the spherical system is[35]
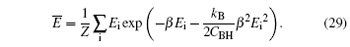
From Eq. (21), we find that the first order is much larger than the second one, therefore the second order can be ignored, [35]
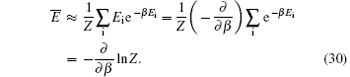
By inserting Eq. (28) into Eq. (30), we have
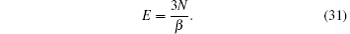
Then, the relation between the energy of the emission shell and the number of particle in the spherical system is

In the emission process, the mass of the black hole M reduces to M − E/c2, and the horizon of the black hole is determined by Eq. (7). The Schwarzschild metric in the Painleve coordinates Eq. (6) will then become

By substituting Eqs. (16), (32), and (33) into Eq. (28), we obtain the canonical partition function of the spherical shell system
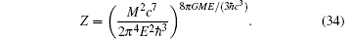
Inserting Eq. (34) and

into Eq. (3), we come out with a result that the quantum tunneling spectrum of the black hole Γ is

By transforming the expression into the Planck units G = c = ħ = 1, we have
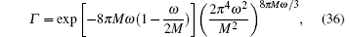
which is different from Eq. (2). This is an exact equation about Γ , M, and ω .
In summary, we will now discuss Eq. (36) in the following.
(i) The corrected emission spectrum of a black hole Eq. (2) is not an exact equation in the Parikh– Wilczek tunneling framework, there is a coefficient to be determined. In this paper, we have introduced a canonical ensemble model for the black hole quantum tunneling radiation and computed the probability distribution function of the emission shell system with this model. In this way, we have given out the coefficient of the 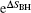
(ii) According to Eq. (36), we can see that the concrete quantum tunneling spectrum of the black hole, which is accurate to the first order approximation, is different from the black-body spectrum. This reveals that the Hawking radiation of the black hole is a non-black-body radiation. Applying this result, we are able to discuss the average radiation flux and estimate the life span of a black hole.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|


