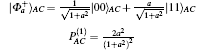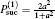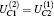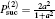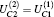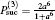Corresponding author. E-mail: na_chen@outlook.com
Project supported by the National Natural Science Foundation of China (Grant Nos. 61072067 and 61372076), the 111 Project (Grant No. B08038), the Fund from the State Key Laboratory of Integrated Services Networks (Grant No. ISN 1001004), and the Fundamental Research Funds for the Central Universities (Grant Nos. K5051301059 and K5051201021).
To realize practical wide-area quantum communication, a satellite-to-ground network with partially entangled states is developed in this paper. For efficiency and security reasons, the existing method of quantum communication in distributed wireless quantum networks with partially entangled states cannot be applied directly to the proposed quantum network. Based on this point, an efficient and secure quantum communication scheme with partially entangled states is presented. In our scheme, the source node performs teleportation only after an end-to-end entangled state has been established by entanglement swapping with partially entangled states. Thus, the security of quantum communication is guaranteed. The destination node recovers the transmitted quantum bit with the help of an auxiliary quantum bit and specially defined unitary matrices. Detailed calculations and simulation analyses show that the probability of successfully transferring a quantum bit in the presented scheme is high. In addition, the auxiliary quantum bit provides a heralded mechanism for successful communication. Based on the critical components that are presented in this article an efficient, secure, and practical wide-area quantum communication can be achieved.
Quantum information science is an emerging research field that provides various protocols for secure communication and efficient computation beyond the capabilities of its classical counterparts. Quantum communication deals with the problem of transferring quantum bits (qubits).[1– 3] It has potential applications in quantum networks, in which an unknown qubit can be transmitted directly from one node to another. However, due to the inevitable interaction of the qubits with the environment, direct transmission is not practicable for long-distance quantum communication. The most common method to transfer qubits is quantum teleportation, [4] where pre-shared entangled particle pairs are exploited to deliver qubits, which is suitable for transmission over any distance. In this paper, quantum teleportation is adopted to transfer qubits.
Existing research[5– 10] on complicated quantum communication networks is based on the maximally entangled states, ignoring the influence of long-distance quantum channel on maximally entangled states, such as the decoherence effect. However, in real world implementations, some decoherence mechanisms can take maximally entangled states to partially entangled states or mixed states. However, the latter has not been dealt with in their studies. We thus focus with great interest on quantum communication with partially entangled states.
In recent years, many efforts have been devoted to the research of quantum information processing with partially entangled states.[11– 17] However, little has been done in the study of transferring qubits in a quantum network with partially entangled states. To the best of our knowledge, a quantum communication network with partially entangled pairs was first analyzed by Yu X T, Zhang Z C and Xu J[18] (we shorten this to the YZX protocol below), whose research was based on a distributed wireless quantum communication network model and who proposed a quantum routing mechanism. Their work shows that multi-hop teleportation in distributed wireless quantum networks with partially entangled states is feasible.
The increasing amount of research available in quantum information science makes a global quantum communication network desirable. Taking technological feasibility into account, it is necessary to investigate quantum communication for wide-area networks with partially entangled states. However, directly applying the YZX protocol[18] to quantum wide-area networks achieves a low probability of successfully transferring a qubit; moreover, security and privacy cannot be guaranteed. Therefore, in this paper we further explore how to perform quantum network tasks efficiently by utilizing partially entangled states. One of our goals is to increase the probability of successfully transferring a qubit and at the same time achieve a high level of security.
This paper represents an efficient quantum communication scheme enabling qubits transmission between any two nodes in a satellite-to-ground quantum network with partially entangled states. Here, partially entangled states are directly used without any entanglement distillation strategies.[19, 20] In our scheme, the source node performs quantum teleportation only after the end-to-end entangled state has been set up between itself and the destination node. In addition, local operations to reconstruct the transmitted qubit are only needed at the destination node. Together, these guarantee the security of communication. And most of all, with the aid of an auxiliary qubit and specially defined unitary matrices, the probability of successfully transferring a qubit is significantly increased, which is demonstrated by detailed calculations and simulations. Classical information necessary for transferring qubits is transmitted through well-developed classical wireless networks. The results of this paper provide a valuable reference for convergence of the quantum and classical networks.
The rest of this paper is organized as follows. In Section 2, general concepts about entanglement swapping with partially entangled states are introduced. Section 3 describes a system model for satellite-to-ground quantum communication network. In Section 4, qubits transmission in the proposed satellite-to-ground quantum communication network is investigated in detail. Performance evaluation and simulation analyses are presented in Section 5. Finally, some conclusions are drawn in Section 6.
In this section, we introduce the basic idea of entanglement swapping with partially entangled states. Prior to which, some notations and preliminaries used throughout this paper are briefly described.
The Bell states that are used in quantum communication are generally defined as[2]
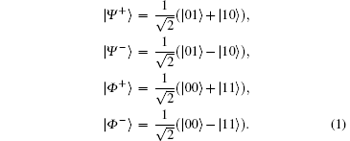
They can be transformed into each other through unitary operations defined by Pauli matrices, such as

where 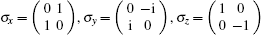
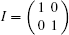
A maximally entangled state, without loss of generality, which is denoted as | Φ +⟩ , may degrade with decoherence induced by the quantum channel to

where 0 ≤ a ≤ 1. When a = 0, there is no entanglement, while for a = 1, equation (3) denotes a maximally entangled state. | 0⟩ and | 1⟩ represent the horizontal and vertical polarizations, respectively. We illustrate the entanglement degree of 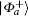
Here, let us consider the simplest case of two pairs of particles 1, 2 and 3, 4 that are initially in partially entangled states described by
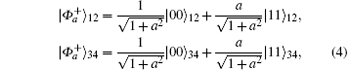
where particles 2 and 3 are in the same laboratory, particle 1 and particle 4 are in another two different laboratories. Three laboratories are spatially remote from each other. Entanglement swapping can readily be written as
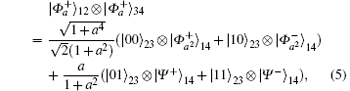
where
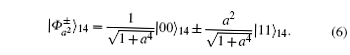
From Eq. (5) we can see that when particles 2 and 3 are projected onto one of the basis states {| 01⟩ , | 11⟩ }, the particle pair 1, 4 is projected accordingly onto one of the Bell states | Ψ ± ⟩ 14 with probability a2/(1 + a2)2. Otherwise, when particles 2 and 3 are projected onto one of the basis states {| 00⟩ , | 10⟩ }, the particle pair 1, 4 is projected as well onto one of the partially entangled states 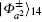
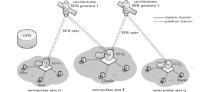
Considering that satellites provide a unique solution for distributing entangled quantum pairs in a wide-area quantum network, a satellite-to-ground quantum communication network is constructed thereby. As shown in Fig. 2, it is composed of a global position database (GPD), satellite-borne EPR generators and several metropolitan area networks. Each metropolitan area network is equipped with a powerful, high-reliability satellite ground station (SGS) and several standby devices. These SGSs constitute the interface between quantum communication terminals and the backbone network system. The main function of an SGS is to manage the quantum entangled states shared between itself and the quantum communication terminals that are inside its service area. When a quantum communication terminal inside an SGS’ s service area sends or receives qubits, then the SGS functions as an intermediate node. Each SGS can provide communication services for multiple terminals at the same time using the identity authentication mechanism. In addition, each SGS is equipped with multiple radio transceivers, which are responsible for sending and receiving classical information over classical wireless channels.
A two-tier database structure is adopted in the network. Each SGS is equipped with a local position database (LPD) to manage the information of quantum communication terminals inside its service area. An LPD can also be used to determine whether or not a specific quantum communication terminal is inside this metropolitan area. Moreover, a GPD exists in the backbone network to record the position information of all quantum communication terminals in the satellite-to-ground quantum communication network. By inquiring the GPD, one can ascertain which metropolitan area a specific quantum communication terminal resides in.
In the network shown in Fig. 2, the satellite-borne EPR generators are responsible for generating and distributing EPR pairs. Once two SGSs need to establish quantum entangled states, the specified satellite-borne EPR generator would distribute the generated EPR pairs, which are uniformly described as | Φ + ⟩ in our scheme, through quantum channels. Due to the decoherence induced by quantum channels, these two SGSs possibly share various partially entangled states with different entanglement degrees, sometimes even mixed states. But in this paper, we consider the simplest situation where two involved SGSs share a partially entangled state 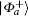
There are two kinds of communication channels for qubits transmission. Optical free-space links are generally employed as a quantum channel since they theoretically allow a much longer propagation distance for the photons due to the low absorption of the atmosphere in certain wavelength ranges. Classical data are transmitted through classical wireless channels. In Fig. 2, the dashed and solid lines represent quantum and classical wireless channels, respectively. SGSs access the GPD though classical channels, which are not depicted in Fig. 2 for simplicity.
Quantum communication terminals are quantum devices with wireless communication capabilities, they can store and process quantum information.
In the present quantum communication scheme the classical information necessary for delivering qubits is transmitted over well-developed classical wireless networks with various routing schemes.[22, 23] In order to maximize the probability of successfully transferring a qubit, the quantum path with minimum hops will be selected by referring to previous proposed quantum routing algorithms.[5, 8, 10, 18] The concrete rules of routing are not discussed in this paper.
Before discussing specific communication scenarios, we might as well make the following assumptions. Suppose that the target qubit to be transmitted is | ϕ ⟩ X = α | 0⟩ + β | 1⟩ , where | α | 2 + | β | 2 = 1. To simplify our discussion, we assume that each quantum communication terminal shares in advance enough partially entangled states, which are uniformly described as 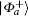
In the satellite-to-ground quantum communication network described in Section 3, we consider a circumstance in which a quantum terminal called Alice intends to transfer a qubit to another terminal (the destination node). Firstly, Alice requests the SGS that serves it, i.e. SGSO, to establish communication to the destination node. Then, SGSO would query its own LPD, i.e. LPDO, to determine whether or not the destination node is inside metropolitan area O. Accordingly, we will discuss in detail the following two communication scenarios.
Scenario 1 Alice would like to transfer a qubit to the destination node called Bob, as shown in Fig. 2.
According to previous assumptions, Bob also shares partially entangled states 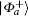

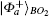
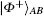
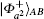
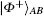
| Table 1. Relation between entanglement swapping measurement results received and local unitary operations. |
(i) The end-to-end entangled state shared between Alice and Bob is 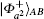
The state of the entire system before teleportation is represented by 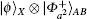
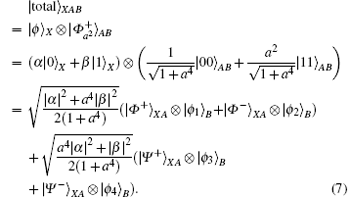
At the same time, the state of particle B with Bob turns into one of the following four possibilities
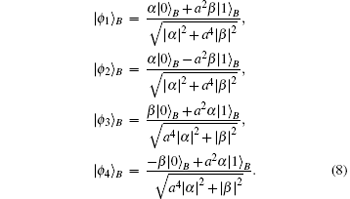
It can be seen from Eqs. (7) and (8) that particles X and A are projected onto one of the four Bell states and accordingly particle B is projected onto a state which is related to the original state of particle X. Then Alice informs Bob about her measurement results (2 bits of classical information). According to Alice’ s Bell-state measurement result, Bob performs a proper unitary operation on particle B, as shown in Table 2. After unitary operation, Bob’ s qubit evolves as follows:
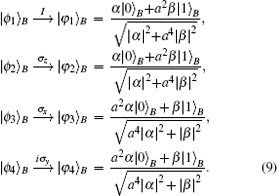
From Eq. (9), we see obviously | φ 1⟩ B = | φ 2⟩ B, | φ 3⟩ B = | φ 4⟩ B.
| Table 2. Relation between Alice’ s Bell-state measurement results and local unitary operations. |
In order to recover the target qubit | ϕ ⟩ X, Bob prepares an auxiliary qubit, which is initially described by | 0⟩ aux. If Alice’ s measurement result is 

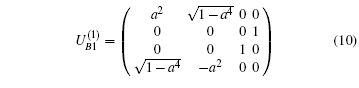
on | φ 1⟩ B| 0⟩ aux or | φ 2⟩ B| 0⟩ aux, reads

From Eq. (11), it can be seen that if Bob projects the auxiliary qubit onto the basis {| 0⟩ , | 1⟩ } and he obtains | 0⟩ aux, then his particle B definitely collapses to the target qubit | ϕ ⟩ X, thereby qubit transmission is successful. Otherwise, if he gets | 1⟩ aux, no information about | ϕ ⟩ X is obtained and the transmission fails. Apparently, the state of auxiliary qubit indicates whether or not the qubit transmission is successful, which is a heralded mechanism.
In another case, when Alice’ s measurement result is 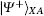
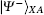
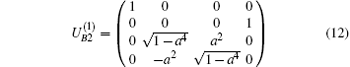
on | φ 3⟩ B| 0⟩ aux and | φ 4⟩ B| 0⟩ aux, reads
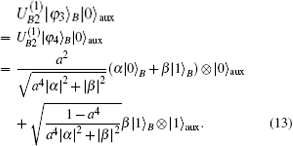
After projecting the auxiliary qubit onto basis {| 0⟩ , | 1⟩ }, qubit transmission is successful only when Bob obtains | 0⟩ aux. In the same way, the state of auxiliary qubit shows if the qubit transmission is successful.
Based on the above analyses, when Alice and Bob share 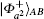
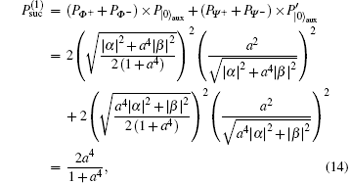
where, based on Eqs. (7), (11), and (13), we make the following denotations
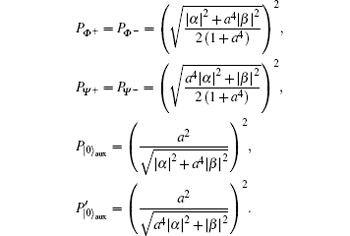
(ii) The end-to-end entangled state shared between Alice and Bob is 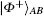
This case corresponds to teleportation with a maximally entangled state, which is a deterministic protocol. Hence, the probability of successfully transferring the target qubit | ϕ ⟩ X is 1, that is 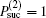
From the above discussion we can see that in Scenario 1 the probability of successfully transferring a qubit from Alice to Bob reads
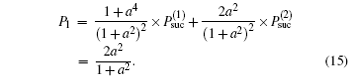
Scenario 2 Alice would like to transfer a qubit to the destination node called Charlie, as shown in Fig. 2.
After querying LPDO, SGSO learns that Charlie is not inside metropolitan area O, it then proceeds to inquire the GPD to determine which metropolitan area Charlie resides in. The GPD will respond to SGSO that Charlie is inside metropolitan area P. After applying a quantum routing protocol, each involved node will be informed that the selected quantum path is Alice → SGSO → SGSP → Charlie. Then SGSO asks the satellite-borne EPR generator 1 to set up an entangled state between SGSO and SGSP. Afterwards, the satellite-borne EPR generator 1 will distribute an EPR pair | Φ + ⟩ by sending one particle of it to SGSO and sending the other particle to SGSP. Due to the decoherence effect induced by the quantum channel, SGSO and SGSP finally share a partially entangled state denoted as

After SGSO’ s entanglement swapping, as similarly expressed by Eq. (5), and SGSP’ s unitary operations, according to Table 1, the possible entangled states shared between Alice and SGSP can be expressed as follows:
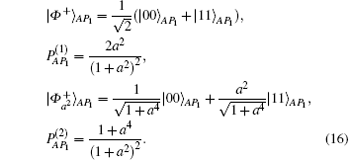
Then, after SGSP’ s entanglement swapping and Charlie’ s unitary operations, the possible end-to-end entangled states shared between Alice and Charlie and corresponding probabilities are given by the first column in Table 3. Upon receiving the notification from Charlie that the end-to-end entangled state is ready, Alice will transfer the target qubit | ϕ ⟩ X by quantum teleportation. Analogous to the analyses in Scenario 1, the critical ingredients referring to the follow-up target qubit recovery in quantum teleportation are listed in Table 3. When performing quantum teleportation, Alice’ s possible measurement results for particles X and A are described by the second column. The third column represents Charlie’ s unitary operations implemented on | φ ⟩ C| 0⟩ aux to recover the target qubit, and the last column in Table 3 shows the probabilities of successful teleportation.
| Table 3. Possible end-to-end entangled states shared between Alice and Charlie, and the follow-up target qubit recovery operations in Scenario 2. |
where,
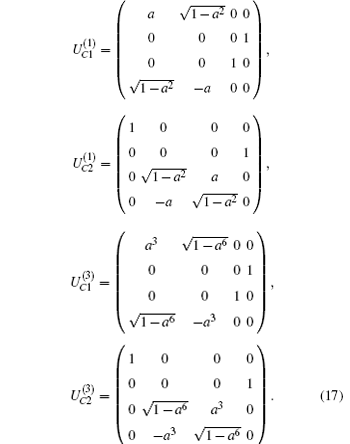
In Scenario 2, the probability of successfully transferring a qubit from Alice to Charlie reads
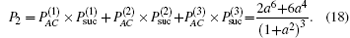
If the destination node is farther apart from the source node, then many more satellite-borne EPR generators are needed. For example, Alice would like to transfer a qubit to David, as shown in Fig. 2. By successively inquiring LPDO and the GPD, SGSO learns that David is inside the metropolitan area Q. After applying a quantum routing algorithm, each involved node will be informed that the selected quantum path is Alice → SGSO → SGSP → SGSQ → David. Then, SGSO requests the satellite-borne EPR generator 1 to set up an entangled state between SGSO and SGSP. Similarly, at the request of SGSP, the satellite-borne EPR generator 2 will distribute an EPR pair | Φ + ⟩ to SGSP and SGSQ as well. Due to the decoherence effect, the partially entangled state shared between SGSO and SGSP is
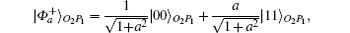
similarly SGSP and SGSQ share
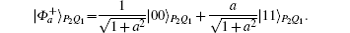
After sequential entanglement swapping performed by each intermediate node and proper unitary operations implemented by its next-hop node on the selected quantum path, the end-to-end entangled state shared between Alice and David has been established. At last, Alice transfers the target qubit | ϕ ⟩ X by quantum teleportation and David recovers it with the help of the auxiliary qubit and special unitary matrices. Detailed mathematical expressions describing the qubit transmission process are analogous to those mentioned in the two scenarios given above. The probability of successfully transferring a qubit from Alice to David reads
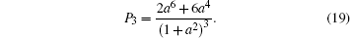
Similar analyses can be applied to quantum communication scenarios involving more nodes. In this way, two geographically distant networks can be connected together. The realization of a worldwide quantum network will be possible with the help of satellites.
In this section, the performance of the satellite-to-ground quantum communication network with partially entangled states is analyzed. Compared with quantum networks[5– 10] based on maximally entangled states, the scheme proposed here takes the influence of quantum channel on maximally entangled states into consideration. Therefore, this scheme will be more suitable for practical implementations. Though based on partially entangled states, YZX protocol[18] cannot be applied to the satellite-to-ground quantum communication network described in Section 3 because of its security flaws and the low probability of successfully transferring a qubit. However, neither of these problems exists in our quantum communication scheme.
The principle of the YZX protocol[18] is to perform teleportation hop by hop from the source to its destination. This is based on the idea that a qubit may be transferred successfully if a balanced sequence of | Φ ± ⟩ and | Ψ ± ⟩ is obtained.[14] Assume that the number of nodes on a selected quantum path is N (N > 3). It is possible that on a certain intermediate node labelled node n (n < N) a balanced sequence of | Φ ± ⟩ and | Ψ ± ⟩ is obtained. In this situation, if node n is compromised, then the target qubit will be exposed. While in our scheme, the quantum teleportation will be performed by the source, so as to transfer the target qubit, only after the end-to-end entangled state has been shared between the source and the destination has been set up. In this way, the communication security is guaranteed.
When YZX protocol[18] is applied to the satellite-to-ground quantum communication network, it gains a low probability of successfully transferring a qubit. However, in our scheme, an auxiliary qubit and special unitary matrices similar to expressions in Eqs. (10), (12), and (17), are utilized by the destination to recover the target qubit. Such ingenious strategies lead to an increase in communication efficiency. In addition, the auxiliary qubit provides a heralded mechanism for successful qubit transmission. The probabilities of successfully transferring a qubit in quantum paths with 3 nodes, 4 nodes, and 5 nodes are given by Eqs. (15), (18), and (19), respectively. Similar to the analyses presented in Section 4, when there are 6 nodes on the selected quantum path, the probability of successfully transferring a qubit is written as
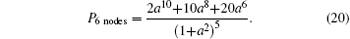
When 7 nodes exist on the selected quantum path, the success probability reads

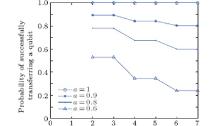
The probabilities of successfully transferring a qubit as discussed above are depicted in Fig. 3. According to the entanglement degree that is shown as Fig. 1, we take entanglement indicators a = 1, a = 0.9, a = 0.8, and a = 0.6 as examples. From Fig. 3, first of all we can see that when a = 1, the probability of successfully transferring a qubit equals 1, regardless of the number of nodes involved, which coincides with the quantum communication with maximally entangled states. Secondly, for a specific quantum path, with the decrease of entanglement degree, the probability of successfully transferring a qubit is reduced. Furthermore, for a constant entanglement degree, the probability of successfully transferring a qubit is trending downward along with the increasing number of nodes. But we need not be too concerned about this point because only a small number of satellites are needed to achieve global quantum communication.
In Fig. 4 the blue solid lines represent the probabilities of successfully transferring a qubit in the proposed scheme and the red dashed lines correspond to the success probabilities of YZX protocol.[18] Entanglement indicators a = 0.9 and a = 0.8 are taken as examples. From the simulation results shown in Fig. 4, it can be seen that when YZX protocol[18] is applied to satellite-to-ground quantum communication network, its efficiency is significantly lower than that of our scheme.
The probability of successfully transferring a qubit on a quantum path with two nodes is also plotted in Figs. 3 and 4, although it is not discussed in the constructed satellite-to-ground quantum communication network. This situation will appear when the proposed scheme is applied to a distributed quantum communication network.
In this paper, a satellite-to-ground quantum communication network is constructed and, based on this communication scenario, an efficient and secure quantum communication scheme with partially entangled states is presented. We have solved the problem that the existing method of quantum communication in distributed wireless quantum networks with partially entangled states cannot be applied directly to wide-area quantum networks because of its security flaws and low efficiency. In the proposed scheme, end-to-end entangled states are set up by sequential entanglement swapping with partially entangled states; afterwards, the source node performs teleportation to transfer qubits. In this way the security of the quantum communication is guaranteed. When the destination node recovers the transmitted qubits, the auxiliary qubit and specially defined unitary matrices are utilized. Such ingenious strategies increase the probability of successfully transferring a qubit, which has been shown in detailed calculations and simulation analyses. Moreover, the auxiliary qubit provides a heralded mechanism for successful communication. In the proposed scheme, classical information necessary for qubits transmission is transferred through well-developed classical wireless networks. The results of this paper provide a valuable reference for the convergence of quantum and classical networks.
Considering the time complexity of establishing end-to-end entangled states caused by sequential entanglement swapping, it can be performed from both ends to the middle on a specific quantum path. Thus the communication delay in the proposed scheme will be reduced.
Finally, we would like to emphasize that, for the sake of simple analysis, we have considered an ideal situation in which all of the quantum channels are assumed to possess the same entanglement. But when it comes to more realistic settings this precondition is difficult to fulfill and various changes to the quantum channels will occur; for example, decoherence possibly leads to mixed state channels. Currently, no research on teleportation and entanglement swapping with various entanglement is yet available. Actually, we have tested some channels with different entanglements and obtained no better performance. We are now devoting ourselves to a generalized wide-area quantum communication network in which irregular entangled states, imperfect measurements, and imperfect unitary operations are taken into consideration.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|