Nanometer-size semiconductor heterostructures with controlled thickness and relatively sharp interfaces are the outcome of rapid progress in crystal growth and fabrication methods. The study of such heterostructures has been a subject of intense research, both theoretically and experimentally.^{[1– 12]} Quantum rings (QRs) are self-organized nanometric semiconductors like quantum dots.^[13] Using external static fields, the control of a two-electron quantum dot has been realized experimentally^[14] and studied theoretically.^{[15– 19]} A quantum dot is transformed to QR when the density is concentrated over a certain radial distance from the dot center. It has been demonstrated experimentally^[20] that the quantum states of QRs can be tuned by electric fields and the energy structure of two-electron QRs has also been studied theoretically.^{[21– 23]}

Due to their rich electronic, magnetic, and optical properties, ^{[24– 31]} quantum rings have been studied experimentally. As a member of artificial microsystems, QRs have a unique feature: the Ahronov– Bohm effect.^{[32– 34]} Various methods, such as model Hamiltonian, ^{[35– 37]} exact diagonalization, ^{[38– 40]} Monte-Carlo calculations, ^{[37, 38]} and density functional theory, ^{[41– 44]} have been used to investigate theoretically many-electron QRs. Accurate numerical calculations on two-electron QRs have also been reported.^[45] Just as quantum dots, QRs play a very important role in nanoelectronic technology and micro-devices.^[46] Hong and coworkers^{[47, 48]} have shown the effect of external fields and impurities on the spectrum and persistent currents of two-electron QRs. One can investigate the control of physical properties of QRs using an external adjustable static electric field. We have studied in detail the effect of external static field on the dynamics of two-electron QR using three different types of short pulses: square, sine-square, and secant-hyperbolic pulse. Furthermore, the variation of transition probability with electric field, intensity, and frequency of the laser pulses and radius of the ring has been reported.

The time-dependent Schrö dinger equation for two electrons in a QR of radius R, in atomic units, in the presence of static and time-dependent fields can be written as

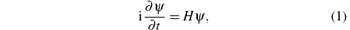
where

is the Hamiltonian of the system, E_s is the static electric field,

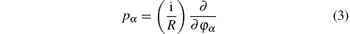
is the momentum operator associated with the electron α and φ _α is its angle around the ring circle. Atomic units have been considered where ħ = m = e = 1. The second term (operator u^{− 1}) on the right-hand side of Eq.  (1) represents the Coulomb interaction between the electrons where u is the interelectronic distance given by:^[49]

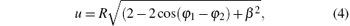
where β is a dimensionless parameter, β = d/R, d is introduced in the interaction term to compensate for the effect of the finite thickness of the QR. In addition, it removes the singularity and avoids divergence. The third term on the right-hand side of Eq.  (2) represents the interaction of the system with the external static electric field and has the form:

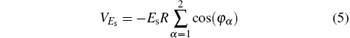
and V_int is the interaction energy of the QR under the action of short pulses given by

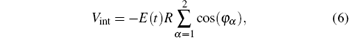
where E(t) is the electric field of the laser given by

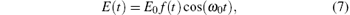
f(t) is the envelope of the short laser pulse used.

To study the effect of pulse shape on a two-electron QR system, three different pulse shapes: square (sq), sine-square (ss), and secant-hyperbolic (sh), have been used, whose envelopes are given by

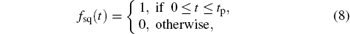
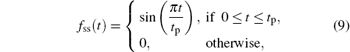
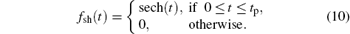
It is difficult to solve Eq.  (1) analytically, hence the equation is solved by separating the Hamiltonian into the center of mass and the relative coordinates of the electrons.

So in terms of center of mass (CM) coordinate φ _CM = (φ ₁ + φ ₂)/2 and the relative coordinate φ _r = φ ₁ − φ ₂, the Hamiltonian can be written as^{[49, 50]}

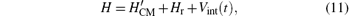
where H′ _CM and H_r are CM and relative Hamiltonian, respectively, as defined below.

We understand that the external fields only affect the CM motion. Hence, relative coordinates are hardly affected by the electric fields. Moreover, if the positions of the electrons φ ₁ and φ ₂ are such that (φ ₁ – φ ₂)/2 → 0 , then the effect of electric field is only taken to be associated with the center-of-mass motion, where

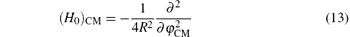
is the Hamiltonian of the CM system without electric field having energy eigenvalues as

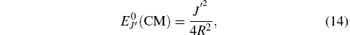
where J′ is the total angular momentum associated with the CM coordinate, and the eigenfunctions as

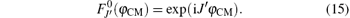
In Eq.  (12), V_CM is given below

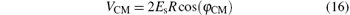
and V_int is defined as

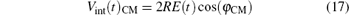
and in Eq.  (11), H_r is given by

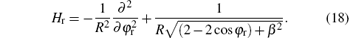
Now, having separated CM and relative motion components, we can find the total energy and the associated wavefunctions as

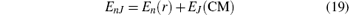
and

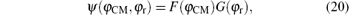
respectively.

E_n(r), G(φ _r) are eigenvalues and eigenfunctions of the Hamiltonian of the relative coordinates given by Eq.  (18), and E_J(CM), F(φ _CM) are eigenvalues and eigenfunctions of the time-independent Hamiltonian of the CM coordinates, i.e. H_CM given in Eq.  (21).

Let

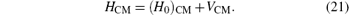
There have been few studies to solve time-independent Schrö dinger equations for CM and relative coordinates as given below

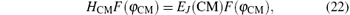
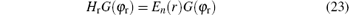
analytically.^{[17, 18]} But, here we have solved these two equations numerically by nine-point finite difference method to obtain the energy eigenvalues E_J(CM) and E_n(r), and the corresponding eigenfunctions. The energy eigenvalues and the eigenfunctions thus obtained have been used to solve the time-dependent Schrö dinger equation for two-electron QR in short pulses. As mentioned earlier, and also by others, ^{[51, 52]} the short pulses will influence only the CM motion.

Having obtained F(φ _CM), G(φ _r) and the corresponding energies, the solution of Eq.  (1) can be written as

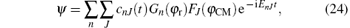
where c_nJ(t) are the time-dependent transition amplitudes. By substituting Eq.  (24) into Eq.  (1), we get a set of first-order coupled differential equation for c_nJ’ s. The resulting equation has been solved numerically by the fourth-order Runge– Kutta method. Finally, the transition probability of finding the system in the (nJ)-th state from the ground state, at time t is given by

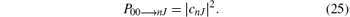
Consider a two-electron quantum ring system with applied external static electric field and short laser pulses. For all calculations other than where ring size effect has been shown, the radius of the ring, R, is taken to be 100  a.u. The laser pulses used for interaction are defined in Eqs.  (8)– (10). The duration of pulses for all three cases are the same. In order to solve Eq.  (1), ψ , the total wavefunction is taken as given by Eq.  (24), for which the time-independent wavefunctions G_n(φ _r) and F_J(φ _CM) are required. These wavefunctions have been evaluated by solving the time-independent Schrö dinger equations for relative and CM motions, respectively. Thus, the energy levels and wavefunctions so obtained include the effect of the static field. Although the states calculated are singlet as well as triplet, we have focused on the dynamics of excited singlet states.

In the numerical calculations of the dynamics of a two-electron QR system, the variation of transition probability from ground state to excited singlet states has been studied by showing the effect of laser parameters: intensity, I, and frequency, ħ ω _e; external static electric field, E_s, and radius of the ring, R. The effect of pulse shape has also been studied.

Figure  1 shows the variation of energy difference between states: E₁₁– E₀₄, E₂₁– E₀₂, E₂₁– E₀₃, with the static electric field, in the two-electron QR (where the symbols are defined in the theory section given by Eq.  (19)). The energy difference decreases with an increase in the external static electric field as the energy levels get shifted because of the Stark effect. For the sake of clarity, we have shown only a few states.

Fig.  1.

	Figure Option ViewDownloadNew Window
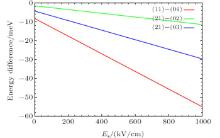	Fig.  1. Variation of energy difference of states in a two-electron QR system with external static electric field for the transitions: (11)– (04), (21)– (02), and (21)– (03).

The dynamics of the system in short pulses of different shapes are shown in Figs.  2– 4. In Fig.  2, we present the variation of transition probability from ground state to various excited states with time. The parameters used are: static electric field, E_s = 80  kV/cm, intensity of laser beam I = 8 × 10¹²  W/cm², duration of pulse t_p = 20  fs. In all of the cases we have taken the convergence parameter, d = 0.2 and ω ₀ = E₀₁ – E₀₀, i.e., one photon process. When the short laser pulse used is secant-hyperbolic (Fig.  2(c)), the transition probability from ground state to the first excited state is maximum being 0.573, followed by the transition from the ground state to the second excited state (0.254). The “ survival probability” , i.e., the ground state probability, is 0.134 followed by the ground state to the third excited state 0.036. The dynamics change drastically when the shape of the laser pulse is changed. When the sine-square pulse is used, the probability is maximum for the transition from the ground state to the second excited state 0.483, followed by the ground state to the first excited and then from the ground state to the third excited state: 0.233 and 0.203, respectively. The survival probability is 0.047, as shown in Fig.  2(b). Figure  2(a) shows the transition probability when the pulse is square in shape. As is evident from the figure, the probabilities are quite different from the above two types of pulse shapes used. The transition probability is maximum from the ground state to the third excited state (0.288), followed by the ground state to the first excited state (0.238) and the ground state to the fourth excited state (0.202). The survival probability is 0.080. Thus, one can clearly see the change in the dynamics when pulse shape of the laser is changed. Pulse shape effects on the dynamics of quantum heterostructures have recently been studied.^[53] The square, sine-square, and secant-hyperbolic pulses are of quite some importance in manipulating the optical response of such a system.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Variation of transition probability with time in a two-electron QR: (a) square pulse, (b) sine-pulse, and (c) secant hyperbalic pulse. The various physical parameters used are: Es = 80  kV/cm, I = 8 × 1012  W/cm2, R = 100  a.u., and tp = 50 fs.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Variation of transition probability with time in a two-electron QR: (a) square pulse, (b) sine square pulse, and (c) secant hyperbolic pulse. The various other parameters used are Es = 80  kV/cm, I = 8 × 1011  W/cm2, R = 100  a.u., tp = 20 fs. ω 0 = E01 – E00, i.e. one photon process is used.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Variation of transition probability with time in a two-electron QR. The various other parameters used are Es = 80  kV/cm, I = 8 × 1012  W/cm2, R = 100  a.u., tp = 50  fs: (a) square pulse, (b) sine square pulse, and (c) secant hyperbolic pulse.

These pulses are now available experimentally.^[54] The pulse rise and fall time are very sharp in the square pulse as compared to other two pulses. Hence, the system gets a sharp kick during the rise and fall of the pulse. Whereas, in the case of sine-square pulse, the pulse rise and fall are smooth, hence the interaction takes place slowly. In the case of secant-hyperbolic pulse of the same duration, the rise and fall time of pulse are between square and sine-square.

Figure  3 shows the dynamics as in the above cases but at lower laser intensity. The rest of the parameters are kept the same as those in Fig.  2. On comparing Figs.  2 and 3, it is evident that there is a drastic change in the transition probabilities when the intensity of laser is changed. For secant-hyperbolic pulse (Fig.  3(c)), the survival probability is 0.844 and the probability for transition from the ground state to the first excited state is 0.151. For a sine-square pulse (Fig.  3(b)) the transition probability reduces to 0.656 for the ground state and the transition from the ground state to the first excited state is 0.318. For square pulse (Fig.  3(a)) the transition from the ground state to the first excited state is maximum, being 0.558, and the ground state probability reduces to 0.227. When the laser intensity increases, the pumping of electrons to many higher levels takes place. So the number of states involved during the interaction increases.

To show the effect of pulse duration on the dynamics, we have shown the variation of transition probabilities with time in Fig.  4, for t_p = 50 fs. The other parameters are the same as those in Fig.  2. Since increasing the pulse duration gives the system more energy, the dynamics are modified. As in the case of Figs.  2 and 3, the probabilities change during the pulse, while these changes stabilize once the pulses are over. From Fig.  4, it is clear that the transition probability for the third excited state is maximum for all of the three types of pulses (square: 0.272, sine-square: 0.449, and secant-hyperbolic: 0.375).

The ends of the pulse results are shown in Figs.  5– 7. Figure  5 shows the variation of transition probability with the external static electric field. The transitions from the ground state to various excited states are shown in panels from (a)– (e) for the three different pulse shapes considered. The various other parameters used are E_s = 80  kV/cm, I = 8 × 10¹²  W/cm², t_p = 50 fs, and ω ₀ = E₀₁ – E₀₀. For the survival probability, the trend is opposite for the square and secant-hyperbolic pulse and constant for square pulse (Fig.  5(a)). For the transition from the ground state to the first excited state, the trend is the same for all of the three pulses. The variation of probabilities from the ground state to the second, third, and fourth excited states is shown in panels (c), (d), and (e) respectively.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Variation of transition probability with the external static electric field. The transitions from the ground state to various excited states are shown in panels (a)– (e) for the three different pulse shapes considered. The various other parameters used are Es = 80  kV/cm, I = 8 × 1012  W/cm2, R = 100  a.u., tp = 50 fs, and ω 0 = E01 – E00.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Variation of transition probability with the frequency of the laser beam. The transitions from the ground state to various excited states are shown in each panel for square pulse (a), sine-square pulse (b), and secant-hyperbolic pulse (c). The various other parameters used are Es = 80  kV/cm, I = 8 × 1011  W/cm2, R = 100  a.u., tp = 50 fs.

Fig.  7.

Figure Option ViewDownloadNew Window

Fig.  7. Variation of transition probability with the radius R of the QR. The transitions from ground state to various excited states are shown in panels from (a)– (f) for the three different pulse shapes considered. The various other parameters used are I = 8 × 1012  W/cm2, R = 100  a.u., tp = 50 fs, and ω 0 = E01 – E00. While in panels from (d)– (f), the external static electric field is 80  kV/cm, there is no electric field in panels (a)– (c).

In Fig.  6, we show the variation of transition probability with the frequency of the laser beam. The transitions from the ground state to various excited states are shown in each panel for the square pulse in panel  (a), sine-square pulse in panel  (b), and secant-hyperbolic pulse in panel  (c). The various other parameters used are E_s = 80  kV/cm, I = 8 × 10¹¹  W/cm², t_p = 50 fs. The large change in the probability is clearly shown from the figure for different pulse shapes.

Figure  7 shows the variation of transition probability with the radius of the QR. The transitions from the ground state to various excited states are shown in panels (a)– (f) for the three different pulse shapes considered. The various other parameters used are I = 8 × 10¹²  W/cm², t_p = 50 fs, and ω ₀ = E₀₁ – E₀₀. While in panels (d)– (f), the external static electric field is 80 kV/cm, there is no electric field in panels (a)– (c). As is evident from the figure, the change in the radius of the QR has an effect on the transition probability from the ground state to various excited states for all of the three types of pulse shapes. By comparing Figs.  7(b) and 7(e) and 7(c) and 7(f), we find that there is hardly any effect on the probabilities due to the change in the external static electric field for the sine-square and secant-hyperbolic pulse shapes, but there are changes in probability for the square pulse, as can be seen from Figs.  7(a) and 7(d).

In this study we have presented a detailed analysis of the dynamics of a two-electron QR system in short pulses. Such pulses with varying shapes are now available experimentally. It is shown that the shape of the pulse plays a crucial role in the excitation dynamics. The convergence parameter hardly plays any role in the dynamics. We have focused on the dynamics of the singlet states of the two-electron quantum ring system.