Corresponding author. E-mail: summit@bit.edu.cn
Project supported by the National Natural Science Foundation of China (Grant No. 11102019), the Aeronautical Science Foundation of China (Grant No. 2013ZC72006), and the Research Foundation of Beijing Institute of Technology, China.
In this paper, we consider the containment consensus control problem for multi-agent systems with measurement noises and time-varying communication delays under directed networks. By using stochastic analysis tools and algebraic graph theory, we prove that the followers can converge to the convex hull spanned by the leaders in the sense of mean square if the allowed upper bound of the time-varying delays satisfies a certain sufficient condition. Moreover, the time-varying delays are asymmetric for each follower agent, and the time-delay-dependent consensus condition is derived. Finally, numerical simulations are provided to illustrate the effectiveness of the obtained theoretical results.
Recently, the cooperative control of multi-agent systems has attracted much attention in physics, mathematics, complex systems, and control communities. The distributed coordination problems include several scenarios, such as formation control, [1] flocking, [2] consensus, [3] etc. In the last decade, the consensus of multi-agent systems has been rapidly developing in a new direction towards distributed cooperative control. Existing consensus research can be roughly divided into two kinds, namely: consensus without a leader[3– 5] and consensus with one or multiple leaders. For the single leader, the followers will converge to the state of leader, which is called the consensus tracking or leader-following consensus problem.[6– 8] However, in some circumstances, systems with multiple leaders have more superiorities. For example, a group of agents moves from one target to another but not all of the agents are equipped with sensors. The portion of the agents equipped with necessary sensors can be designated as leaders, and they have more ability to detect hazardous obstacles. The other agents who are without the necessary sensors are designated as followers. Then, the group can arrive at the destination safely given that the followers always stay within the safety area formed by the leaders. Thus, the containment control problem arises, where the followers converge to a convex hull that is spanned by the leaders.
In Ref. [9], the finite-time attitude containment control was considered for multiple rigid bodies under undirected topology. The authors in Ref. [10] gave some necessary and sufficient conditions to achieve containment control for first-order and second-order integrator agents with multiple stationary and dynamic leaders under directed networks. The containment control problems were investigated in Refs. [11] and [12] for a first-order and second-order integrator network under fixed and random switching directed communication topologies. The containment control problem for a collection of Euler– Lagrange systems was studied in Ref. [13]. The authors in Ref. [14] proposed a containment control protocol by exploiting the control input information of neighbors for first-order integrator network. The containment control of heterogeneous multi-agent systems was studied in Ref. [15]. The authors in Ref. [16] considered the containment control problem of second-order multi-agent systems with nonlinear dynamics. The distributed containment control problem for multi-agent systems with general linear dynamics was studied in Refs. [17]– [20]. In Ref. [21], the authors considered the adaptive containment control of general linear multi-agent systems with leaders of nonzero control input. The static containment control of linear uncertain multi-agent systems was studied in Ref. [22].
It should be noted that all of the aforementioned results about containment control have assumed that the communication channel is ideal. However, networks in the real world are often disturbed by noise because of an uncertain communication environment. In practical physical systems, delays exist ubiquitously due to actuation, control, communication, and computation. Thus, it is natural to consider noise and delays in the distributed protocols for cooperative control of multi-agent systems. The authors in Refs. [23] and [24] investigated the containment control of first-order integrator network under noisy measurements. The containment control problem for first-order and second-order multi-agent systems with time-varying delays was studied in Refs. [25] and [26].
However, measurement noise and time-varying delays always exist simultaneously in every physical system. To the best of our knowledge, there has been no report on the containment control of multi-agent systems, with both measurement noise and time-varying delays considered simultaneously. Motivated by the recent developments in containment control and stochastic approximation-type consensus protocols, in this paper we investigate the containment control of multi-agent systems with measurement noises and time-varying delays under the fixed directed topology.
The rest of this paper is organized as follows. In Section 2, we give several necessary definitions and lemmas. In Section 3, the containment control problem model is described. In Section 4, containment control with measurement noise and time-varying delays is investigated. In Section 5 we give some numerical simulations to illustrate the effectiveness of the proposed protocols. Finally, some conclusions are drawn in Section 6.
The following notations will be used throughout this paper: R denotes the set of real numbers, RN denotes the N-dimensional real vector space, RN× N denotes all of the real N × N matrices. For a given vector or matrix A, AT denotes its transpose, Tr(A) denotes its trace when A is square. For a given random variable X, E(X) denotes its mathematical expectation.
In this section, we introduce some basic concepts and results about graph theory and stochastic analysis.
A weighted digraph 𝒢 = (𝒱 , 𝓔 , 𝒜 ) consists of a finite vertex set 𝒱 = (𝒱 i, i = 1, 2, ..., N), an edge set 𝓔 ⊆ 𝒱 × 𝒱 , and a nonnegative adjacency matrix 𝒜 = (aij) ∈ RN× N. For an edge (𝒱 i 𝒱 j) ∈ 𝓔 , node 𝒱 i is called the parent node, node 𝒱 j the child node, and 𝒱 i is a neighbor of 𝒱 j. If (𝒱 i, 𝒱 j) ∈ 𝓔 , aij > 0 and aij = 0 otherwise. A graph with the property that (𝒱 i, 𝒱 j) ∈ 𝓔 implies (𝒱 j, 𝒱 i) ∈ 𝓔 for any vi, vi ∈ V is said to be undirected. The Laplacian matrix L = [lij] ∈ RN× N associated with 𝒜 is defined as 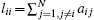
Assume Xt to be an Itō drift-diffusion process that satisfies the stochastic differential equation
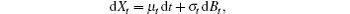
where Bt is a Wiener process. If f (t, x) is a twice-differentiable scalar function, then we can obtain the following Itō formula:

In higher dimensions, if 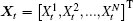

where ∇ Xf is the gradient of f with respect to Xt, HXf is the Hessian matrix of f with respect to Xt, and Tr is the trace operator.
One of the important properties about Itō stochastic integrals is Itō isometry
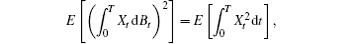
where E denotes the expectation with respect to the classical Wiener measure.
Consider a group of N agents, where the agents indexed by 1, 2, … , M are assigned as the followers and the agents indexed by M + 1, M + 2, … , N are denoted as leaders. We use F = {1, 2, ..., M} to denote the follower set and 𝓡 = {M + 1, M + 2, ..., N} to represent the leader set. The interaction graph among the N agents is represented by a directed graph 𝒢 lf, 𝒢 is the subgraph among M followers. In order to facilitate the description of the problem, we introduce a definition of the information exchange matrix.
Definition 1 (information exchange matrix) Let H = L + B, where H ∈ RM× M is the information exchange matrix. L = D – A ∈ RM× M is the Laplacian matrix associated with 𝒢 , D and A are an in-degree matrix and an adjacency matrix associated with the subgraph 𝒢 , respectively. B = diag(b1, b2, ..., bM), 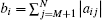
According to the fact that the leader has no neighbor, the Laplacian matrix 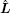
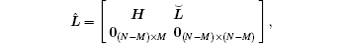
where H ∈ RM× M is the information exchange matrix, 
In this paper, the communication graph among the N agents satisfies Assumption 1.
Assumption 1 At least one leader has a directed path to each follower.
The next lemmas are needed in the following sections.
Lemma 1[9] Suppose that Assumption 1 holds, then each entry of 
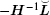
Lemma 2[27] Suppose that Assumption 1 holds. There exists a positive vector q = [q1, q2, ..., qN]T, such that q = H− 11N and PH + HTP > 0, where P = diag[1/q1, 1/q2 ..., 1/qN].
The dynamics of the i-th follower is described by
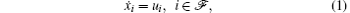
where xi ∈ R and ui ∈ R are the position and the control input of the i-th follower.
The dynamics of the j-th (M + 1 ≤ j ≤ N) leader is given as
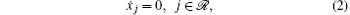
where xj ∈ R is the position of the j-th leader.
Remark 1 From expression (2) we can see that the leaders are stationary. In this situation, the leaders may be vertexes of a destination area. Generally, these leaders are used for pinning all of the agents to achieve containment.
Definition 2 (convex hull) A set K ⊂ Rn is said to be convex if (1 − α )x + α y ∈ K for any x, y ∈ K, and α ∈ [0, 1]. The convex hull of a finite set of points x1, x2, ..., xN ∈ Rn, denoted by Co{x1, x2, ..., xN}, which is defined as
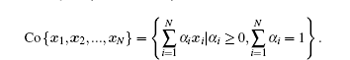
Let xf = [x1, x2, ..., xM]T represent the state of all of the followers and xl = [xM + 1, xM + 2, ..., xN]T represent the state of all of the leaders. That the containment without noise is achieved means that all of the followers can converge toward the convex hull spanned by the leaders. More specifically,
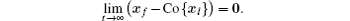
Due to the ubiquity of noise in physical systems, it is necessary to design a measurement-based distributed protocol ui such that the states of all followers can converge toward the convex hull spanned by the leaders asymptotically in noisy environments. Thus, one gives the definition of containment in the sense of mean square.
Definition 3 (mean square containment) That the mean square containment control is achieved means that
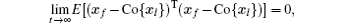
where E(X) denotes the mathematical expectation of random variable X.
In this section, we propose the following containment control algorithm, including the measurement noise and time-varying delays for Eq. (1):
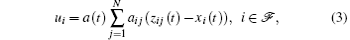
where zij(t) = xj(t − τ (t)) + σ ijwij denotes the measurement of the j-th agent state by the i-th agent at time t, with τ (t) being the time-varying communication delay satisfying 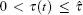
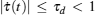
Assumption 2 The gain function a(t) satisfying 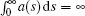
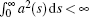
Remark 2 In fact, the gain function is used for reducing the measurement noises, and there are many functions meeting these properties, for example, a(t) = 1/(t + 1).
The dynamics of the closed-loop system from Eqs. (1)– (3) can be rewritten in a compact form:
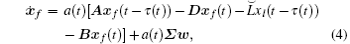
where the parameters 

aiσ i = [ai1σ i1, ai2σ i2, ..., aiNσ iN] ∈ R1× N, i = 1, 2, ..., M.
Define a new variable 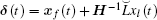

According to Lemma 1, one can obtain that δ (t) is a containment error. Thus, the closed-loop system (5) describes the dynamics of the containment error. The mean square containment control is achieved if
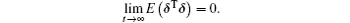
Then, one gives the following result.
Theorem 1 Suppose that Assumptions 1 and 2 hold, then the multi-agent system [Eqs. (1) and (2)] with protocol (3) will achieve the containment control in mean square if
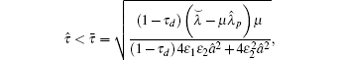
where ɛ 1, ɛ 2, 
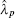

Proof Rewrite system (5) as a stochastic form

Take a Lyapunov function candidate as
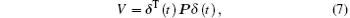
where P is a positive-definite diagonal matrix as defined in Lemma 2. By differentiating V, by Ito formula, one obtains
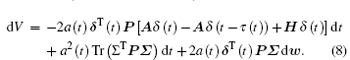
Since
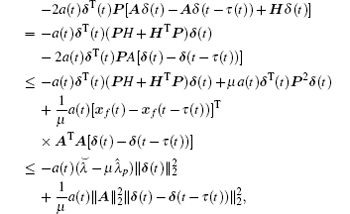
where 
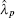
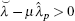

Therefore,

It is not difficult to obtain
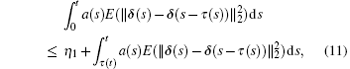
where
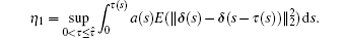
By Ito isometry and some mathematical operations, one can obtain
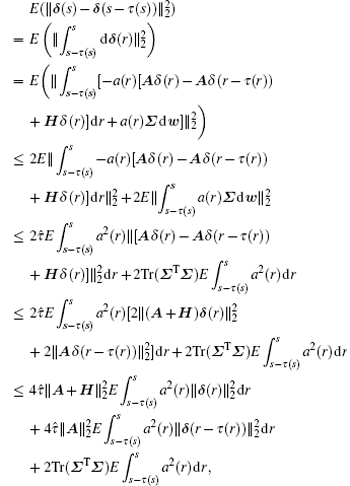
thus, for t ≥ τ (t)

where 
Moreover,
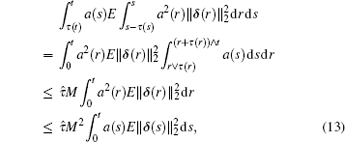
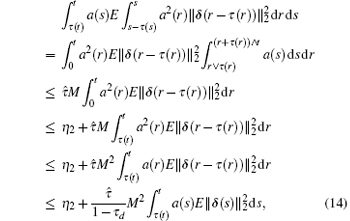
where
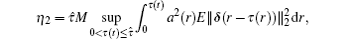
and
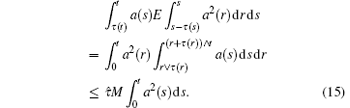
By substituting inequalities (12)– (15) into inequality (11), one obtains
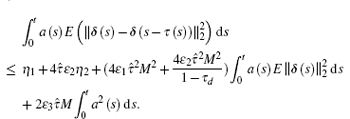
It then follows from inequality (10) that

where ɛ 4 = Tr(Σ TPΣ ), 

one obtains

By known results in Ref. [28], for any T > 0, there exists a constant CT, such that
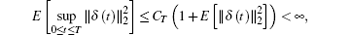
which implies that 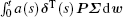

Therefore,
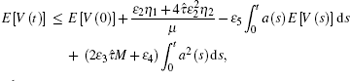
where

Then, by comparison principle, one can obtain
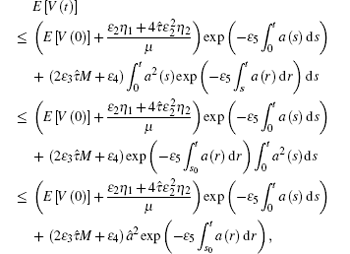
where s0 is a fixed constant located in the time interval [s, t]. This implies that 
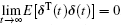
Remark 3 Note that the time-varying delays in expression (3) are asymmetric. Although self-delays on each agent for the control delays (the symmetric delays case) can be induced, for the communication delays in multi-agent systems it is necessary to consider asymmetric delays since each agent can receive its own information instantly. This is different from the work in Refs. [25] and [26].
Remark 4 For the case of asymmetric delays, one of the important conditions from Eqs. (4) and (5) is that the leader is static. If the leader is dynamic, then we cannot obtain Eq. (5) from Eq. (4). Thus, the analysis of asymmetric delays is more difficult than that of symmetric delays. In our future work, we may consider the containment consensus of multiple dynamic leaders with asymmetric delays and measurement noise.
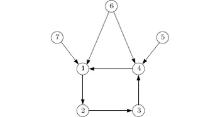
In this section, a simulation example is provided to validate the effectiveness of the containment. Consider a directed network containing four followers and three leaders. The topology is provided in Fig. 1.
Take the two-dimensional case for example. In simulation, we choose the initial position for each agent as (x1, y1)T = (6, 4)T, (x2, y2)T = (6, 1)T, (x3, y3)T = (12, 1)T, (x4, y4)T = (12, 4)T, (x5, y5)T = (18, 10)T, (x6, y6)T = (10, 18)T, and (x7, y7)T = (2, 10)T.
Take the stochastic disturbance intensity σ ij = 1, i, j = 1, 2, ..., 7. Let consensus-gain function be a(t) = 1/(1 + t). It is easy to see that a(t) is continuous, nonincreasing, and bounded by â = 1. It also satisfies Assumption 2.
Take the time-varying delay as τ 1(t) = 0.1(1 + sin (t))/2, thus, τ d = 0.05. From the topology in Fig. 1, one can obtain that 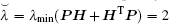
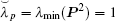

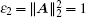
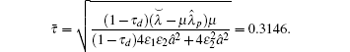
Clearly, the inequality condition 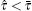
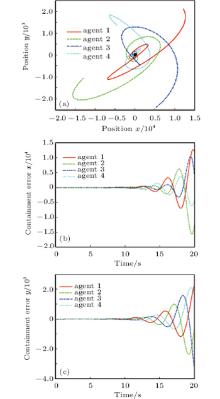
 | Fig. 2. (a) States of different agents, and variations of containment errors of positions (b) x and (c) with τ 1(t) for different agents. |
From Figs. 2(a)– 2(c), we can see that the positions of the follower agents converge to the convex hull spanned by leaders in the sense of mean square.
Take the time-varying delay as τ 2(t) = (1 + sin(t))/2, thus, τ d = 0.5. From the topology in Fig. 1, one can obtain 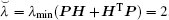
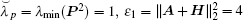
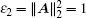
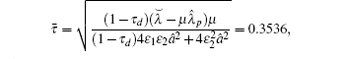
the inequality condition 
In this paper, we investigate the containment control problem for multi-agent systems with measurement noises and time-varying communication delays. The measurement noises and asymmetric time-varying delays are considered simultaneously in the construction of the containment control algorithm. A delay-dependent sufficient condition for containment consensus in the sense of mean square is derived. Our future work will include the containment control problem for multi-agent systems with multiple dynamic leaders or under switching topologies.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|