Cite this Article
Zhang Zhi-Yong, Chen Yu-Fu. Conservation laws of the generalized short pulse equation* . Chinese Physics B, 2014, 24(2): 020201  
Permissions
Conservation laws of the generalized short pulse equation*
Zhang Zhi-Yonga)†, Chen Yu-Fub)
College of Sciences, North China University of Technology, Beijing 100144, China
School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author. E-mail: zhiyong-2008@163.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 11301012 and 11271363), the Excellent Young Teachers Program of North China University of Technology (Grant No. 14058) and the Doctoral Fund of North China University of Technology (Grant No. 41).

Abstract

We show that the generalized short pulse equation is nonlinearly self-adjoint with differential substitution. Moreover, any adjoint symmetry is a differential substitution of nonlinear self-adjointness, and vice versa. Consequently, the general conservation law formula is constructed and new conservation laws for some special cases are found.

Keyword: 02.20.Sv; 02.30.Jr; 11.30.–j; nonlinear self-adjointness with differential substitution; adjoint symmetry; conservation law
1. Introduction

The short pulse equation

was first introduced by Schä fer and Wayne as a model equation to describe the propagation of ultra-short light pulses in silica optical fibres.[1] Later, the properties of Eq.  (1), such as integrability, bi-Hamiltonian structure, and its exact solutions, have been extensively studied. (See Refs.  [2]– [4] and the references therein.)

This paper is concerned with the conservation laws of the generalized short pulse equation

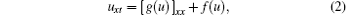
from the point of view of nonlinear self-adjointness with differential substitution, where f = f(u) and g = g(u) are two nonconstant analytic functions of u. Obviously, equation  (1) is a particular case of Eq.  (2) with g(u) = u3/6 and f(u) = u. Complete Lie symmetry classification and reductions of Eq.  (2) have been performed in Ref.  [5].

The conservation law has an important characteristic of studying partial differential equations (PDEs), such as integrability and linearization, constants of motion, analysis of solutions, and numerical solution methods.[6– 13] Thus many researchers have developed new and effective methods to construct conservation laws of PDEs.[13– 17] The method that we have adopted here is the nonlinear self-adjointness with differential substitution.[16, 17] Approximate nonlinear self-adjointness and approximate conservation laws were studied in Refs.  [17]– [19].

We will now briefly review the main idea of nonlinear self-adjointness with differential substitution. Consider a system of m PDEs with r-th order

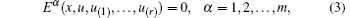
where x = (x1, … , xn) is an independent variable set and u = (u1, … , um) is a dependent variable set, u(i) denotes all i-th x derivatives of u. Note that the summation convention for repeated indices will be used unless otherwise stated.

Let 𝓛 be the formal Lagrangian of system  (3), which is written as

where vβ are the introduced new dependent variables, and then the adjoint equations of system  (3) will be defined by

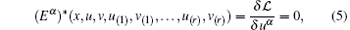
where δ /δ uα is the Euler operator written as

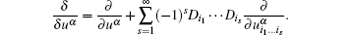
The definition of nonlinear self-adjointness with differential substitution is then given as follows.[16, 17]

Definition 1 The system (3) is said to be nonlinearly self-adjoint with differential substitution if the adjoint system  (5) is satisfied for all solutions of system  (3) upon a differential substitution v = φ (x, u, u(1), … , u(s)) such that v ≠ 0.

Definition 1 means that the adjoint system  (5), after having been inserted by the differential substitution v = φ (x, u, u(1), … , u(s)), holds identically in the solution space of the original system  (3), thus Definition  1 is equivalent to the following equality:

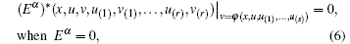
which is called the determining system of differential substitution.

Since the key point of studying nonlinear self-adjointness with differential substitution is to search for the differential substitution, in the next section we will show that the adjoint symmetries admitted by Eq.  (2) are the required differential substitutions, and then give the general conservation law formula.

2. Nonlinear self-adjointness with differential substitution

Following the idea of nonlinear self-adjointness with differential substitution, we first introduce the formal Lagrangian of Eq.  (2) in the symmetric form of mixed derivatives

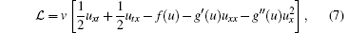
where v is a new introduced dependent variable, and then the adjoint equation of Eq.  (2) is

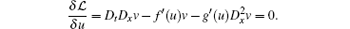
Assume the differential substitution v = ψ (x, t, u, ux, ut, … ), which does not contain uxt nor its differential results since they can be expressed through Eq.  (2), then by the differential substitution determining equations  (6), we will obtain

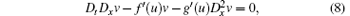
when equation  (2) holds.

On the other hand, by means of the infinitesimal symmetry criterion for PDEs, [16] the determining equation of a generalized symmetry X = φ (x, t, u, ux, ut, … )∂ u is

where

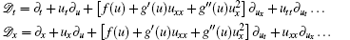
are total derivative operators which express uxt and their derivatives through Eq.  (2). The adjoint equation of Eq.  (9) is

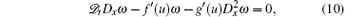
which is the determining equation of an adjoint symmetry X = ω (x, t, u, ux, ut, … , )∂ u. Obviously, solutions of Eq.  (10) are not solutions of Eq.  (9), thus in general an adjoint symmetry is not a symmetry of Eq.  (2).

Obviously, in the solution space of Eq.  (2), the determining equation of differential substitution (8) is identical to the adjoint symmetry determining equation (10), thus we have the following theorem:

Theorem 1 Any adjoint symmetry of Eq.  (2) is a differential substitution of nonlinear self-adjointness, and vice versa.

Thus, in order to find the differential substitutions of nonlinear self-adjointness, we will perform adjoint symmetry classification of Eq.  (2).

2.1. Classification of adjoint symmetry

To simplify our calculations, we use the following equivalence transformation for Eq.  (2). In particular, by simple calculations, we have the following proposition:

Proposition 1 Any transformation of the form

where c1c3c5 ≠ 0, is an equivalence transformation of Eq.  (2), i.e., transformation (11) maps Eq.  (2) into

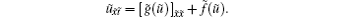
In what follows, we consider the adjoint symmetry of Eq.  (2) in the form of

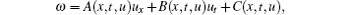
and then, by substituting it into Eq.  (10) and separating with respect to x-, t-derivatives of u, we obtain B = α (t), A = – α (t)g′ (u)+ β (x, t), and C = γ (t)u+ μ (x, t), where α , β , γ , and μ satisfy

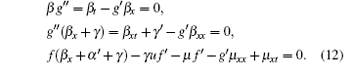
For arbitrary functions f(u) and g(u), the differential substitution is ω = ut – g′ (u)ux. For special f(u) and g(u), the differential substitutions of nonlinear self-adjointness are extended. Note that ci (i = 1, … , 6) are arbitrary constants such that the differential substitution ω ≠ 0.

2.1.1. g(u) = u

In this case, equation  (2) becomes

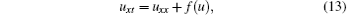
which is obtained from the variational principle with the Lagrangian 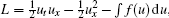, thus the adjoint symmetry and symmetry are identical.

Then, after routine computations, for arbitrary f(u), the symmetry is

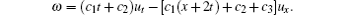
In particular, for f(u) = up(p ≠ 1), the symmetry is then

2.1.2. g(u) ≠ u

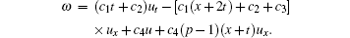
In this case, one has β = γ = 0. If f(u) = u, there is no additional new differential substitution to be found. Thus for f(u) ≠ u, equation  (12) becomes

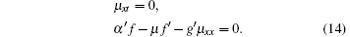
From the first equation in Eq.  (14), we obtain μ = m(x)+ n(t), where m(x) and n(t) are two arbitrary functions. The second equation then becomes

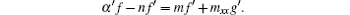
Since the left side in the above equation is a function of t and u while the right side is a function about x and u, we thus have f = f′ = g′ , which means f = g = eu, and

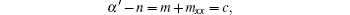
which gives n = α ′ – c, m = c1 sin x+ c2 cos x+ c, thus the adjoint symmetry is

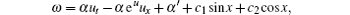
where α = α (t) is an arbitrary function.

2.2. Conservation law

We will use the following theorem to construct conservation laws.[20]

Theorem 2 Any infinitesimal symmetry (local and nonlocal)

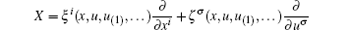
of system  (3) leads to a conservation law Di(Ci) = 0 that is constructed by the formula

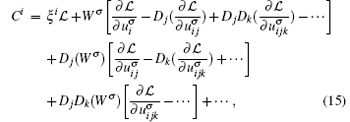
where 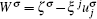and 𝓛 is the formal Lagrangian, which is written in the symmetric form in the mixed derivatives.

By Theorem 2, after substituting formal Lagrangian  (7) into Eq.  (15) and then performing proper arrangements, we obtain the following conservation law formula of Eq.  (2).

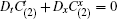
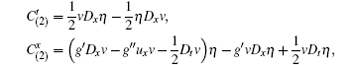
Theorem 3 A conservation law of Eq.  (2) is given by

where the differential substitution v = ψ determined by Eq.  (8) and X = η (x, t, u, ux, ut, … )∂ u is a generalized symmetry of Eq.  (2).

In what follows, we consider three special examples to illustrate the effectiveness of nonlinear self-adjointness with differential substitution in the construction of conservation laws. Note that for the following examples X = η (x, t, u, ux, ut, … )∂ u is a generalized symmetry of the corresponding PDEs.

Example 1 The first example is to consider Eq.  (2). For arbitrary functions f(u) and g(u), the differential substitution is v = ut – g′ ux, thus by Theorem  3 and considering Dxv = uxt – (g′ ux)x = f, we have

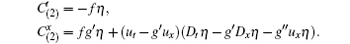
When g(u) = u3/6, f(u) = u, equation  (2) becomes the short pulse equation  (1), which is admitted by the infinitesimal operators X1 = ux∂ u, X2 = ut∂ u, and X3 = (u – xux+ tut)∂ u. Then by using η = u – xux+ tut and after proper arrangements, we obtain

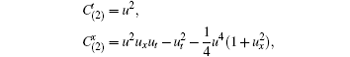
which is identical to the results in Ref.  [17].

Example 2 The second example to be considered is

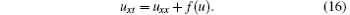
For arbitrary function f(u), the new added differential substitutions are v1 = ux and v2 = tut – xux – 2tux. Then for the differential substitution v2+ q1v1 with an arbitrary constant q1, the conservation laws 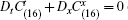of Eq.  (16) are given by

In particular, for f(u) = up(p ≠ 1), the extended differential substitution is v3 = u+ (p – 1)(x+ t)ux, we then have

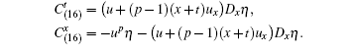
Example 3 The last example is

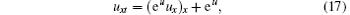
whose conservation laws 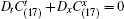of Eq.  (17) are

where the differential substitutions v = α ut – α euux+ α ′ + c1 sin x+ c2 cos x with an arbitrary function α = α (t).

3. Conclusion

We show that the generalized short pulse equation is nonlinearly self-adjoint with differential substitution and its adjoint symmetries are the required differential substitutions. The general conservation law formula is then presented and new conservation laws are constructed.

Reference
1 Schäfer T and Wayne C E 2004 Physica D 196 90 [Cited within:1] [JCR: 1.669]
2 Brunelli J C 2006 Phys. Lett. A 353 475 DOI:10.1016/j.physleta.2006.01.009 [Cited within:1] [JCR: 1.11]
3 Fu Z T, Chen Z, Zhang L N, Mao J Y and Liu S K 2010 Appl. Math. Comput. 215 3899 DOI:10.1016/j.amc.2009.11.038 [Cited within:1] [JCR: 0.75]
4 Sakovich A and Sakovich S 2005 J. Phys. Soc. Jpn. 74 239 DOI:10.1143/JPSJ.74.239 [Cited within:1] [JCR: 2.087]
5 Liu H, Li J and Liu L 2012 Stud. Appl. Math. 129 103 DOI:10.1111/sapm.2012.129.issue-1 [Cited within:1] [JCR: 1.313]
6 Olver P J 1993 Applications of Lie Groups to Differential Equations New York Springer-Verlag [Cited within:1]
7 Wang X, Chen Y and Dong Z Z 2014 Chin. Phys. B 23 010201 DOI:10.1088/1674-1056/23/1/010201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
8 Lou S Y, Hu X R and Chen Y 2012 J. Phys. A: Math. Theor. 45 155209 DOI:10.1088/1751-8113/45/15/155209 [Cited within:1] [JCR: 1.766]
9 Song J F, Qu C Z and Qiao Z J 2011 J. Math. Phys. 52 013503 DOI:10.1063/1.3530865 [Cited within:1] [JCR: 1.296]
10 Su J R, Zhang S L and Li J N 2010 Commun. Theor. Phys. 53 37 DOI:10.1088/0253-6102/53/1/08 [Cited within:1]
11 Zhao G L, Chen L Q, Fu J L and Hong F Y 2013 Chin. Phys. B 22 030201 DOI:10.1088/1674-1056/22/3/030201 [Cited within:1] [JCR: 1.148] [CJCR: 1.2429]
12 Sun X T, Han Y L, Wang X X, Zhang M L and Jia L Q 2012 Acta Phys. Sin. 61 200204(in Chinese) [Cited within:1] [JCR: 1.016] [CJCR: 1.691]
13 Bluman G W, Cheviakov A F and Anco S C 2010 Applications of Symmetry Methods to Partial Differential Equations New York Springer-Verlag [Cited within:2]
14 Kara A H and Mahomed F M 2006 Nonlinear Dyn. 45 367 [Cited within:1]
15 Naz R, Mahomed F M and Mason D P 2008 Appl. Math. Comput. 205 212 DOI:10.1016/j.amc.2008.06.042 [Cited within:1] [JCR: 0.75]
16 Gand arias M L 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3523 DOI:10.1016/j.cnsns.2014.02.013 [Cited within:3] [JCR: 2.773]
17 Ibragimov N H 2011 Archives of ALGA 7/8 1 [Cited within:5]
18 Zhang Z Y 2013 J. Phys. A: Math. Theor. 46 155203 DOI:10.1088/1751-8113/46/15/155203 [Cited within:1] [JCR: 1.766]
19 Zhang Z Y and Chen Y F 2014 IMA J. Appl. Math. first published online May 8, 2014 DOI:10.1093/imamat/hxu017 [Cited within:1]
20 Ibragimov N H 2007 J. Math. Anal. Appl. 333 311 DOI:10.1016/j.jmaa.2006.10.078 [Cited within:1] [JCR: 1.05]