Corresponding author. E-mail: hli@fjnu.edu.cn
Project supported by the National Natural Science Foundation of China (Grant No. 61178089), the Key Program of Science and Technology of Fujian Province, China (Grant No. 2011Y0019), and the Educational Department of Fujian Province, China (Grant No. JA13074).
An analytic equation interpreting the intensity of ultrasound-modulated scattering light is derived, based on diffusion theory and previous explanations of the intensity modulation mechanism. Furthermore, an experiment of ultrasonic modulation of incoherent light in a scattering medium is developed. This analytical model agrees well with experimental results, which confirms the validity of the proposed intensity modulation mechanism. The model supplements the existing research on the ultrasonic modulation mechanism of scattering light.
Ultrasound-modulated optical tomography (UOT), [1– 3] also known as acousto-optical tomography (AOT), is an acousto-optic interaction imaging modality. With high spatial resolution of ultrasonic location and high sensitivity of optical detection, UOT is a promising noninvasive biological tissue imaging technology. With the improvement of experimental apparatuses and technical routes over the last 30 years, the imaging depth of UOT has reached 3– 5 cm, [4, 5] with its spatial resolution determined by ultrasound (up to the maximum of dozens of micrometers)[6] and its contrast ratio provided by optics. In contrast with photoacoustic imaging technology (PAT), [7, 8] it can provide not only the optical absorption coefficient[9] but also the scattering coefficient[10] of tissue, and thus it is able to gain much imaging information of tissue. However, its theoretical foundation, or what is known as the “ acousto-optic interaction mechanism” in the scattering medium, still remains a mystery. The previous ultrasonic modulation model cannot explain all experimental phenomena. Therefore, further exploration of its mechanism is still needed.
Biological tissue is a multiple random scattering medium. The acousto-optic interaction mechanism in tissues is not only a fundamental problem of UOT that has to be solved, but it is also a principal problem vital to the final image processing and reconstruction. Currently, there are three possible mechanisms. (i) The optical properties of the scattering medium (including absorption coefficient, scattering coefficient, and refractive index) change after being sensed by the mechanical wave in the ultrasonic field, resulting in the modulation of scattering light. This mechanism is an intensity modulation mechanism.[11– 13] Both coherent and incoherent light can be used for this mechanism. However, this mechanism has not been reported by experiments yet. (ii) Due to the forced vibration of scatters in the scattering medium with an ultrasonic field, the optical distance and phase of coherent scattering light change correspondingly, which is finally manifested by the intensity variation of coherent light speckles with the ultrasonic wave. This mechanism has been studied by using dynamic light scattering (DLS).[14] (iii) The refractive index variation of a medium caused by the ultrasonic field also influences the optical distance change of scattering light, which is manifested by modulation of the scattering light. The latter two mechanisms are phase modulation mechanisms, requiring a light source with good coherence.[15] These two mechanisms were verified by using Monte Carlo simulation.[16] The interaction mechanism between scattering light and impulse ultrasonic field[17, 18] in the scattering medium with anisotropy[19] and uneven space[20, 21] were given successively.
Based on an intensity modulation mechanism, an analytic equation interpreting the intensity of scattering light subjected to ultrasonic modulation is derived in this paper based on the diffusion theory. Furthermore, ultrasonic modulation of incoherent light in the scattering medium is developed, which supplements the existing research on the ultrasonic modulation mechanisms of scattering light.
Considering the strong light scattering of tissues, an understanding of light traveling in biological tissue does not need to involve the interaction among optical fields and a diffraction effect, but attention has to be paid to the transmission of light intensity (light power) in the tissue.
The time-dependent transmission equation without a light source can be obtained under approximate diffusion[22]
 |
where Δ is the Laplace operator, φ (r, t), v, μ a, and μ s are the light energy flow rate, the light velocity, the absorption coefficient, and the scattering coefficient, and D = 1/3[μ a+(1− g)μ s] is the diffusion coefficient.
Generally, biological tissues always scatter light more than absorb it, that is, satisfying 3Dμ a ≪ 1. Under the non-ultrashort pulsed lights, the distribution of the light energy flow rate can be regarded simply as a postponed time variable. Therefore, equation (1) can be simplified into
 |
Ultrasonic waves are a kind of mechanical stressed elastic longitudinal wave. When an ultrasonic wave travels in a continuous elastic medium, elastic strain or stress is produced in the medium as time and space vary, thus changing the medium density. If the ultrasonic wave travels as a plane wave forward along the y axis, the medium density can be expressed as[23]
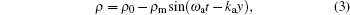 |
where ρ 0 and ρ m are the static medium density and the amplitude of density variation, ω a and ka are the angular frequency and the wave vector of ultrasound. The relationship between ρ m and pm (amplitude of acoustic pressure) is[23]
 |
where u is the sound velocity.
The variation of medium density will surely change the densities of absorption and scattering grains in the medium in the same law. Take the simplest one-dimensional space for example. Such a one-dimensional space is equal to the modulated light intensity detected on the z axis (optical axis) when a wide beam of continuous light is vertically irradiated on a semi-infinite scattering medium. Since the common focused ultrasound has a focal length of about 2 cm and very small width (submillimeter or millimeter), the optical parameters of a medium on the z axis can be approximately considered as only changing with time under the effect of an ultrasonic field. Therefore, the absorption coefficient and scattering coefficient of the medium in the focal area can be expressed as
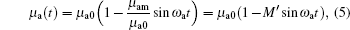 |
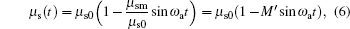 |
where μ a0 and μ s0 are the initial absorption and scattering coefficient of the medium, μ am and μ sm are the variation of absorption and the scattering coefficient of the medium, and
 |
It can be known from Eq. (7) that M′ is determined by the acoustic property of the medium, which is proportional to the amplitude of acoustic pressure but inversely proportional to the square of sound velocity. Suppose u = 1500 m/s (u is the travel speed of ultrasound in biological tissues), pm = 2× 105 Pa, and ρ 0 ∼ 1000 kg/m3, then it can be estimated that M′ ∼ 10− 4. This demonstrates the little change of the absorption coefficient and the scattering coefficient of the medium caused by the ultrasonic field in biological tissues.
When the incident light source is a wide beam of continuous light, the light traveling in the tissue with an ultrasonic field satisfies the diffusion equation
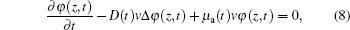 |
where
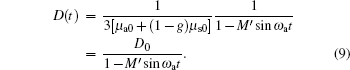 |
Solve Eq. (8) by using the separation of variables. Substitute φ (t, z) = Z(z)T(t) into Eq. (8), and set
 |
where λ is a constant.
Then, equation (10) can be separated into Eqs. (11) and (12)
 |
 |
Compose the eigenvalue problem from boundary conditions Z(z)| z→ ∞ = 0 and Z(z)| z=0 = Z0, then
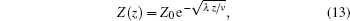 |
where the eigenvalue λ > 0.
Compare Eq. (13) with the most common and simplest steady diffusion solution [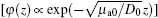
 |
Substitute Eq. (14) into Eq. (11), then we obtain
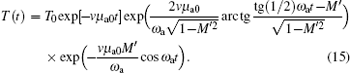 |
Considering the practical estimate M′ ∼ 10− 4, equation (15) can be approximately expressed as
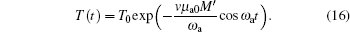 |
Combining Eqs. (13), (14), and (16), the analytical solution of Eq. (8) can be given by
 |
where the initial energy flow rate is φ 0 = T0Z0.
Given a fixed light source size and observation direction, there is a linear relationship between the light intensity and the energy flow rate in the same place of the medium. Hence, the scattering light intensity in the medium modulated by an ultrasonic field is
 |
where I0 is the initial light intensity, and M′ ∝ Pm/u2.
Equation (18) is applicable to both coherent and incoherent sources. Supposing that μ ao = 100m− 1, v ∼ 3× 108 m/s, and M′ ∼ 10− 4, equation (18) can be approximately expressed as
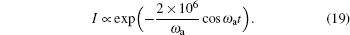 |
In accord with Eq. (19), figure 1(a) shows the rule of the scattering light intensity with time when the ultrasonic frequency is 1 MHz or 2 MHz. Figure 1(b) shows the modulation depth of modulated light intensity versus the frequency of ultrasound. The modulation depth is defined as the peak-to-peak value divided by the average value of the ultrasound-modulated light intensity.
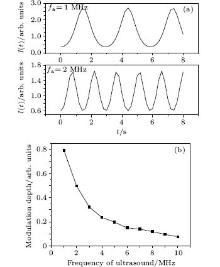 | Fig. 1. (a) Rule of the scattering light intensity with time. (b) Modulation depth of modulated light intensity versus the frequency of ultrasound. |
As shown in Eq. (18) and Fig. 1, the diffuse light intensity decays forward along the z axis. Under the effect of an ultrasonic field, the scattering light intensity presents a periodic variation as the ultrasonic frequency changes, and its modulation frequency is the same as the ultrasonic frequency (Fig. 1(a)). This is in good accordance with general experimental findings.[14, 24] The modulation depth of modulated light intensity, known as modulation efficiency, is determined by the acoustic properties and optical properties of the medium, and it increases with the increase of the amplitude of acoustic pressure (pm) and the optical absorption coefficient of medium (μ a0), but it declines with increasing acoustic angular frequency (Fig. 1(b)). In another paper, [25] we compared the imaging sensitivity and signal-to-noise with 1, 2.25, 5, and 10 MHz center frequency of impulse ultrasound in UOT. Experimental results validate Eq. (18), namely, a higher modulation efficiency of scattering light can be gained by the use of lower ultrasound frequencies and increasing ultrasonic energy. The conclusion that modulation efficiency is closely correlated with the absorption coefficient, but not with the scattering coefficient, is right, assuming a wide beam of continuous light vertically irradiated on a semi-infinite medium.
The experimental setup is shown in Fig. 2. The white light source (HL-2000-HP, output power: 20 W) shines on the sample after being expanded into a beam of 3-cm-diameter parallel light through the beam expander. The sample is the 1-cm-thick intralipid solutions (scattering coefficient: 5.6 cm− 1. Along the vertical optical axis, the ultrasonic pulser-receiver (Panametrics 5800PR) drives the ultrasonic transducer (Panametrics A314S; center frequency: 1 MHz; pulse width: 0.48 MHz; diameter: 0.75 inches; focal length: 1.006 inches) to generate pulsed ultrasound (repetition frequency: 2 K; pulse energy: 100 μ J) on the sample. The ultrasound travel direction (y axis) is perpendicular to the optical axis (z axis). The ultrasonic focal area falls on the optical axis due to its largest intensity, thus having the incident light passing through the ultrasonic focal area to gain larger optical signals modulated by the ultrasonic wave. Two tiny holes, with a fixed diameter of 1 mm, are put between the sample and the photomultiplier (PMT). One of these holes is put in front of the detecting window of the PMT to control the practical detection area of the PMT. The other one is put about 13.5 cm away from the sample and 10.5 cm away from the PMT. These two holes both enable the PMT to more easily detect ultrasonic modulation signals and improve the signal-to-noise ratio of the UOT efficiently.[26] The finally detected ultrasound-modulated white light signals are displayed on the oscilloscope after being amplified through the amplifier. The average value and the peak-to-peak value of the ultrasound-modulated light signal displayed on the oscilloscope are defined as the intensity of transmitted beam (Idc) and modulated light intensity (Iac), respectively. The quotient of half the Iac divided by the Idc is the modulation depth (M).
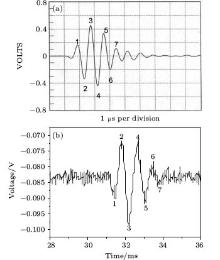
A pulsed ultrasonic wave with a 1 MHz center frequency and ultrasound-modulated white light are shown in Figs. 3(a) and 3(b), respectively. As shown in Fig. 3, an ultrasound-modulated white light signal is very similar to a pulsed ultrasonic wave, both in upside-down state. This is because it is the upside-down image of ultrasonic grating in the medium formed through the tiny hole that the PMT detected. Figure 4(b) originated from the fast Fourier transform (FFT) of the ultrasound-modulated white light signal, which indicates that the frequency spectral intensity of the detected optical signals concentrate at the zero frequency when the ultrasound is off, whereas the spectral intensity of other frequencies goes almost to zero. Therefore, the zero frequency intensity represents the unmodulated light signal. When the ultrasound is on, except for the great spectral intensity at zero frequency, the detected modulated light also has a significantly greater spectral intensity within the 0.5– 1.5 MHz frequency range than that under no ultrasonic effect, which is in good accordance with the spectral range of pulsed ultrasound (Fig. 4(a)). This demonstrates that the intensity of scattering light passing through the ultrasonic field changes periodically with the ultrasonic frequency, and the modulation frequency is the same as the ultrasonic frequency. This experimental result further confirms Eq. (18). Figure 5 represents the ultrasound-modulated laser light and the ultrasound-modulated white light shown in an oscilloscope. The wavelength of the laser is 632.8 nm. Obviously, given the similar intensity of the transmitted beams (average value of modulating signal) and the same ultrasonic intensity, the peak-to-peak value of ultrasound-modulated laser signals is 96.54 mV, significantly higher than that of ultrasound-modulated white light signals (23.01 mV). This indicates that a coherent source is more applicable as the light source of UOT because its ultrasonic modulation is far more efficient than that of an incoherent source.
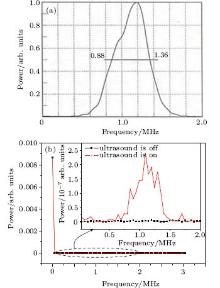 | Fig. 4. (a) Frequency spectrum of ultrasound. (b) Frequency spectrum of ultrasound-modulated white light. |
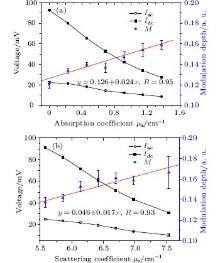
Considering the great impact of PMT’ s detection location on the modulation depth, [26] the author moved the PMT along the y axis slowly away from the optical axis until acquiring the largest modulating signal (Iac). The PMT was then kept at the same detection location to study the relationship between the ultrasound-modulated white light intensity and the absorption coefficient and scattering coefficient of the medium. The experimental results (Fig. 6) demonstrate that the peak-to-peak value (Iac) and average value (Idc) of the modulating signal decrease with an increase of the absorption coefficient and scattering coefficient of the medium. A linear increase of the modulation depth is observed with the increase of the absorption coefficient and scattering coefficient of the medium. The modulation depth increases by 0.024 for every 1 cm− 1 increase of the absorption coefficient and 0.017 for every 1 cm− 1 increase of the scattering coefficient. Compared with the coherent source, [24] the modulation depth of an incoherent source is less sensitive to the absorption coefficient and the scattering coefficient of the medium.
Considering the high scattering characteristic of light in biological tissues, this paper derives an analytical equation interpreting the intensity of ultrasound-modulated scattering light, based on the diffusion theory. This analytical equation is a time-space function. When a wide beam of continuous light is vertically irradiated on a semi-infinite scattering medium, the intensity of diffused light not only decays with its travel distance (z) in the medium but also changes periodically as the ultrasonic frequency changes. The modulation efficiency of scattering light is determined by the acoustic properties and optical properties of the medium, which is proportional to the amplitude of acoustic pressure (pm) and the optical absorption coefficient of the medium (μ a0), but it is inversely proportional to the square of sound velocity and acoustic angular frequency. Finally, the ultrasonic modulation of incoherent light in the scattering medium is developed through the experiment, which confirms the validity of the intensity modulation mechanism of the acoustic-optic interaction in the scattering medium and supplements existing research on the ultrasonic modulation mechanism of scattering light. Compared with a coherent source, an incoherent source has lower efficient ultrasonic modulation and its modulation depth is less sensitive to the absorption coefficient and scattering coefficient of the medium. Therefore, an incoherent source is not the ideal light source for UOT.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|