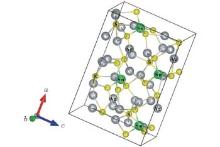
According to the literature, Ag₈SnS₆ belongs to Pna21 space group of the orthorhombic crystal system.^[10] It contains four formula units in a single unit cell. There are two different types of S atoms in the Ag₈SnS₆ crystal structure. The first type connects Sn and Ag atoms together, and the other only form a bond with Ag atoms. The crystal structure of Ag₈SnS₆ is presented in Fig. 1. The equilibrium structural parameters were determined by using the Birch– Murnaghan equation.^{[22, 23]} The Ag₈SnS₆ structure was optimized with the given parameters in Section 2. Experimental data are compared with geometry optimization results (see Table 1). Experimental^[10] and calculated values of the lattice parameters match with each other very well. The optimized structure was used to calculate electronic and optical properties in the next section.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Structure of Ag8SnS6.

Table 1.

Table 1.

Table 1. Experimental and calculated crystal structure parameters of Ag8SnS6.   a/Å b/Å c/Å V/Å 3 Experimental data 15.2980 7.5480 10.6990 1235.41 Calculation results 15.4883 7.65393 10.8697 1288.56

Table 1. Experimental and calculated crystal structure parameters of Ag8SnS6.

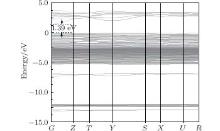
The band structure of Ag₈SnS₆ is shown in Fig. 2. Ag₈SnS₆ is a direct band gap semiconductor, and the conduction band minimum and the valence band maximum are at the G point. The band gap is about 0.58 eV, which is obviously less than the experimental value of 1.39 eV. The underestimated energy band gap values often come forth in the calculated simulation. This is related to the DFT limitations, and it does not take into account the discontinuity in the exchange– correlation potential.^[24] For the sake of resolving this incongruity, the scissors operator is introduced.^{[15, 25]} It can eliminate the difference between the experimental and calculated data, and shift the unoccupied conduction band with respect to the valence band. The scissors operator at 0.81 eV was performed in the present work. Table 2 shows band gap energies along with the valence to conduction band transition of Ag₈SnS₆. As we know, when the irradiation photon energy is greater than the semiconductor band gap, the electron will be excited to create an electron– hole pair. Photons exhibit a wavelike character with the wavelength (λ ), which is related to the photon energy E_λ by

where h is Plank’ s constant, and c is the speed of light.^[26] Therefore, in order to use visible light, the E_g of semiconductors should be below 3.0 eV (above 400 nm).^[27] The narrower the energy band gap, the excited electrons and holes separate and migrate more easily. Because Ag₈SnS₆ has the narrow band gap of 1.39 eV, the electrons in the valence band of Ag₈SnS₆ are easily excited to the conduction band under visible light radiation. Consequently, Ag₈SnS₆ has excellent photocatalytic capability in the visible light area.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Calculated band structure of Ag8SnS6.

Table 2.

Table 2.

Table 2. Symmetry of the valence to conduction band transition of Ag8SnS6. VB: valence band; CB: conduction band.     CB     G Z T Y S X U R VB G 1.39 1.51 1.54 1.42 1.49 1.45 1.52 1.48 Z 2.35 2.48 2.50 2.39 2.45 2.41 2.48 2.45 T 2.59 2.72 2.75 2.63 2.70 2.66 2.73 2.69 Y 2.01 2.14 2.17 2.05 2.12 2.08 2.14 2.11 S 2.82 2.95 2.98 2.86 2.93 2.89 2.95 2.92 X 2.73 2.86 2.89 2.77 2.84 2.80 2.87 2.83 U 2.72 2.85 2.88 2.76 2.83 2.78 2.85 2.82 R 2.84 2.97 3.00 2.88 2.95 2.91 2.97 2.94

Table 2. Symmetry of the valence to conduction band transition of Ag8SnS6. VB: valence band; CB: conduction band.

The partial and total density of states (PDOS and TDOS) can be used to analyze the composition of the energy bands. The DOS of Ag₈SnS₆ is presented in Fig. 3. The conduction band between 1.40 eV and 3.80 eV is contributed from Ag 5s and 5p states, Sn 5s and S 3p states, and these states are hybridized. The valence band is split into four sub-bands. In the uppermost valence band, Ag 4d, S 3p, and a small quantity of Sn 5p states are observed between 0 and – 5.40 eV. The second sub-band is contributed from Sn 5s and S 3p states, which is from – 6.80 eV to – 7.30 eV. The third one locates at 12.00– 12.40 eV, which consists of Ag 4d, Ag 5s, Ag 5p, Sn 5p, S 3s, and S 3p states. The lowest one is from – 12.70 eV to 13.00 eV. It is the main contribution of S 3s state, Sn 5s states, and Ag 4d, 5s, 5p states.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Calculated partial and total density of states of Ag8SnS6.

The charge density has been studied, and it was used to analyze the electronic structure of the system. The charge density distribution of Ag₈SnS₆ in (040) plane is displayed in Fig. 4. The covalent bond of materials can be associated with the sharing of the electrons between the atoms. As seen in Fig. 4, there is a distinct continuity in the constant charge contours among Ag, Sn, S atoms. The charge accumulations are presented between S and Ag, Sn atoms. These indicate that covalent bonds are formed between Ag and S atoms, Sn and S atoms.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Charge density of Ag8SnS6 in (040) plane.

The dielectric function is used to describe the optical properties of solid material. The dielectric constant ε is given by

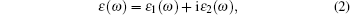where ε ₁ and ε ₂ are the real and imaginary part of the dielectric function, respectively. The ε ₂(ω ) can be used to describe the detail of the transitions between occupied and unoccupied electronic states, and the adsorptive behavior of materials. It is given by ^{[15, 28]}

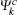
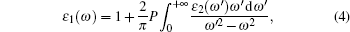where u is the vector defining the polarization of the incident electric field, r is the electron’ s radius vector, e is the electric charge, and are the wave functions of the conduction band and valence band, E is the incident photon’ s energy, and ε ₀ is the dielectric permittivity of vacuum. The real part of ε ₁(ω ) can be obtained by following the Kramers– Kronig relationship.^{[29, 30]}

where P is the principal value of the integral, defined as

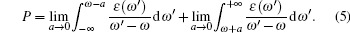The complex dielectric functions of different polarizations and polycrystalline are displayed in Fig. 5. Polycrystalline values are averaged over all polarization directions. The static dielectric constant ε ₁(0) is 4.15 at zero frequency limit. Because there is negative scale from 3.97 eV to 9.15 eV, it indicates that the Ag₈SnS₆ has a metallic behavior in these energy zones. As seen from Fig. 5(b), there are five peaks which are marked by the symbols A (2.89 at 1.96), B (3.08 at 2.64), C (8.05 at 3.51), D (2.34 at 6.40), and E (1.38 at 7.02). The peak A is due to the electronic transition from S 3s (at – 6.90 eV) to Ag 5s (at – 4.96 eV), S 3p (at – 4.85 eV to – 2.89 eV), S 3p (at – 6.91 eV) to Ag 5s (at – 4.96 eV), Sn 5s (at – 4.96 eV) to Ag 5s (at – 6.90 eV) and Sn 5p (at – 4.81 eV) to Ag 4d (at – 2.89 eV). Peak B is contributed from Sn 5p (at – 4.36 eV) to Ag 5s (at – 1.89 eV). Peak C is mainly due to the transition from S 3p (at – 6.91 eV) to Ag 5p (at – 3.46 eV) and Sn 5s (at – 6.90 eV) to Ag 5p (at – 3.46 eV). Peak D originates from S 3p (at – 6.91 eV) to Ag 4d (at – 0.54 eV), S 3s (at – 6.90 eV) to S 3p (at – 0.47 eV), S 3s (at – 6.90 eV) to Ag 4d (at – 0.54 eV) and Sn 5s (at – 6.90 eV) to Ag 4d (at – 0.54 eV). Peak E may be due to transition from Sn 5p (at – 12.10 eV) to Ag 5s (at – 4.96 eV) and Ag 4d (at – 12.16 eV) to Ag 5p (at – 4.96 eV).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Calculated dielectric function ε for Ag8SnS6 in different polarization and polycrystalline. (a) Real part ε 1(ω ); (b) imaginary part ε 2(ω ).

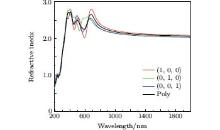
The refractive index n and Ag₈SnS₆ with different polarizations are presented in Fig. 6. The estimation of the refractive index is carried out by extracting square root of ε ₁(ω ) in the limit of infinite wavelengths. The static refractive index n(0) of three polarizations are as follows: n(1, 0, 0) = 2.08, n(0, 1, 0) = 2.03, and n(0, 0, 1) = 2.00, the gap between them is very small. The trend of these curves are the same, all of them have 3 peaks from 400 nm to 700 nm. The maximum n of (1, 0, 0), (0, 1, 0), and (0, 0, 1) polarizations are 2.80 at 683 nm, 2.80 at 404 nm, and 2.74 at 407 nm, respectively. The n(0) of polycrystalline is 2.04, and the maximum n is 2.72 at 405 nm.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Refractive index of Ag8SnS6 in different polarization and polycrystalline.

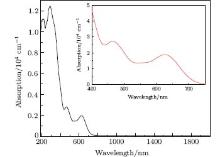
Ag₈SnS₆ is a significant photocatalyst, so the absorption coefficient is one of the most important parameters for measuring its catalytic activity. The calculated absorption spectrum of polycrystalline Ag₈SnS₆ is depicted in Fig. 7. It shows a wide absorbency from 190 nm to 750 nm, especially in the ultraviolet range (190– 400 nm), the absorption coefficient is almost above 8 × 10⁴ cm^{− 1}. It also shows a good adsorption in the visible light area (400– 750 nm), and the absorption coefficient locates at about 1 × 10⁴– 1.5 × 10⁴ cm^{− 1}. Comparison with the absorption spectrum of experiments in Ref. [9], the curves of these two spectrums have the same tendency in visible light area. However, the experimental data indicated that it has a weak absorption in the infrared region from 750 nm to 1350 nm. This difference might be related to the experiment conditions, the spectra were obtained by testing the nanocrystalline Ag₈SnS₆, while the calculation results were carried out by using the bulk Ag₈SnS₆. However, this evidence can explain that Ag₈SnS₆ has a marked catalysis activity under visible light radiation.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Absorption spectrum of Ag8SnS6.

As seen in Fig. 8, the optical conductivity σ (ω ), loss function L(ω ), and reflectivity R(ω ) are displayed. Optical conductivity of a semiconductor is associated with the change in conductivity caused by illumination, either an increase or a decrease. Generally, the optical conductivity is the physical basis of optoelectronic applications of semiconductors. It contains the absorptive σ ₁(ω ) (real part) and reactive σ ₂(ω )(imaginary part) current response to a time-varying external electrical field of frequency. The optical conductivity σ (ω ) is displayed in Fig. 8(a). The real part of optical conductivity is zero when the energy is less than 1.46 eV and greater than 11.39 eV, and the peak is 3.52 fs^{− 1} at 3.60 eV. In the imaginary part, σ ₂(ω ) value is zero at 7.56 eV.

Fig. 8.

	Figure Option ViewDownloadNew Window
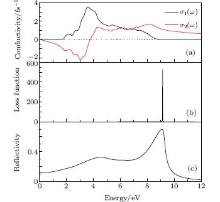	Fig. 8. Optical spectrum of Ag8SnS6. (a) Optical conductivity. (b) Energy loss function. (c) Reflectivity.

The loss function is a significance parameter describing the energy lost by an electron passing through a homogeneous dielectric material. The peak of loss function spectrum relates to the plasma resonance, and the corresponding frequency is called plasma frequency ω _p. Figure 8(b) shows that the resonant energy locates at 9.25 eV. The reflection coefficient can be obtained for the simple case of normal incidence onto a plane surface by matching both the electric and magnetic fields at the surface. Reflectivity R(ω ) is shown in Fig. 8(c). The R(0) is 11.5%, and the maximum reflectivity value is 66.10% at 9.08 eV. The Ag₈SnS₆ has a good reflective ability in the ultraviolet and visible light area (190– 750 nm). The small value of reflectivity as well as absorptivity in the infrared region indicates that Ag₈SnS₆ is transparent in this range.

The photocatalytic reactions occur at the surface of Ag₈SnS₆ nanocrystal. So the surface energy is an important factor to influence the photocatalytic activity. The surface energy is the energy required to create a new surface, and it is difficult to measure in the experiment. Generally, the surface energies are determined at the melting temperature. In the calculation, the surface energy γ can be calculated by taking the energy difference between the total energy of a slab and a bulk reference amount

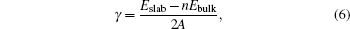where E_slab and E_bulk are the total energies of slab and bulk per unit cell, respectively, n is the number of unit cells in slab, and A is the surface area.^[31]

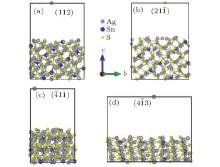
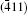
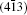
As seen from the literature, the nanocrystalline Ag₈SnS₆ have a submicropyramids structure, and its four outer faces correspond to , , , and (112) planes. These four surfaces were constructed by cleaving on the planes (Fig. 9). Firstly, the GGA and LDA exchange correlation functional were performed for determining E_bulk. The energies of slab were carried out using the same parameters as E_bulk calculation. The surface energies were calculated by using Eq. (6). The results are shown in Table 3. Experimental values of Ag₈SnS₆ surface energies have not been reported up to now. So we compared our presented GGA and LDA values with the calculated results from literature. It can be seen from Table 3, the surface has the maximum surface energy of 2.76 J/m² with GGA calculated and 3.02 J/m² with LDA. The with PBE and LDA calculations had the minimum energy of 1.11 and 1.42 J/m², respectively. The GGA calculation results seemed to underestimate surface energies. The LDA values were about 0.25 J/m² larger than PBE. Presented work surface energies were quite different from literature results. This might relate to the different module and different parameters used in simulation. The Dmol3 module was performed in the surface energies calculation in Ref. [9]. As reported in Ref. [17], a conclusion that LDA was the better choice of exchange correlation functional than GGA for surface energies calculation was obtained, because the LDA results were closer to experimental values.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Surface models of (a) (112), (b) , (c) , and (d) orientation of Ag8SnS6.

Table 3.

Table 3.

Table 3. Surface energies (J/m2) and work functions (eV) of Ag8SnS6 four different surfaces.     (112)   GGA 1.59 1.11 2.76 1.46 Surface energy/J· m– 2 LDA 1.80 1.41 3.02 1.84   Ref. [9] 2.16 0.74 0.83 1.31 Work function/eV GGA 4.706 4.559 4.415 4.524   LDA 4.874 4.663 4.604 4.733

Table 3. Surface energies (J/m2) and work functions (eV) of Ag8SnS6 four different surfaces.

The work function is the minimum energy required removing an electron from a solid to a point immediately outside the solid surface, or the energy needed to move an electron from the Fermi energy level into a vacuum. The expression is shown as follows:

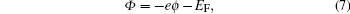where Φ is work function, – e is the charge of an electron, ϕ is the electrostatic potential in the vacuum near the surface, and E_F is the Fermi level inside the material.^[32]

Usually, this energy depends on the orientation of the crystal; different orientation surfaces have different work function values. As we know, in the photocatalytic reaction, the first step is that electrons move outside from the Ag₈SnS₆ surface under the light radiation. The mechanism can be expressed as follows: Ag₈SnS₆ + hv → e^– . Therefore, the work function is a significant parameter for estimating the catalytic activity of Ag₈SnS₆. Experimental and calculated work function values of Ag₈SnS₆ have not been reported yet. As seen from Table 3, GGA and LDA values were determined. The results of all four orientations were approximately at 4.5 eV. These values have little difference between each other. The surface has the minimum work function of 4.415 eV, and the surface has the maximum value of 4.706 eV with GGA evaluated. In LDA calculation, these two surfaces’ work functions are 4.604 and 4.874 eV, respectively. As for the surface energies, the work function values with LDA are bigger than GGA, and the LDA results are closer to the actual values. The LDA exchange correlation functional is a good choice for surface energy and work function calculating. These calculation values can be used as a reference for determination of experimental values.