Understanding the properties of normal state is believed to be key to unveiling the pairing mechanism in high-T_c superconductors. In both high-T_c cuprates and iron-pnictides, superconductivity emerges when the magnetic ordering is suppressed by additional charge doping or by an applied pressure.^{[1– 3]} This phenomenon has stimulated considerable studies on the magnetic property and its relation to superconductivity. Recently, another intriguing property of iron-pnictides was observed in the high temperature regime, namely the electronic nematic phase, in which the discrete lattice rotational symmetry is broken while the translational symmetry is retained. Experiments showed that iron-pnictides suffer a structural transition^{[4– 8]} at certain temperature T_S, across which the crystal symmetry changes from tetragonal to orthorhombic. Although the lattice deformation is very small ((a− b)/(a+b) < 0.01, with a and b denoting the in-plane lattice constants), sizeable electronic anisotropy has been observed in the in-plane resistivity measurements.^{[9, 10]} This so-called nematic character has also been identified in the optical conductivity spectrum, ^{[11– 13]} scanning tunnelling microscopy, ^{[14, 15]} and angle-resolved photoemission studies^[16] at a temperature even above T_S.

Currently, the nature of the nematic state as well as its relation to anisotropic magnetic couplings^[17] and the structural transition is a hot topic. Based on a spin-nematic scenario, ^{[18– 20]} anisotropic spin fluctuations above T_S have been taken as the driving force for the nematic state, and they induce the orbital polarization and drive a structural transition at a lower temperature T_S. On the other hand, in an orbital order scenario, ^{[21– 24]} a spontaneous breaking of the degeneracy between 3d_xz and 3d_yz orbitals is considered to be responsible for the nematic instability. The resulting unequal orbital occupations lead to anisotropic magnetic couplings and trigger a magnetic transition at a lower temperature T_N. While quite a number of experimental phenomena have been explained by either of the two scenarios, ^{[20, 25]} some important issues still need to be addressed. For instance, in the orbital order scenario, both calculated anisotropy in Drude weight^[22] and anisotropic orbital occupations^[26] showed the opposite sign to the experimental observations. Therefore, a unified physical picture is needed to clarify these anisotropic properties in the nematic state.

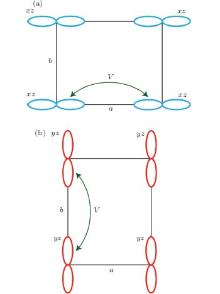
In our previous variational Monte Carlo (VMC) calculations, ^[27] we demonstrated that the nematic state can arise in a three-orbital model when a realistic off-site Coulomb interaction V is considered, which is the first time that the role of V in the formation of nematic state in iron-pnictides is identified. Here, we extend our work to a more realistic five-orbital model.^[28] In this five-orbital model, two iron 3d e_g orbitals are included in addition to the three iron 3d t_2g orbitals. Although these two e_g orbitals do not contribute significantly to the density of states close to the Fermi level, their strong hybridizations with the three t_2g orbitals give a better fitting to the bands obtained by the density functional theory. Moreover, in this five-orbital model, the π -bond like nearest-neighbor (NN) hopping is much stronger than the σ -bond one, leading to distinct NN hoppings between five- and three-orbital models (see Fig.  3). This is consistent with the first-principles Wannier function analysis^[21] and we will show that it is important for providing a unified physical picture in which the nematic state, the orbital order, and the anisotropic magnetic couplings are all associated.

The rest of the paper is organized as follows. In Section 2, the model and the variational Monte Carlo method are introduced. In Section 3, we present the main results and discuss the relations between the orbital, spin, and structure degrees of freedom. Conclusions of this paper are given in Section 4.

We start from the following five-orbital model on a two-dimensional square lattice:

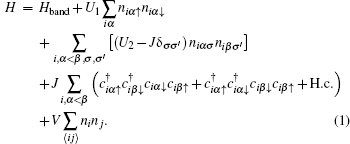The first term of the Hamiltonian reads

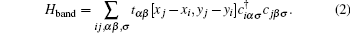The hopping integrals used here are from the Graser et al. paper, ^[28] in which the orbital basis is aligned parallel to the NN Fe– Fe direction rather than the Fe– As direction; this is convenient for investigating the nematic state in which the two orthogonal Fe– Fe directions are non-equivalent. Another important feature is that the σ -bond like NN d_xz– d_xz hopping along the x direction is much weaker than the π -bond like one along the y direction, e.g., | t_{xz, xz} [1, 0]| ≪ | t_{xz, xz}[0, 1]| , and for the d_yz orbital. This is due to the strong deformation of the orbitals induced by the hybridization between Fe 3d and As 4p orbitals.^[21]

The interaction part of the model includes the intraorbital and interorbital Coulomb interactions U₁ and U₂, the Hund coupling J, as well as the Coulomb interaction V between the NN sites. The interacting parameters are U₁ = 2.0, U₂ = 1.0, and J = 0.5 in units of eV in this paper unless otherwise stated, which correspond to the typical values of iron-pnictide superconductors.^{[29– 31]} In our previous work, we demonstrated that the nematic state is not stable unless V is larger than a critical value V_c = 0.33.^[27] In this paper, we vary V from 0.0 to 0.4.

We describe the nematic state by introducing an anisotropic hopping order (AHO) with order parameter δ _var. This kind of introducing the nematic state has successfully captured the nature of the nematic state in high-T_c cuprates.^{[32, 33]} A non-interacting variational Hamiltonian H_MF is then obtained by substituting the hopping integrals t_{α β} [Δ x, 0] and t_{α β} [0, Δ y] in H_band by the effective hopping integrals

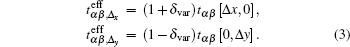The wave function | Ψ _MF〉 is obtained by diagonalizing the quadratic Hamiltonian H_MF. The projected wave function we use in VMC is then constructed as follows:

where

Here g₁, g₂, and g_J are the variational parameters controlling the number of electrons residing in the same and the different on-site orbitals, and g_V controls the number of electrons on the NN sites. It is well-known that the ground state of iron-pnictides is an antiferromagnetic (AFM) state at low energy, while in this paper, we will focus on the nematic state in the high temperature paramagnetic regime. We are interested in the microscopic mechanism of the unusual anisotropy in the tetragonal crystal structure.

The VMC simulations are carried out on 10× 10 and 14× 14 lattices with periodic boundary conditions along the x and the y directions. We define N as the number of sites and n as the average number of electrons per site. In this paper, we investigate the undoped case with n = 6. The ground-state energy 〈 ψ | H| ψ 〉 is calculated using a standard Markovian chain Monte Carlo approach with the Metropolis update algorithm, ^{[34– 37]} and it is optimized with respect to the variational parameters. During the optimization, a quasi-Newton method combined with a fixed sampling method^{[38, 39]} is used. In the figures presented below, the statistical errors are smaller than the symbol sizes unless otherwise stated.

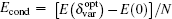
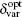
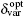
Firstly, the condensation energy per unit cell and the optimized AHO parameter as a function of V are presented in Fig.  1. One can see that E_cond and are zero when V is less than a critical value V_c = 0.30 in the 10× 10 lattice (0.32 in the 14× 14 lattice). For the three-orbital model, the critical value V_c is estimated to be about 0.33, ^[27] which is close to the value obtained for the five-orbital model. These results provide conclusive evidence that the off-site Coulomb interaction V plays a key role in forming the nematic state in iron-pnictides. The error bar (not shown) in Fig.  1(b) is about 0.05, which is due to the finite size effect, manifested as a discontinuous change of the Fermi surface when the variational parameter δ _var changes continuously.^[27]

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Condensation energy Econd and (b) optimized δ var as a function of V.

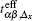
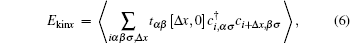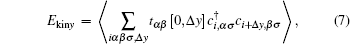Due to the development of AHO, the effective hopping integrals and defined in Eq.  (3) become anisotropic. As a result, the kinetic energies along the x and the y directions, which are defined as

become anisotropic, as shown in Fig.  2(a). The decrease (increase) of E_kinx (E_kiny) as a function of δ _var will result in a stronger anisotropy of the kinetic energy as the nematicity is enhanced. This behavior is very similar to the one observed in the three-orbital model.^[27] As already discussed in our previous work, ^[27] the derived optical conductivity and Drude weight contain the terms that are closely related to the hopping integrals and the hopping processes of electrons. The anisotropic kinetic energy, which is obtained from the kinetic (hopping) terms in Eq.  (2), suggests that the calculated x and y components of the optical conductivity and the Drude weight in the nematic phase are unequal, resulting in anisotropic optical and dc conductivities as observed in Ba(Fe_{1– x}Co_x)₂As.^[13]

The anisotropic effective hopping integrals also lead to the anisotropy of electron occupations in the d_xz and d_yz orbitals, as shown in Fig.  2(b). While the d_yz orbital occupation n_yz decreases and approaches half-filling, the d_xz orbital occupation n_xz increases monotonically as δ _var is increased. This kind of anisotropic electron occupation is opposite to the one in the three-orbital model.^[27] As shown in Fig.  3(a), the leading d_yz– d_yz and d_xz– d_xz hopping integrals in the five-orbital model are along the x and y directions, respectively, while the two leading hopping integrals are reversed in the three-orbital model (see Fig.  3(b)). 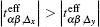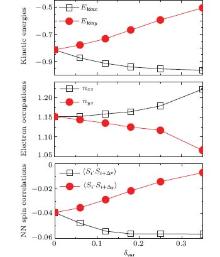In the nematic state with , n_xz > n_yz or n_xz < n_yz is developed to benefit the kinetic energy in the five- or three-orbital model due to the different leading hopping processes. The orbital order obtained in this work is in agreement with the experiment, ^[16] where it was found that as the temperature is lowered toward T_N, the shift up and shift down of the d_yz and d_xz bands lead to larger occupation of the d_xz orbital.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Kinetic energies, (b) electron occupations in the dxz and dyz orbitals, and (c) NN spin correlations as a function of δ var at V = 0.36 on the 14× 14 lattice.

The physical picture of anisotropic NN magnetic couplings^[17] driven by the orbital order has already been proposed by Lee et al.^[21] In their picture, the d_xz orbital is almost doubly-occupied, while the d_yz orbital is almost singly-occupied and spin-polarized. As the d_yz– d_yz hopping along the x direction is much stronger than that along the y direction, anisotropic spin superexchanges with J_x > J_y are naturally obtained. Our results shown in Figs.  2(b) and 3(a) are in qualitative agreement with Lee et al.’ s analysis, therefore anisotropic NN magnetic couplings can be realized in the nematic state, which leads to the anisotropic magnetic properties shown in Fig.  2(c). One can see that in the normal state (δ _var = 0), the NN spin correlations along the two directions have the same negative value. When the nematicity develops (δ _var > 0), the spin correlation along the y direction approaches 0, while the one along the x direction is enhanced.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The leading hopping integrals along the x and y directions in (a) the five-orbital model and (b) the three-orbital model.

Having identified the microscopic origin of the nematic state and the induced orbital order, we now turn to the instability of the structural transition with a > b, which was observed by experiments.^{[4– 6]} As shown in Fig.  4(a), the shape of the d_xz orbital combined with the dominant d_xz electron occupation prefers a lattice distortion with a > b, since the repulsive energy caused by the NN d_xz– d_xz off-site Coulomb interaction can be dramatically reduced. On the other hand, for dominant d_yz electron occupation, a lattice distortion with a < b is preferred, as displayed in Fig.  4(b). In the nematic state, we have unequal electron occupations with n_xz > n_yz as shown in Fig.  2(b), so the experimentally observed lattice distortion with a > b is obtained. From this physical picture, one can see that the off-site Coulomb interaction V not only plays a key role in the formation of the nematic state, but also contributes to the structural transition, across which the crystal symmetry changes from tetragonal to orthorhombic.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Schematic diagram of the contributions of the orbital order to the structural distortion: (a) dominant dxz occupation prefers a structural distortion with a > b; (b) dominant dyz occupation prefers b > a.

Our VMC study demonstrates that the nematic state is stable in the realistic five-orbital model when the off-site Coulomb interaction V is larger than a critical value V_c ≈ 0.30 . Miyake et al.’ s ab initio calculations^[40] indicated that the typical value of V is about 0.50 ∼ 0.90 in iron-pnictides, which is much larger than V_c, therefore, the nematic state can be realized in actual materials. The development of nematicity results in unequal electron occupations with n_xz > n_yz and anisotropic magnetic couplings with J_x > J_y, which are consistent with the ones observed in experiments. The resulting anisotropic kinetic energies are closely related to the experimentally observed anisotropic optical and dc conductivities. In addition, we find that the inclusion of the off-site Coulomb interaction V is crucial for the structural distortion with a > b.

In our work, the nematic state is introduced by AHO, and the orbital order and the anisotropic spin correlations are the consequents of the development of AHO. Thus, we do not disentangle the roles of orbital degree of freedom and spin degree of freedom in the formation of the nematic state. Further works that directly describe the nematic state in the form of orbital order or spin order are needed. The question of which one is the dominant degree of freedom will be answered when comparing the calculated results to the experimental measurements.