The iron-based superconductors have drawn great attention since their discovery, ^[1] especially because of their transport properties. Some iron-based superconductors display good potential for practical applications, e.g., the superconductivity of A_0.8Fe_1.7Se₂ series possess excellent sustainability under high magnetic field. Thus, it is especially important and necessary to study the vortex dynamics of the iron-based superconductors to obtain better application.

As we know, the vortex dynamics of a traditional s-wave superconductor can be well described by the Kim– Anderson model.^{[2, 3]} While the vortex behavior of cuprate superconductors usually fit the vortex-glass (VG) model.^{[4, 5]} The VG model suggests a phase transition from the vortex liquid phase to the vortex solid phase once the temperature drops below T_M, where T_M is defined as the vortex glass transition temperature. The suitability of the VG model has been testified in various superconductors such as YBCO, ^{[6, 7]} Tl₂Ba₂CaCu₂O₈, ^[8] and MgB₂.^[9] However, there have been arguments over the suitability of the VG model for iron-based superconductors recently.^[10] To study the vortex dynamics of iron-based superconductors, we choose a typical layered compound Tl_0.4K_0.41Fe_1.71Se₂ single crystal as the subject.

In this paper, we fabricate high-quality Tl_0.4K_0.41Fe_1.71Se₂ single crystals. We examine I– V curves of Tl_0.4K_0.41Fe_1.71Se₂ single crystal around T_C under a magnetic field as high as 10 T, yet have trouble understanding it with the vortex glass model. We give explicit and reasonable explanations of the phenomenon.

Single crystals of Tl_0.4K_0.41Fe_1.71Se₂ are prepared through the self-flux method. The details have been reported elsewhere.^[11] The crystals are shiny on the surface and easy to cleave off the mixture. The sample dimensions are measured to be 5× 7.17× 0.05 mm³. The superconductive transition width is within 0.4 K, reflecting the excellent quality of the single crystal. The intersecting point of linear extrapolating lines from the normal state and the steep transition area gives T_C = 30.63 K. The I– V and ρ – T tests under less than 300 K are taken using a four-probe method on a PPMS device (Quantum Design), with various magnetic fields applied perpendicularly and parallel to the sample. The current flow is confined within the ab plane of the sample.

During the I– V measurement, the sample’ s surrounding temperature might be raised due to Joule heating. In order to limit this temperature lift, on one hand, the shape of the sample is chosen properly to obtain a rather small resistance; on the other hand, the maximum of current is strictly controlled (below 200 mA). All the curves used in the final scaling have temperature ranges within 0.1 K. Measurements on several different samples from the same batch lead to similar results.

The angle between the sample and the magnetic field is decided as follows. We apply a 1 T field to the sample and find the middle point of the superconductive transition. Then we fix the temperature to this point, and precisely measure the resistivity while the angle is changed from 0° to 360° . Angles at which the resistivity values reach extrema correspond to the orientations where the field is applied perpendicularly and parallel to the ab plane.

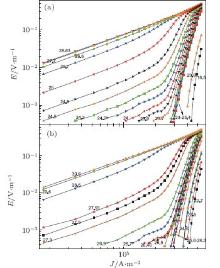
The E– j isotherms under the magnetic field of 10 T are presented in Fig. 1. We calculate the glass correlation length ξ ₀^[16] to decide whether to use the quasi-two-dimensional (2D) or the 3D scaling. We obtain a value of 970 Å under 10 T (our result of ξ ₀ gradually increases with increasing field, as reported previously), which is certainly large enough to indicate the 3D behavior. According to the vortex-glass theory, one should be able to get the power exponent law of E versus j near T_M, i.e., E(j, T) ≈ j^{(z+ 1)(d− 1)}, where z is the dynamic critical exponent, d is the dimension, and T_M is defined as the vortex-solid melting transition temperature. From empirical law, we know that U(j) ∝ 1/j^μ , where U(j) is the thermal activation energy, while μ is the power exponent. When j → 0, the activation energy U(j), i.e., the potential barrier, increases to infinity. Thus, the linear resistivity (ρ _lin) vanishes upon the appearance of a vortex-glass phase when the temperature drops below T_M. 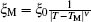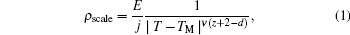We might define the vortex correlation length ξ _M and relaxation time τ _M as and τ _M = ξ ^z, where ν is the static exponent. According to the VG theory, with appropriate values of T_M, z, and ν , the isotherms could be diverged into two branches, i.e., E₊(T > T_M) and E_– (T < T_M). The value of ν could be deduced from the behavior of ρ _lin, as ρ _lin ≈ (T − T_M)^{ν (z+ 2− d)} before vanishing. Through defining

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The j dependence of E in double logarithmic coordinate. (a) E– j curves measured at various temperatures under a 10 T magnetic field applied perpendicularly to the ab plane. (b) E– j curves measured at various temperatures under a 10 T magnetic field applied parallel to the ab plane.

and

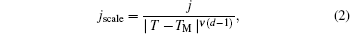we should be able to complete the scaling for the two magnetic field orientations.

As can be seen from Fig. 1, it is difficult to find an absolute straight line in the logarithmic coordinate, as predicted by the VG model. There is no existence of the absolute “ vortex liquid phase” and “ vortex solid phase” that the VG theory predicts, and thus no proper T_M value to perform the universal scaling. This clearly indicates that in this case, the VG theory is unable to describe the vortex dynamics of Tl_0.4K_0.41Fe_1.71Se₂.

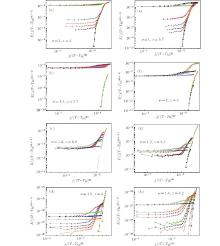
We try ergodic T_M values in our measuring interval, and adjust the values of the two exponents z and ν . However, it is still unable to obtain a decent scaling for present data. Some of the best scaling results available are shown in Fig. 2. One can see that when the T_M value decreases, the curves begin to display severe disorder in the high-dissipation region. On the other hand, obvious divergence emerges in the lower branch when T_M value increases. It is worth mentioning that the temperature lift due to the Joule heating becomes severe at low temperature. In order to exclude the possibility that proper T_M values might exist at temperatures lower than the measuring ranges, we also try to scale with T_M at low temperatures down to 4 K, without decent results. The results at 4 K are shown in Figs. 2(d) and 2(h). This clearly indicates that in this case, the VG theory is unable to describe the vortex dynamics of Tl_0.4K_0.41Fe_1.71Se₂.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The best scaling obtained with TM set as (a) 25 K, (b) 23.7 K, (c) 22 K, (d) 4 K under a 10 T magnetic field applied perpendicularly to the ab plane. The best scaling obtained with TM set as (e) 28 K, (f) 26.2 K, (g) 25 K, (h) 4 K under a 10 T magnetic field applied parallel to the ab plane.

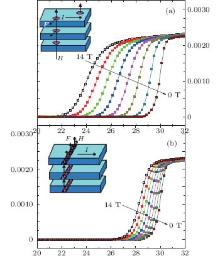
The reason could be retraced to the establishment of the VG theory. Without different treatments for the different layers of the compounds, the VG theory was built to describe the cuprates, which could be treated as homogeneous anisotropic superconductors. However, the Tl_0.4K_0.41Fe_1.71Se₂ single crystal might not be the case here. The Tl_0.4K_0.41Fe_1.71Se₂ compound has a layered structure with intercalating Tl(K) layers and FeSe layers. The FeSe layers are superconductive, while the Josephson junction region (Tl(K) layers) could also be superconductive as a result of the proximity effect. However, the superconductivity is very weak compared to the strong superconductive FeSe layers, and therefore, much easier to undergo the transition to the normal state. Could such a compound still be treated as a homogeneous one? In order to clarify this, we measured the temperature dependence of resistivity under different magnetic fields perpendicular and parallel to the ab plane, as shown in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Temperature dependence of the resistivity for Tl0.4K0.41Fe1.71Se2 single crystal under magnetic field of μ 0H = 0, 2, 4, 6, 8, 10, 12, 14 T applied (a) perpendicularly and (b) parallel to the ab plane.

Similar curves have been seen in the case of Bi₂Sr₂CaCu₂O₈; ^[12] the broadening in the low-temperature region was well explained by the flux creep behavior, within the framework of the Anderson– Kim flux creep model. Zeldov et al. relates the broadening to the existence of a logarithmically shaped flux line potential well, ^[13] as he did to YBa₂Cu₃O₇ films.^[14] For the alternative, Chen et al. described the phenomenon with the bipolaron theory.^[15] For the present data, the pinning is not as strong as in cuprates, and the pinning force could be overshadowed by the driving force under high magnetic fields. Therefore, sole consideration of the flux creep behavior is insufficient, and the effects of flux flow motion must be included. It could be easily observed that the resistivity display dramatic contrasting behaviors with different field orientations, as a result of the material’ s structure and vortex mechanisms. 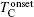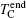Take the curves corresponding to the 14 T field for example, values vary as much as 5.1 K, while values vary 4.0 K. This cannot be attributed to a simple anisotropy. It is well known that when the field is applied perpendicularly to the ab plane, the vortices exist in the form of 2D “ pancakes” . The pancake vortices in the same layer repel each other, and the ones in adjacent layers attract each other via Josephson coupling.^[16] Here the Josephson coupling constitutes the pinning force (F_P) for the pancake vortices. The ascending temperature makes the pinning of vortices less effective and the pancakes begin to move under the drag of Lorentz force (F_L). This motion causes the energy dissipation, and therefore, the electrical resistance, as shown in Fig. 3(a). The gradual increase of resistivity indicates the recovery process of the weak superconductive region (Tl(K) layers) into the normal state. Upon this recovery, the flux lines connecting pancake vortices are broken, thus pancakes start to move independently in the superconducting layers. This is when the superconducting layers begin their recovery. This process corresponds to the long tailed resistance increase (see Fig. 3(a)).

On the other hand, when the field is applied parallel to the ab plane, an orthogonal elongated lattice of elliptical vortex strings forms. Here the F_L is perpendicular to the ab plane, thus the vortex must cross the Josephson junction region. In this case, the weak inter-layers, i.e., the Josephson junction region would act as barriers which hinder the motion of the vortex. At low temperatures, the strong pinning overshadows the F_L, thus the vortex cannot climb over the barrier. With ascending temperature, the thermal fluctuation offers extra energy, which leads to the recovery of the superconducting layers into the normal state. Thus, what we see is a sudden and sharp transition, in great contrast with the slow recovery in the H ⊥ ab-plane case.

One thing that has to be particularly noted for Tl_0.4K_0.41Fe_1.71Se₂ is that its superconducting shielding volume is very small, which only composes 20%– 30% of the total volume. Its inhomogeneity exists not only between different orientations, but also amongst the same layer. Abundant experimental evidence has proven the A_xFe_{2− δ} Se₂ series to be a phase-separated system.^{[17– 19]} Take the compound K_xFe_{2− δ} Se_{2− y} for example, four phases in all have been detected, including the parent compound KFe₂Se₂ with charge ordering, the superconducting KFe₂Se₂ with charge ordering, the superconducting KFe₂Se_2-y with Se vacancies, and insulating K₂Fe₄Se₅ with Fe vacancy order.^[20] Inhomogeneous distribution of the phases would cause obstruction of the superconducting channel along the ab plane, with a typical scale below 1 μ m. The inter-layer case is similar, which displays contrasting difference from the cuprates.

As we could see from above, the Tl_0.4K_0.41Fe_1.71Se₂ superconductor is not a homogeneous material at all, the two distinct types of layers display two totally different superconductive phases. Whether the vortices (vortex) have (has) to cross the Josephson Junction region makes a huge difference. Considering the important role the Josephson junction region plays in the superconductor’ s recovery process, its composition of the two different types of layers cannot be treated as the simple anisotropy in a homogeneous compound as the VG theory does. In contrast with the case in Tl_0.4K_0.41Fe_1.71Se₂, the difference between the Josephson junction region and strong superconductive layers could almost be ignored in some HTSCs, e.g., Bi-based cuprates (BSCCO). Except for the tail effect caused by the flux creep, its temperature dependence of resistivity behaviors are almost identical under different field orientations.^[21] As predicted by the VG theory, its I– V curves could be neatly scaled.^[22]

From another perspective, the reason why the VG model cannot explain our experiment results could be understood mathematically. As the VG theory gives

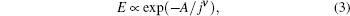where ν ≤ 1 in the VG theory, while ν = 1/7, 3/2, 7/9, 1/2 in the collective pinning model, and A is irrelevant to j. Thus, we have ln E ∝ − A/j^ν in the logarithmic coordinate. The curvature of the model is easy to obtain

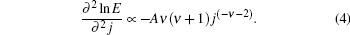Once the value of A is fixed, the curvature would not be able to change its sign for the same isotherm. Consequently, the model is unable to describe the isotherms, which change curvature signs between T₋ and T₊ in our experiment.

In conclusion, we report the measurement of current– voltage characteristics for our high-quality Tl_0.4K_0.41Fe_1.71Se₂ single crystal. We choose varying T_M values and adjust scaling exponents accordingly in the hope of obtaining a universal scaling. However, we cannot find a proper isotherm for T_M as the VG model predicts, also the ln E– ln j curves cannot be scaled neatly into two branches. Through analysis of the temperature dependence of resistivity under fields with different orientations, we find one major difference between A_0.8Fe_1.7Se₂ and HTSCs. In the A_0.8Fe_1.7Se₂ compound, the strong superconductive FeSe layers and the Josephson junction region (Tl(K) layers) display two distinct types of superconductive phases, as they behave entirely differently from each other in the compound’ s recovery from the superconductive state to the normal state. Thus, it would be improper to treat it as a simple homogeneous anisotropic superconductor as the VG theory does; while HTSCs fit well into this approximation, which enables them to be nicely described by the VG model. Thus, we propose that the series of A_0.8Fe_1.7Se₂ superconductors might provide a new convenient platform to study the complex vortex behaviors in the layered superconductors and perfect the existing models, or even build up new ones.