Corresponding author. E-mail: ytli@iphy.ac.cn
Project supported by the National Basic Research Program of China (Grant No. 2013CBA01501) and the National Natural Science Foundation of China (Grant No. 11135012).
The remarkable experimental progress in the studies of collisionless shockwave (CS) in laboratories employing high-power lasers is briefly reviewed. The results show that CS can be generated in laser-produced plasmas due to the micro-turbulence associated with instabilities. CS is one of the most important astronomical phenomena. It has been found in supernova remnants (SNRs), Sun–Earth space, etc. This paper focuses on CS in ways relevant to SNRs. Laboratory astrophysics (LA), a new interdisciplinary frontier of astrophysics, plasma and laser physics, has developed rapidly in recent years. As an accessory to the astronomical observation, LA experimenters can closely study some astronomical events scaled-down to controllable phenomena.
With the development of the high energy density (HED) facilities, such as high power lasers[1– 3] and Z-pinch machines, [4, 5] one can create extreme physical conditions in the laboratory. This allows us to build controllable and repeatable experimental test-beds to investigate some astrophysical processes. Although the spatial and temporal scales of laboratory plasmas are very different from the astrophysical ones, the similarity criteria proposed by Ryutov et al. allow a direct scaling between them, in which the variables of the systems remain invariant under a transformation.[6, 7] This keeps the physical processes of both systems the same or similar. Those progressive steps promote a new research field – - laboratory astrophysics (LA).[8] LA includes many research topics, such as collisionless shockwave (CS), [9, 10] magnetic reconnection (MR)[11, 12] jets and outflows.[13, 14] Compared with the traditional astronomical observation and theoretical simulations, studies in a laboratory are positive, controllable, and near-distance. It has become a new option to investigate some important astronomical phenomena.[15– 18]
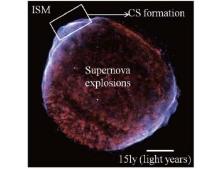
In this paper, we focus on the CS generation in the laboratory with applications to supernova remnants (SNRs).[19, 20] General reviews of LA can be found in Refs. [21]– [23]. CS is a common phenomenon in SNRs. It generally results from fast-moving counter-streaming plasma systems, formed by interaction of the fast mass ejections from supernova explosions with the surrounding interstellar medium (ISM). Because the particle density is very low throughout the ISM and the velocity of the ejections is very high, the mean free path (MFP) is typically larger than the shock transition region. Therefore, most shockwaves observed near SNRs are collisionless. Figure 1 shows an X-ray image of supernova (SN) 1006, taken by the orbiting Chandra Observatory in 2005. The huge puff ball is the supernova explosion and the sharp edge is the shock front. According to the astronomical observation, [24] the diameter of SN 1006 is about 70 light years and it continues to expand. The temperature at the shock front is Ti ∼ 15 keV and the density is ni ∼ 1cm− 3, the corresponding MFP is estimated to be 4× 1019cm. However, the shock front width is measured to be about 1.2 × 1017cm, which is much shorter than the MFP. This means that the shock is induced by the collisionless collective effect instead of collisions between ions.[25] Studies indicate that micro-turbulence associated with some instabilities can provide electromagnetic (EM) fields to sustain the shocks. Two instabilities are responsible for the shock formation: one is the electrostatic instability, [26] and the other is the Weibel instability, or current filamentation instability.[27] The corresponding shocks are called the collisionless electrostatic shockwave[28, 29] and the collisionless Weibel-mediated shockwave.[30, 31]
CS formation is accompanied by energy transformation. It is believed that high-energy particles and cosmic rays are related to CS. Particles can be trapped by the shock and accelerated to high energy.[32– 34] Depending on the acceleration process, two types of shockwave acceleration (SA) can occur: shock drift acceleration (SDA)[35] and diffusive shock acceleration (DSA).[36] SDA is non-stochastic and depends on the particle motion in a specified EM field, while DSA is stochastic. Fermi acceleration, [37] an example of the stochastic acceleration, is a well-known model to explain the generation of cosmic rays. Recently, such cosmic particles from SNR were observed for the first time by NASA’ s orbiting Fermi Gamma-ray space telescope.[38] It provides evidence of the generation of cosmic rays by the CS from SNR. For CS and SA, several key questions remain unsolved. For example, how do the collective EM fields arise? How does the CS form the micro-turbulence? How does the CS accelerate the high energy particles? Laboratory experiments could be helpful to answer those questions in a scaled and controllable way. Here we report recent progress in studies of CS in the laboratory. The paper is organized as follows. In Section 2, the typical target configuration and the diagnostics used for CS generation in a laser-plasma experiment are introduced. In Section 3, the remarkable results and discussions of CS generation are reviewed. In Section 4, the summary and outlook are given.
Figure 2 shows a schematic view of the target configuration of CS generation. The whole target consists of two opposite foils, separated by distance L. The counter-streaming plasmas can be produced by either of two schemes. One is to use a bunch of laser pulses to irradiate a foil to blow out an incoming flow from the target’ s rear side. The counter-streaming flow is generated due to photoionization of the other target by the intense X-ray of the laser-irradiated target. This scheme has been used at the Gekko XII laser facility.[39] The other one is to use two bunches of laser beams to irradiate the facing surfaces of two foils to directly produce two counter-streaming plasmas. This scheme has been applied at multi-direction laser irradiation facilities such as Shenguang-II (SG-II) and OMEGA EP.
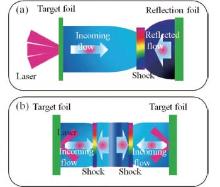 | Fig. 2. Schematics of CS generation with intense laser beams: (a) one-direction laser irradiation of targets (b) multi-direction laser irradiation of targets. |
Generating CS in the laboratory must satisfy the collisionless condition, [6] i.e., the MFP (λ ii) is larger than the shock transition (Ws). The MFP is expressed as 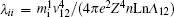

There are two typical imaging diagnostics for the interaction between the counter-streaming plasmas, as shown in Fig. 3. One is proton imaging, and the other is optical imaging. The proton imaging is sensitive to the electric and magnetic fields, so it can reveal the structures of the electric and magnetic fields in high energy density plasmas.[41] The optical imaging, in which an optical laser pulse is typically used as a probe beam, is sensitive to the plasma density, so it can give the plasma density.[42]
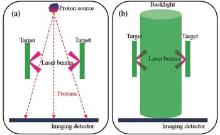 | Fig. 3. Schematics of (a) the proton image and (b) the optical image. |
As mentioned above, studies of CS in the laboratory are based on the similarity criteria proposed by Ryutov et al.[6, 7] In 2000, Drake[43] proposed that a laboratory experiment could be used as a new tool to investigate collisionless shocks of cosmic relevance. When some specific conditions are met, a cosmic shock can be driven by a kJ class laser facility. In 2004, Courtois et al.[44] studied the collisionless interaction between two counter-streaming plasmas produced by two opposite foil targets, which was scaled to the SNRs. In their experiment, the dynamics of the two plasmas and their interaction with and without an external magnetic field were diagnosed with optical imaging. The experimental results showed that the plasma density profiles are different in both cases, but there is no evidence of shock generation. Since 2006, a series of theories and particle-in-cell simulations[30, 31, 45, 46] have shown that a CS can be generated in counter-streaming plasmas without an external magnetic field. In the Sorasio et al. theory, [45] a very strong collisionless electrostatic shockwave can be generated when the counter-streaming plasmas with different properties (temperature, density, composition, etc) interact with each other. In Kato the et al. simulations, [30] a CS is mediated by a strong magnetic field, which results from the Weibel instability in the counter-streaming plasmas. The energy density of the magnetic field reaches approximately 1% of the streaming bulk energy density. In 2010, PIC simulations[46] aimed at understanding the electrostatic and electromagnetic instabilities in counter-streaming plasmas associated with shocks were carried out. The results demonstrated that an electrostatic shockwave is generated in the early stages, and then a Weibel-mediated shockwave follows.
In the same year, a China– Japan joint CS experiment[47] was performed at the SG-II laser facility. The counter-streaming plasmas were produced with a scheme similar to that shown in Fig. 2(a). The difference is that a bunch of laser pulses irradiates the inner surface of the left target foil to generate the incoming plasma flow. The diagnosis was accomplished by optical imaging, including interferometry and shadowgraphy. Figures 4(a) and 4(b) show the interferograms taken at delay times of 5 ns and 9 ns, and figures 4(c) and 4(d) show the corresponding shadowgraphs. A large density jump is observed at 9 ns. The width of the density jump (∼ 50 μ m) is much narrower than the MFP (1.2– 1.7mm). The experimental results and simulation analysis indicate that a collisionless electrostatic shockwave is generated in the counter-streaming plasmas.
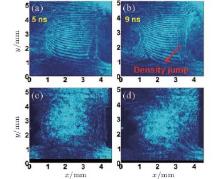 | Fig. 3. (a) Interferogram and (c) shadowgraph taken at a delay time of 5 ns. (b) Interferogram and (d) shadowgraph taken at a delay time of 9 ns.[46] |
The CS generation by the second scheme, shown in Fig. 2(b), was also demonstrated at the SG-II laser facility.[48] A series of interferograms obtained at delay times of 1 ns, 2 ns and 3 ns are shown in Fig. 5. A clear density jump from 8.1× 1018cm− 3 to 2.4 × 1019cm− 3 is observed at the middle region in Fig. 4(b). For a shockwave in a perfect gas, the density compression ratio can be expressed as ns/nb = (γ + 1)M2/((γ − 1)M2 + 2), where ns and nb are the shockwave density and the background density, γ is the adiabatic constant of the monatomic gas, and M is the Mach number of the shockwave. For a two-dimensional very strong (M ≫ 1) shockwave, the upper limit of the density compression ratio can be calculated as ns/nb = 3. From the experimental results, the Mach number is found to be approximately equal to 14, which indicates that a very strong shockwave was generated. Additionally, the dimensionless parameters of our experiment are compared with those of SNR, as shown in Table1. This indicates that it is feasible to study CS from SNRs in the laboratory.
 | Fig. 5. Interferograms taken at delay times of (a) 1 ns, (b) 2 ns, and (c) 3 ns.[47] |
| Table 1. Comparison of the dimensionless parameters of the shockwave in SNR with experimental ones at 2 ns.[47] |
In 2011, Kuramitsu et al.[49] investigated the time evolution of a strong collisionless shock in counter-streaming plasmas using the Gekko-XII laser pulses. Figure 6(a)shows the time-resolved interferogram measured by a streak camera, giving the time evolution of the counter-streaming plasmas. Simultaneously, streaked optical pyrometry (SOP) was used to measure the interaction. The result is shown in Fig. 6(b). The Mach number of CS is estimated to be 10 in two different diagnostics, indicating a very strong CS was generated.
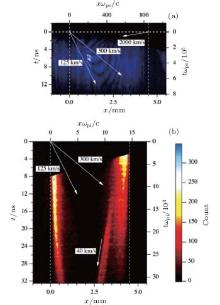 | Fig. 6. (a) Streaked interferogram. (b) Streaked optical pyrometry.[48] |
In 2012, large and self-organized electromagnetic field structures[50] were observed in the counter-streaming plasmas produced by the OMEGA EP laser facility. The fields were probed by a proton source. Figure 7 shows the evolution of the structures obtained by the proton imaging. Those structures persist for thousands of ion timescales and tens of thousands of electron-kinetic timescales. The measurements confirm that those structures are induced by the self-generated electromagnetic field. However, it is not clear how the macroscopic structures form the microscopic turbulence.
 | Fig. 7. (a)– (f) Evolution of the self-organized electromagnetic field structures.[49] |
The filamentary structures were observed using optical imaging during the high-speed counter-streaming plasmas interaction in 2009 and confirmed by follow-up experiments at the SG II laser facility.[51] Figure 8 shows the typical interferogram and shadowgraph taken at a delay time of 5.5 ns.[52] Some clear fine filaments appear at the middle region. The lengths of the filaments differ. The maximum length is about 464 μ m and the minimum is about 168 μ m. Two micro-instabilities are associated with the filaments.[46] One is the electrostatic instability and the other one is the Weibel-type instability. The length of the filaments induced by the electrostatic instability is scaled as 0.67c/ω pe = 5.3 μ m, which is much shorter than that of the filaments observed in our experiment. The typical length of the filaments induced by the Weibel-type instability is 42c/ω pe = 224 μ m. Although this is still shorter than that observed in our experiment, the filaments induced by the Weibel-type instability can coalesce to each other and become larger filaments with stronger magnetic fields until saturation.[53] It is possible that the filaments are induced by the Weibel-type instability. As far as we know, this is the first time the Weibel-type instability has been observed in an experiment.
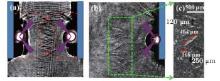 | Fig. 8. (a) Interferogram and (b) shadowgraph taken at a delay time of 5.5 ns.[51] (c) Enlarged image corresponding to image (b).[51] |
In 2013, Fox et al.[54] observed the filaments induced by the Weibel instability using proton imaging. Figure 9 shows the proton images of the evolution of filaments in counter-streaming plasmas. As mentioned above, the proton imaging can reveal the structure of the electric and magnetic fields. In the experiment, a strong magnetic field of about 50 T was induced by the Weibel instability. This was the first time the strength of the magnetic field induced by the Weibel instability in non-relativistic counter-streaming plasmas was measured.
 | Fig. 9. (a)– (c) Development of the Weibel-type instability.[53] |
This paper briefly reviews the remarkable experimental progress in CS driven by high-power laser pulses in the laboratory. Strong collisionless electrostatic shockwaves and the filaments induced by the Weibel instability have been demonstrated in laser-produced counter-streaming plasmas. The experimental results help us understand how collisionless shockwaves are produced, and these results may be scaled to the SNR. However, further work is needed to understand the Weibel-mediated shock formation and how the particles are accelerated by the CS.
Future experimental work will employ much higher laser energy to excite stable and strong Weibel-mediated shocks and improve the diagnostics to help measure the topological structure of the magnetic field induced by the Weibel instability and the energy spectrum of the accelerated particles. The National Ignition Facility (NIF), Laser MegaJoule (LMJ), and the SG III laser facility make such high energy density experiments feasible.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|