Absorption of lasers in laser– matter interactions is an important issue, which has been attracting continued interest ever since the invention of lasers. In the case with high power lasers, laser absorption is closely related to the applications of laser– plasma interactions, which include the inertial fusion energy research, ^[1] generation of high energy particles, ^{[2, 3]} production of X-rays and gamma-rays, ^{[4– 6]} and creation of high energy density conditions comparable to those found in some astrophysical environments.^{[7, 8]} In the 1960s when the concept of inertial confined fusion had just been proposed, laser absorption and plasma heating received immediate attention.^{[9, 10]} Since then, various absorption mechanisms have been proposed. When the laser has a moderate intensity, such as around 10¹³– 10¹⁵ W/cm², the absorption can be dominated by inverse bremsstrahlung or collisional absorption during the laser– solid interaction, ^{[11, 12]} where the laser energy is transferred partially to thermal motion of electrons directly, preferable for the inertial confined fusion. On the other hand, collisionless absorption can play significant roles for laser absorption under different laser and plasma conditions.^{[11, 12]} A well-known mechanism is the so-called resonance absorption, which occurs when the incident laser is p-polarized. In this mechanism, the laser energy is transferred to the excitation of electron plasma waves near the critical density layer where the local electron plasma frequency is equal to the laser frequency. The energy of the electron plasma waves is deposited in plasma via electron acceleration and collisional absorption.

Another well-known mechanism is the development of parametric instabilities, which occur when the plasma density scale length is large.^{[13– 15]} In this mechanism, the laser energy is also partially converted into electron plasma oscillations. The latter leads to the generation of hot electrons up to ∼ 100 keV, which is usually harmful to the realization of inertial confined fusion. The parametric instabilities also directly lead to loss of laser energy by backscattering and side-scattering. Therefore, significant efforts have been made to suppress the parametric instabilities. In recent years, with the construction of high energy lasers at the mega-joule level, such as NIF in LLNL, USA and LMJ in CEA, France, as well as the experimental progress on NIF, studies of the parametric instabilities have received renewed interest.^{[16– 18]}

Another line on the studies of laser absorption is owing to the invention of the chirped pulse amplification (CPA) laser technology and the subsequent development of ultrashort intense lasers since the late 1980s.^[19] It is found that plasma density scale lengths as short as less than a laser wavelength are produced by ultrashort intense lasers, which leads to new features of laser absorption observed in experiments that can be explained by collisional absorption and resonance absorption.^{[20– 22]} This plasma of short density scale lengths is mainly produced by the prepulses before the main pulses. Because of the ultra-small density scale lengths, it provides the opportunity to control the laser absorption by shaping the target surface. For example, it is found both theoretically and experimentally that the sub-wavelength structures at the solid surface can lead to enhanced absorption.^{[23– 27]} Another aspect is that the laser absorption leads to the generation of a large amount of hot electrons.^{[28– 30]} Other new features of laser absorption are associated with the high laser intensity of the ultrashort laser pulses. The laser intensity is related to the laser amplitude by , where λ ₀ is the laser wavelength in μ m, and a₀ is the laser amplitude normalized by m_eω c/e. When the laser intensity approaches 10¹⁸ W/cm², the effect due to relativistic electron motion becomes significant.^[31] The laser pomderomotive force becomes so large that it can accelerate electrons directly. Significant efforts in this topic are associated with a new concept of inertial confined fusion called fast ignition.^{[32– 34]} Because of highly nonlinear features, the problem of laser absorption in the relativistic high intensity regime becomes even more complicated. Often the interaction systems show strong kinetic effects, and large scale numerical simulations with kinetic methods, such as the particle-in-cell (PIC), ^[35] are necessary to understand the involved physics. Generally speaking, the laser absorption depends upon the laser parameters (wavelength, intensity, pulse duration, and polarization) and the target parameters (density distributions, target shapes, materials, and temperature). With the combination of these parameters, there is rich physics involved in the problem of laser absorption.

In this paper, we present an overview of some of the recent progress on laser absorption in laser– solid interactions with ultrashort high intensity laser pulses. Emphasis will be given to the related theory and numerical simulations carried out by our group during the last decade, where the simulations have been performed with our self-encoded PIC code KLAPS developed in the last 15 years.^{[36– 38]}. The outline of the paper is as follows. In Section 2, some nonlinear effects associated with the collisional absorption will be addressed, which occur when the laser has an intensity above 10¹⁵ W/cm², such as the NIF and LMJ lasers. Section 3 is devoted to the problem of vacuum heating usually found in the ultrashort laser– solid interaction, where the plasma density scale length is much less than the laser wavelength. Clusters formed as a special target medium with an intermediate average density can absorb laser energy in a unique way, which will be discussed in Section 4. In Section 5, the effect of sub-wavelength structures on laser absorption will be discussed. In Section 6, we will consider some nonlinear effects associated with the resonance absorption, which include the relativistic effect and the ponderomotive force effect. When the laser intensity is above the relativistic threshold and a large underdense plasma is involved, the laser absorption appears in the form of plasma electron acceleration. In Section 7, a few nonlinear acceleration mechanisms will be discussed briefly, which include laser ponderomotive force acceleration, betatron resonance, and stochastic acceleration. The temperature scaling of electrons heated and/or accelerated by the lasers will be discussed in Section 8. The summary in Section 9 briefly highlights our understanding of this problem.

As the most basic laser energy deposition mechanism, collisional absorption plays an essential role in transferring the laser energy to the plasma. Particularly, it dominates the laser energy deposition in the scenario of inertial confinement fusion (ICF), in which nanosecond laser pulses of intensity I ≤ 10¹⁵ W/cm² interact with the target and deposit their energy into the underdense plasma in the corona region.^[39] By assuming that the scale length of the plasma density is much longer than the wavelength, the collisional absorption coefficient can be solved from the Helmholtz equation^[20]

where ω is the laser frequency, ω _p = (4π n₀e²/m_e)^1/2 is the electron plasma frequency, and ν _ei is the electron– ion collision frequency. For a planar electromagnetic wave propagating in a uniform plasma, we have ∇ · E = 0. In this case, we obtain the following dispersion relation:

Since ν _ei/ω ≤ 1 satisfies well in the underdense region where the collisional absorption happens, we can rewrite the above equation in a Taylor expansion of ν _ei/ω and approximately get

From the above equation, we can see that the collisional absorption will damp the laser pulse and the absorption coefficient K is given by twice the imaginary part of k

Due to the damping by the collisional absorption, the laser intensity I changes during its propagation in a plasma. If the laser pulse propagates in the x direction, the spatial evolution of the intensity I is given by

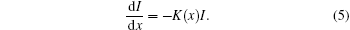As K(x) depends on the electron– ion collision frequency ν _ei, which further depends on the plasma temperature and the Coulomb logarithm lnΛ , it is difficult to analytically solve the intensity evolution from the above equation in general. However, the plasma temperature and the Coulomb logarithm can be assumed to be constant for nanosecond laser pulses at intermediate intensities used in ICF. In this case, K(x) depends only on the density n_e and equation (5) can be solved for given density profiles. By using and ν _ei ∝ n_e, equation (4) can be rewritten as , where ν _ei(n_c) is the electron– ion collision frequency at the critical density n_c.

For a linear density profile n_e = n_c(1+ x/l) in – l ≤ x≤ 0, the absorption rate A = (I_in – I_out)/I_in can be solved from Eq. (5) as^[40]

While for an exponential density profile n_e = n_cexp(x/l) in – ∞ ≤ x ≤ 0, one has^[11]

From the above analysis, one finds that the collisional absorption strongly depends on the electron– ion collision frequency ν _ei. For the usual Maxwellian distribution of electrons, one has

and the Coulomb logarithm lnΛ = ln(b_max/b_min), where the maximum impact parameter b_max is given by the Debye length λ _D and the minimum impact parameter is given by b_min = max(b_⊥ , λ _B), with b_⊥ = Ze²/m_eν ² = Ze²/k_BT_e being the classic impact parameter corresponding to a 90° deflection and λ _B = ħ /m_eν being the de Broglie wavelength according to quantum mechanical considerations. For moderate plasma densities and laser intensities, the Coulomb logarithm varies slowly around 10. However, the more complicated formula for the Coulomb logarithm has to be employed in the laser interaction with denser plasmas.^{[41, 42]}

In the interaction with an intense laser pulse, the electrons may highly depart from the Maxwellian distribution in the equilibrium. Then the precise electron– ion collision frequency should be calculated from kinetic equations such as the Vlasov– Fokker– Planck equation. By assuming that the electron oscillating velocity u₀ in the laser field is much smaller than the electron thermal velocity v_te, Langdon^[43] found that the electron distribution can be approximated by a super-Gaussian distribution and the electron– ion collision frequency may decrease to half of the value estimated by Eq. (8) accordingly. By further increasing the laser intensity, Weng et al. found that the electron distribution approximately becomes an oscillating Maxwellian distribution, and the effective electron– ion collision frequency decreases obviously with increasing laser intensity.^[44] Therefore, the heating rate due to the collisional absorption will decrease with increasing laser intensity in the region I > 10¹⁵ W/cm² as shown in Fig. 1, which is in fairly good agreement with the molecular dynamic simulation results by David et al.^[45] and the experimental results by Ping et al.^[46]

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. The heating rate R due to collisional absorption averaged over the first four laser cycles as a function of the laser intensity obtained from Langdon’ s operator (short dashed line), molecular dynamic simulations by David et al. (dash-dotted line), and Fokker– Planck simulations by Weng et al. (triangle). The plasmas and laser parameters are given as follows: electron density ne = 1020 cm– 3, initial temperature Te = 10 eV, ionization state Zi = 1, and laser wavelength λ = 1.06 μ m.[44]

As shown in the above section, the electron– ion collision frequency obviously decreases with increasing laser intensity in the region I > 10¹⁵ W/cm². Therefore, the energy of an intense laser pulse will deposit into the plasma mainly by collisionless absorption mechanisms rather than the inefficient collisional absorption in this region. The vacuum heating proposed by Brunel for the oblique incidence of a p-polarized laser pulse onto a step-like highly overdense target is one of the most noted collisionless absorption mechanisms.^[47] The efficient absorption of laser energy and the consequent hot electron generation by the vacuum heating have been illuminated by simulations and experiments.^{[48, 49]}

The underlying physics of this mechanism is shown in Fig. 2. If a p-polarized laser pulse irradiates under angle α from the left side onto a step-like highly overdense target with density n_e ≫ n_c, there will be a laser field component perpendicular to the target surface at x = 0

where R is the reflectivity, and E_L is the amplitude of the incident laser field. At the normalized τ _l = ω t_l, the skin depth of the laser field is given by Poisson’ s law

Therefore, the normalized electric field felt by the electrons in the layer at x = x_0l can be expressed as

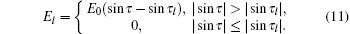From Eq. (10), we can obtain the maximum skin depth as x₀ = ɛ ₀E₀/en₀. Therefore, the areal number density of electrons that interact with the laser field in one laser cycle is given by N₀ = n₀x₀ = ɛ ₀E₀/e. By introducing the normalized velocity w_l = v_l/v₀ with v₀ = eE₀/m_eω , the velocity of electrons from the layer x = x_0l can be solved from Eq. (11) as

The integral of the above equation results in the normalized trajectory s_l = x_lω /v₀,

at time τ > τ _l.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Configuration of Brunel’ s absorption model. A p-polarized laser pulse at intensity IL irradiates onto a highly overdense target under angle α and is partially reflected. At time instant τ l = ω tl, the resulting x component E0(τ l) penetrates up to the position x0l.

From Eq. (13), the orbits of electrons from different layers can be solved numerically. Consequently, the times τ _{l, f} when these electrons return back to the target can be determined. Substituting these return times into Eq. (12), one can obtain the final velocity w_{l, f} at which the electrons enter into the target.^[50] Representative orbits from layers 0 ≤ τ _l ≤ π /2 are shown in Fig. 3(a). It is found that all electrons from these layers are pulled out into the vacuum and later return to the target. Furthermore, it takes a longer time for the electrons from the more superficial layer to return back to the target, and the electrons from some of the most superficial layers can not return back to the target during the first laser period. The velocity w_{l, f} at which the electron returns back to the target is shown as a function of τ _l in Fig. 3(b). We can see that the maximum return velocity reaches w_f = 2.13, high-speed electrons in the neighborhood of this maximum come back late; the electrons from the layers at τ _l < 13° come back only after two periods and their return velocities are highly sensitive to their initial positions.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Time evolution of layer displacements s(τ ), the initial positions of these layers are indicated in degrees on the ordinate at the right; (b) the return velocity wlf as a function of the layer initial position.

Of particular interest is the absorbed energy in a laser period, which is equal to the kinetic energy of fast electrons generated in one period. The latter can be calculated by the following integral:

As shown in the above paragraph, the return velocity w_{l, f} is highly sensitive to the initial position τ _l if τ _l is close to zero. Therefore, it is not possible to rigorously perform the integral (14) from τ _l = 0. Concerning the fact that the electron number at the interval dτ _l is proportional to sin τ _l, we in practice can perform the integral (14) from τ _{l, min} = τ _l(τ _{l, f} = τ _max), i.e., neglecting the electrons whose return times are longer than τ _max. Setting τ _max = 3π , Mulser et al. solved the integral numerically and obtained the absorbed energy in one period^[50]

with η = 1.74. While the incident laser energy in one period is given by

Combining Eqs. (15) and (16), one can obtain the absorption rate A due to the vacuum heating

where a₀ = eE_L/(m_eω c) ∝ I^1/2 is the dimensionless amplitude of the laser electric field, and usually the reflectivity R is equal to 1 – A. From the above formula, we can see that the absorption rate A increases rapidly with the increasing incident angle.

It is important to note that the absorption rate obtained from Eq. (17) will increase almost linearly with the increasing incident laser field amplitude. However, this is not true due to the relativistic effect. Since the electron return velocity in a relativistically intense laser pulse approaches the light speed in a vacuum, the relativistically corrected kinetic energy instead of should be used to calculate the absorption energy by electrons and then result in

Consequently, the absorption rate due to the vacuum heating in a relativistically intense laser pulse is given by

Moreover, we have assumed that the generated fast electrons only move in the normal direction of the target. However, particle-in-cell (PIC) simulations^{[51, 52]} found that fast electrons move roughly along the laser propagation direction. Including the electron kinetic energy due to the motion parallel to the target, Mulser et al. found that the corrected absorption rate can be enhanced approximately by a factor of two.

There are two other related mechanisms of collisionless absorption found with steep density profiles, which occur even under normal incidence of laser light. One is called the sheath inverse bremsstrahlung found when electrons reflect from a sheath potential while oscillating in the laser fields.^{[53, 54]} This mechanism is found for low light intensities. Another mechanism is called J × B heating caused by the 2ω oscillating component of the laser ponderomtive force.^[55] This force generates an electrostatic field in plasma, leading to random electron heating. Usually it requires incident lasers at high intensity. As a comparison, we note that the time averaged ponderomotive force tends to accelerate electrons in the forward direction, which we shall discuss in Section 7.

Owing to their intrinsic properties, clusters are distinct from single atoms and solids in the interaction with intense laser pulses.^{[56– 58]} One of the most obvious phenomena is the efficient absorption of laser energy in clusters due to the strong plasma resonance.^{[59– 64]} Laser– cluster interactions are potentially efficient neutron sources^[65] and ultrashort X-ray sources^[66] owing to the potential efficient laser absorption.

It is convenient to divide the laser– cluster interaction into three stages, namely, atomic ionization, laser– nanoplasma interaction, and ion expansion.^[67] At the first stage during the leading edge of the laser pulse, each atom in the cluster is ionized independently by the laser electric field. Most of the ionized electrons at this stage stay inside the cluster, and they are attracted by the ionized atoms to form a cluster nanoplasma. At the second stage, the strong coupling between the laser pulse and the cluster nanoplasma happens through a few different processes. Among these processes, the plasma resonance is the most important one responsible for the efficient absorption of laser energy in the cluster. At the third stage after the end of the laser pulse, the Coulomb explosion of bare ions occurs if most of the electrons are blown off, or the quasi-neutral hydrodynamic expansion occurs if most of the electrons remain in the cluster.

Usually, the initial eigenfrequency of the cluster nanoplasma is much higher than the laser frequency due to the high initial charge density of ions. However, the ion charge density decreases as the cluster nanoplasma expands in the interaction with the intense laser pulse. Therefore, if the laser pulse is long enough, the cluster eigenfrequency will decrease gradually and accord with the laser frequency at a certain stage. Consequently, the plasma resonance occurs, and the laser energy is absorbed efficiently by the resonantly oscillating electrons.

The plasma resonance in the laser– cluster interaction can be well described by the harmonic oscillator model.^{[61– 63]} In the fluid description of collisionless plasmas, the electron density distribution n_e(r, t) and the velocity distribution υ (r, t) are governed by the continuity and the momentum equations

where 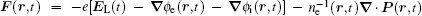is the total force acting on the local electron fluid, with the external laser field E_L(t), the scalar electric potentials of the electrons ∇ ϕ _e(r, t) and the ions ∇ ϕ _i(r, t), and the electron pressure tensor P(r, t). With the simplification that the electron fluid is incompressible, the electron cloud will oscillate in the laser filed without deformation, thus

with x(t) being the center-of-mass coordinate of the electron cloud. Consequently, the electron density, potential, and pressure tensor can be written as functions of only one variable: ξ = |r – x(t)|, i.e., , and P(r, t) = P⁰(ξ ), while . The superscript “ 0” refers to quantities at t = 0. Combining Eqs. (21) and (22), we obtain

Multiplying the above equation by m_en_e(r, t) and then integrating over space, we obtain the equation for the center-of-mass motion of the electrons

where

is the force from the scalar electric potentials with respect to the ions. The contribution with respect to the electron potential ϕ _e(r, t) and the pressure P(r, t) have been neglected in Eq. (24) under the assumption of spherical symmetry. Further, we assume that the displacement amplitude of the electron cloud is much smaller than the cluster radius R(t). In this case, we can rewrite the nonlinear Eq. (24) by a Taylor expansion. Neglecting the nonlinear terms but introducing the damping due to the internal heating, we finally obtain

where is the cluster eigenfrequency, and Q(t) is the total ion charge in the cluster. The phenomenological damping rate Γ (t) is introduced to account for the internal heating of the electrons. Usually, the cluster eigenfrequency Ω (t) and the damping rate Γ (t) vary slowly with time. Then, the solution of Eq. (26) for a linearly polarized laser field E_L(t) = E₀(t)cos(ω t)e_x is given by

with

As Ω (t) and Γ (t) are assumed to be varying slowly, amplitude A(t) and phase Φ (t) are slowly varying functions of time. The energy gain from the laser field averaged over a laser cycle can be calculated as

The above equation indicates that the significant absorption of laser energy happens if Φ (t) = π /2, which is equivalent to the resonant condition Ω = ω in Eq. (29).

The efficient absorption of laser energy by the plasma resonance in clusters has been demonstrated by microscopic molecular dynamics (MD) simulations.^[63] The dynamics of an Xe cluster with 923 atoms in a laser pulse is shown in Fig. 4. Irradiating by an intense laser pulse, the cluster expands as shown in Fig. 4(a) due to the repulsive forces between the ionized ions. During this time, the electrons in the cluster are driven collectively back and forth along the polarization direction of the laser, which is evident from their center-of-mass (CM) velocity v_CM shown in Fig. 4(b). Around t = 30 fs, the amplitude of the cluster oscillation increases obviously. From Fig. 4(c), one finds that at t = 30 fs, the phase shift between the laser field and the cluster oscillation is approximately π /2, i.e., the plasma resonance occurs due to the cluster expansion.

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. Dynamics of Xe923 cluster in a strong laser pulse (λ = 780 nm, I = 9 × 1014 W/cm2, rise and fall time 20 fs, plateau for t = − 80, … , + 80 fs). All quantities are shown as a function of time t: (a) radii R of all cluster shells in units of their initial radii R0, (b) center-of-mass velocity vCM of the electronic cloud inside the cluster volume, (c) phase shift Φ (t) of the collective oscillation in the laser direction with respect to the driving laser. Note that the oscillations are spatially along the linear polarization of the laser, whereas the electron velocity perpendicular to the laser polarization is very small.[63]

Early experiments showed near 100% energy coupling of lasers with targets of sub-wavelength surface structures at laser intensity much lower or near 10¹⁵ W/cm².^{[68– 70]} Our recent experiments collaborating with TIFR in India also demonstrated near 100% light absorption by sub-wavelength grating targets with laser intensity at 10¹⁵ W/cm² and above.^[23] The absorption shows a strong dependence on laser reflected angles and polarizations, indicating the dominant mechanism of the surface plasmon resonance. It is interesting to study whether such phenomena also occur at even higher intensity, which is particularly interesting for many applications, such as the generation of high flux hot electrons for fast ignition of inertial confined fusion, ^{[71, 72]} ion acceleration through target normal sheath acceleration (TNSA), ^{[73, 74]} and compact X-ray sources.^[75]

We have developed an analytical model assuming a rectangular grating structure to study the mechanism of enhanced laser absorption by a grating target.^[24] The absorption relies considerably on the parameters of the grating groove surfaces. For example, it is found that when the grating groove depth h satisfies

with N being an arbitrary integer, the laser absorption is most efficient. While it is most inefficient when

Our relativistic two-dimensional (2D) PIC simulations also confirm the analytical results. Figure 5 shows example simulation results. In this simulation, we take plane laser pulses with wavelength λ ₀ = 800 nm and a duration of 20T₀, which are incident along the + x direction and p-polarized along the y direction. Gold grating targets are assumed to be sharp-edged plasmas with Au^{+ 4} ions and initially distributed within x = 100– 105λ ₀. The lasers reach the target surfaces at 21T₀. In this simulation, the laser absorption for the grating targets with proper parameters reaches 94%, while the corresponding absorption for a polished planar target is only 3%. It is found that a periodic charge separation can be efficiently generated in sub-wavelength grating surfaces. Due to the transverse oscillations of electrons in the grating structures driven by the laser electric fields, intense electrostatic (ES) fields are formed, which result in efficient heating of electrons and the laser energy absorption. Besides, some electrons acted by the ES fields are ejected into the vacuum region ahead of the grating grooves. Thus, the energy absorption by these electrons is much affected by the groove depth or the phase difference between the incident and the reflected lights from the grooves. The dependence of the absorption peaks on the grating size and depth is also derived analytically and verified by PIC simulations, as shown partially in Fig. 5(c), where equations (31) and (32) are verified. The dependence of the laser absorption on the grating parameters becomes weak at high intensity, e.g., I > 10¹⁹ W/cm², due to the destruction of the surface structures by such intense laser pulses.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Spatial distributions of (a) ion density, (b) charge density, (c) Ey, and (d) Ex at time t = 21.25T0, where the normalized laser a0 = 0.5, initial electron density ne = 10nc, and grating parameters (d1, d2, h) = (200, 200, 200) nm. (e) Absorption coefficient as a function of grating grove height h for d1 = d2 = 200 nm, where the four curves are the results for different laser amplitudes and plasma densities.[24]

Such sub-wavelength grating-surface targets can be used to increase the conversion efficiency in laser-driven plasma-based proton acceleration due to the extremely high absorption coefficient of the incident laser energy. Proton accelerations due to the laser– solid target interaction have attracted a lot of interest, ^{[3, 77, 78]} not only because such a novel acceleration concept can provide a much higher acceleration gradient compared to that of the conventional accelerators, but also the produced proton beams have a much shorter pulse duration as well as a much lower transverse emittance. Therefore, such proton beams have various potential applications, such as proton cancer therapy^[76] and proton imaging.^[79] The enhanced laser absorption directly contributes to the proton/ion acceleration^[73] via the TNSA mechanism^[80] and collisionless electrostatic shock acceleration (CESA).^{[81, 82]} Our 2D PIC simulations have demonstrated that such targets can greatly increase the proton conversion efficiency compared to the polished planar target.^[83] There exist optimal grating parameters corresponding to the maximum laser absorption, which optimize the proton conversion efficiency.

Resonance absorption has been well studied since the 1970s.^{[40, 84– 86]} It is caused by the linear mode conversion of obliquely incident p-polarized laser light into an electrostatic electron plasma wave (EPW) at the critical surface of an inhomogeneous plasma.^[11] The absorption efficiency can be expressed as^[86]

where α = 2.644 and q = (2π L/λ ₀)^2/3sin²θ , with L being the plasma density scale length and θ the incident angle. This expression fits very well with the numerical result of Forslund et al.^[85] The maximum absorption can reach about 50% when the incident angle of the laser pulse satisfies

With the development of ultrashort-pulse ultraintense lasers in the 1990s, a new parameter regime of very short scale lengths appears, typically on the order of a laser wave length.^{[87– 90]} Another important effect is associated with the nonlinear excitation of EPWs near the critical surface. Even though the driving laser has an intermediate intensity, the EPWs can be driven to a high amplitude even beyond wavebreaking.^[91] The relativistic effect on the excitation of EPWs was studied first by Drake et al.^[92] However, its effect on the resonance absorption was not fully exploited. To consider this effect, an analytical model was proposed.^[93]

Following the capacitor model^{[11, 84]} and taking into account both the relativistic and the ponderomotive-force nonlinearities, one finds that the driven EPW satisfies

where ɛ = eE/(mω ₀c) is the normalized EPW amplitude, with m being the rest mass of electrons, ω ₀ the driving frequency, ν the collisional damping rate, ȳ the time-averaged relativistic factor for electrons, the slowly varying electron density, v_te the thermal velocity of the electrons, and ɛ _d the (normalized) effective driving field, which depends on the incident laser and the plasma parameters.^{[11, 40, 84]} For short-pulse lasers, the ions do not respond and the electron density is given approximately by , where in the weakly relativistic approximation we have ȳ ≈ 1 + 3|ɛ |²/8.^[94] It is also convenient to assume a linear background density profile, namely, n₀ = n_c(1 + x/L), where is the critical density. When removing the nonlinear terms in Eq. (35), the linear resonance absorption can be obtained.

Equation (35) can be solved analytically for some limiting cases. For example, for weak nonlinearity and weak damping, near the critical layer x = 0, one can obtain from this equation

where ɛ has been renormalized by ɛ _d, τ = ω ₀t/2, ξ = x/L, ν ₀ = ν /ω ₀, and . A similar equation was obtained by Morales and Lee^[95] for describing the interaction of plasma ions and electrons with a long-pulse laser, where the plasma response is governed by the ponderomotive-force driven ion-acoustic waves. In contrast, here the response is governed by the excited EPWs and the nonlinearity is associated with the relativistic electron-mass variation in the latter. That is, the “ capacitor” here involves much smaller time and space scales than those given in Ref. [95]. Based upon Eq. (36), Sheng et al. found that the resonance absorption tends to decrease with an increase in the incident field.^[93]

The above analytical model does not include the laser– plasma interaction. In the case when the incident laser has a relativistic high amplitude, additional effects caused by the laser propagation in the plasma may occur, for example, the relativistic effect caused by the incident laser pulse itself. This effect should enable the pulse to be reflected at a higher density γ ^1/2n_ccos θ than that in the linear case, where γ is the relativistic factor for electrons in the laser field at the reflection layer. When the laser intensity is large enough, there may be γ ^1/2n_ccos θ > n_c. This means that the reflection point is even beyond the critical surface for the linear case. Furthermore, at higher laser intensities, the ponderomotive force of the laser pulse can significantly modify the electron density profile. All these effects can significantly modify the absorption behavior. To address all these effects, PIC simulations have been carried out.^{[96, 97]}

Figure 6 shows the absorption as a function of the laser peak amplitude a₀. When the laser intensity is small (e.g., a₀ = 0.01), the electron plasma wave excitation process is mainly linear and the absorption rate is about 0.5, which agrees with the linear theory of resonance absorption. At moderate laser intensities (e.g., a₀ = 0.2), as shown in Fig. 7(b), the electrostatic field near the critical density forms a shock-like distribution, which is predicted by the analytical model given in Eq. (36). Meanwhile, the corresponding density profile near the critical density region is modified significantly and a sharp density peak is formed, as shown in Fig. 7(b). The absorption rate decreases with increasing a₀ until a₀ ∼ 0.5. This agrees qualitatively with our simple model mentioned above that the relativistic effect associated with the EPW excitation tends to decrease the absorption rate. With the further increase of the laser intensity, the absorption rate changes to increase. This is related to the effect caused by the laser ponderomotive force, which tends to drive new density cavities and peaks around the initial critical surface. As a result, more than one critical surface is formed.^[96] At each critical surface, plasma waves are excited. This results in enhanced laser absorption at high laser intensity, as shown in Fig. 6.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Absorption obtained in PIC simulations with different peak amplitudes a0. The other parameters are L = λ 0 and θ = 21.6° . Equation (34) is satisfied for the maximum absorption rate.[96]

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Snapshots of the electron density ne and the excited electrostatic field Ex for (a) a0 = 0.01, L = λ 0, θ = 21.6° , and (b) a0 = 0.2, L = λ 0, θ = 21.6° . Panels (c) and (d) show the space– time evolution of the electron density with the same parameters given in panels (a) and (b), respectively. The initial electron temperature is Te = 10eV and the laser pulse duration is τ = 20τ 0.[96]

When a large scale underdense plasma presents, the absorption of laser energy by the target often appears in the form of electron acceleration, especially when the incident laser has a relativistic high intensity. Plasma electrons can gain energy from the transverse laser field directly, which is re-directed in the forward direction by the magnetic field. These electrons can also gain energy from the longitudinal electric fields excited during the laser propagation in the plasma. Obviously, the laser absorption depends significantly on how the laser pulse propagates in the plasma. The laser pulse propagation is highly related to the laser and the plasma parameters. When the laser pulse duration is sufficiently short and the intensity is high enough, the laser pulse energy is deposited into the plasma by driving a wakefield or an electron plasma wave. The latter can further accelerate some trapped electrons to high energy.^{[98– 100]} For the electron acceleration by the laser fields, there are several different mechanisms. The ponderomotive force of the laser pulse can accelerate some plasma electrons directly to high energy, ^{[101, 102]} which is usually found when the laser pulse duration is short. When the laser pulse duration is increased, it may experience self-focusing, producing a plasma channel. Electrons inside the channel can be accelerated by the so called betatron resonance acceleration.^[31] In the meanwhile, parametric instabilities such as stimulated Raman scattering (SRS) can develop quickly.^{[103– 105]} In addition to depositing the laser energy into electron plasma waves, the backscattered wave from SRS can drive stochastic electron motion, which may trigger efficient electron acceleration in plasma. In the following, we briefly address the related mechanisms of electron acceleration driven by the laser pulses directly.

7.2. Betatron resonance acceleration

When an intense laser pulse propagates in an underdense plasma, because of the laser self-focusing and the transverse ponderomotive force, some electrons located near the laser axis are pushed aside to form a plasma channel. Inside the plasma channel, a resonant acceleration mechanism works, which is analogous to the inverse free electron laser acceleration. Generally, there are two kinds of quasi-static fields inside the plasma channel, i.e., the radial electric field due to electron density depletion and the azimuthal magnetic field due to the current formed by accelerated electrons along the plasma channel. Under the interaction of these fields, the plasma electrons execute periodic oscillations at the so-called betatron oscillation frequency ω _β .

To estimate this frequency, let us consider a stationary cylindrical plasma channel with trapped electrons having uniform density n_e = fn₀ with 0 < f < 1. Here f is the electron deplete factor, while the ion density is n_i = n₀. The net charge density (1 – f)n₀ creates a radial electric field . These trapped electrons are accelerated close to the speed of light and produce a current − efn₀c, with corresponding magnetic field . Solving the equation of the radial motion of an electron in the channel, , one finds that the betatron frequency can be approximately expressed as^[31]

In the meanwhile, when an electron moves at certain speed v_|| along the plasma channel, it sees a reduced laser frequency ω = ω ₀(1 − v_||/v_ph), where v_ph is the phase velocity of the laser pulse in the plasma channel. As soon as

the resonant energy exchange between the laser and the electrons occurs. When the electrons are located at a proper phase, ^[2] the laser energy can be transferred to the electrons. This mechanism, which is called the direct laser acceleration (DLA) to distinguish it from the laser wakefield acceleration, was demonstrated 15 years ago by numerical simulations^[110] and experiments.^[111] This mechanism produces quasi-thermal energy distributions of electrons with the electron temperature scaling proportional to the square root of the laser intensity. Later, this acceleration was also extended to the case with circularly-polarized laser pulses.^{[112, 113]} Generally, this mechanism requires large preplasma, where a plasma channel can be formed with a sufficient length.

It was found later by our group that the DLA may also be found in the laser– solid interaction with small preplasma, provided that the laser pulse is irradiated on the target with a large incident angle, typically over 60° . Figure 8 illustrates typical electron trajectories from a numerical simulation of such an interaction, where the electrons are accelerated along the target surface.^[114] It is found that quasi-static electric and magnetic fields are produced near the target surface, where the electric field tends to pull electrons towards the target and the magnetic field tends to push electrons outside the target. As a result, some electrons in the preplasma can be confined near the target surface and carry out betatron oscillations while being accelerated along the target surface. This mechanism appears to be responsible for the experimental observation of fast electron emission along the target surface.^{[115, 116]}

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Selected electron trajectories along the target surface obtained from PIC simulation, which are typical for the betatron resonance acceleration. The inset shows the initial target density profile along the normal direction of the target surface.[114]

7.3. Stochastic heating and acceleration

The betatron resonance requires that the accelerated electrons satisfy the betatron resonance condition. Generally, most electrons cannot satisfy this condition or only satisfy this condition for a short period of time. On the other hand, it is found that if there are some random transverse perturbations to electron motion in addition to the laser interaction, the electrons can gain energy from laser pulses efficiently.^[117] In plasma, various random fields can be excited. For example, during the laser propagation in plasma, various waves can be excited via parametric instabilities, which may serve as the random perturbations.

Alternatively, it is found that when electrons experience the interaction of two counter-propagating laser pulses, efficient acceleration of the electrons in plasma or a vacuum can be realized provided that some threshold amplitudes of the lasers are exceeded.^{[118– 120]} The threshold amplitudes are associated with the stochastic motion of the electrons in the colliding laser fields. Generally, the nonlinear motion of a test electron in multi-fields can be described as a time-dependent system with two degrees of freedom or more, which is shown to be nonintegrable. In particular, chaos is found when the so-called resonance layers overlap.^{[121– 123]} The latter provides an estimate of the threshold amplitudes of the driving waves for stochastic motion. In the case with one of the driving lasers at a relativistic high intensity, however, the analytical estimation is not easily obtained. Still a quantitative measure of the threshold of the stochastic motion and the degree of stochasticity for a given Hamiltonian system can be obtained by calculating the Liapunov exponents of the trajectories.^{[118, 122]} For example, it is found that if the forward propagating laser amplitude is a₁ = 3.0 and the initial particle velocity is 0.5c, the stochastic motion can be triggered when the backward propagating laser amplitude is a₂ = 0.1.

Electron acceleration is much more efficient in the case with two counter-propagating laser pulses than that with a single laser pulse. This is illustrated in Fig. 9, which shows that even if the counter-propagating laser pulse has a small amplitude, the electrons are accelerated to a maximum energy much larger than the ponderomotive potential.^{[118, 119]} The electrons are accelerated preferably in the propagation direction of the laser pulse with the relatively higher intensity. In a real situation, it is not necessary to inject a counter-propagating laser pulse into the plasma since it can be produced automatically during the propagation of an intense laser pulse in the plasma through processes such as stimulated Raman backscattering, side scattering, or reflected laser fields from high density regions, as shown in Fig. 9(b). The stimulated Raman backscattering wave is often large enough to trigger the stochastic heating and acceleration as demonstrated by numerical simulations.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (a) Electron energy distributions from 1D PIC simulations of laser interaction with test electrons in a vacuum. (b) Electron energy distributions from 1D PIC simulations, where the plasma slab has thickness L = 50λ 0 and density n = 0.04nc. A semi-infinite laser pulse is incident with a peak amplitude of a1 = 3.0.[119]

In summary, generally, two intersecting laser pulses with any angle (except the zero degree) can result in stochastic motion and efficient electron heating and acceleration.^[119]

Most of the absorbed laser energy converts to the kinetic energy of hot electrons, especially when the laser intensity is high. It is usually assumed that the electrons follow a bi-Maxwellian distribution, i.e., dN_e(E)/dE ∼ exp(− E/T) + exp(− E/T_hot), in which the last term plays a much more important role in the applications despite its small population. However, due to the large and complicated equipment used in the intense laser– plasma interaction experiments, it is difficult to monitor T_hot directly in every experiment. Therefore, it would be convenient if one can estimate T_hot with readily available laser parameters and considerable efforts are devoted to this topic.

It is straightforward that T_hot increases with increasing incident laser intensity. Generally, there is a power scaling with the laser intensity according to experimental and simulation results,

where κ and α are certain constants, which depend on the heating and the acceleration mechanisms. In the 1970s, Forslund et al. summarized several works and gave α = 0.67 for and with CO₂ long pulse lasers; ^[134] Schnü ere et al. gave the scaling from their experiment using relatively high contrast short pulse lasers; ^[135] Beg et al. suggested a scaling law with α = 1/3 according to their experimental measurements; ^[136] Mordovanakis et al. obtained α = 0.64 according to their recent experiment results.^[137] In addition, Malka and Miquel found that α = 1/2 for the electrons ejected along the laser propagation direction, 0.33 for the electrons ejected at 22° to this axis in the forward direction and 135° in the backward direction.^[138] Also with ultrashort intense lasers, Wilks et al. gave a scaling law for the ponderomotive force acceleration, ^[139] where I₁₈ is the laser intensity normalized to 10¹⁸ W/cm². For the betatron resonance acceleration, Pukhov et al. gave the scaling ∼ I^1/2.^[110] Similar scaling with the laser intensity was also found by Sheng et al., ^{[52, 118]} who also had taken into account the effect of laser pulse duration. Qualitatively, the κ factor in Eq. (39) can be considered as a function the laser pulse duration, the laser incident angle, and the plasma density scale length, while α is more related to different absorption mechanisms.

In 2013, Cui et al. performed a series of PIC simulations which cover a large range of laser intensities.^[140] The results reveal that the value of α strongly relates to the dominant absorption mechanism. Figure 10 gives a typical time evolution of the electron energy spectrum after t₀, where t₀ represents the time when the reflect laser pulse just leaves the target surface. Hot electron temperatures under different laser and target parameter sets at t₀ are summarized in Fig. 10(b). As one can see, α equals to 1/2 when the laser intensity is high and the pondermotive acceleration dominates the absorption, which agrees with Wilks’ formula.^[139] The scaling with α = 1/3 occurs at the transitional regime between the resonance absorption (at lower intensities) and the pondermotive acceleration (at higher intensities). Since the resonance absorption requires that the incident angle of the laser pulse matches the preplasma scale length, ^[86] as the incident angle deviates from the optimal angle, the resonance absorption at the low-intensity end gets weaker and the related hot electron temperature is lowered. In the meanwhile, the pondermotive acceleration at the high intensity end is insensitive to the incident angle and thus remains invariant. This interplay results in an increase in the α value, as shown by comparing the dash-dot line and the dot line in Fig. 10(b). Normally, the α value relating to the vacuum heating process is larger than 1. These simulation results well support the experiments listed in the previous paragraph. For a given laser intensity, the hot electron temperature also changes with the incident angle of the laser pulses and the plasma density scale lengths, as shown in Fig. 10(c) for example.

Fig. 10.

Figure Option ViewDownloadNew Window

Fig. 10. (a) Typical energy spectrum evolution after t0, where t0 represents the time when the reflect laser pulse just completely leaves the target surface. The laser is incident at 21.6° with intensity 1.37 × 1018 W/cm2 and the preplasma density scale length is λ 0. (b) Hot electron temperature versus incident laser intensity with different parameters. The dashed, dotted, and dash-dotted lines are power fittings of the corresponding data. (c) Angular dependence of hot electron temperature at incident intensity 1.37 × 1018 W/cm2.[140]

To further understand the underlining physics from a theoretical point of view, several analytical models were developed, aiming to give a universally applicable formula in the whole parameter range. Haines et al. derived a theory based on the conservation of energy and longitudinal momentum of the whole laser– plasma system.^[141] Another approach given by Kluge et al. considered the single electron behavior and then averaged it over the distribution function.^[142] These theories can explain some of the experimental data. However, due to the extremely large variables in real experiments and an insufficiency of experiment data in the wide parameter range, it is difficult to justify the universal validity of these theories.

In summary, an overview on the progress of laser absorption during the interaction of ultrashort intense laser pulses with solid targets is presented. When the incident laser intensity is less than 10¹⁵ W/cm², collisional absorption can play a considerable role in addition to collisionless absorption. With the increase of the incident laser intensity, collisionless absorption tends to become dominant. In the case when the prepulse of the incident is small and the plasma density scale length is very short, collisionless absorption mechanisms such as vacuum heating, resonance absorption, and ponderomotive force acceleration are most significant. Sub-wavelength and nano-scale structures at the solid target surface usually lead to enhanced absorption by driving large electrostatic fields at the surface for electron heating and acceleration. With the increase of the plasma density scale length, significant laser absorption is achieved via electron acceleration during the laser propagation in the plasma by betatron resonance acceleration, stochastic heating and acceleration, and laser ponderomotive force acceleration. Different absorption mechanisms lead to different electron temperature scalings with the laser intensity. Generally, it is found that the hot electron temperature scales proportional to with α depending upon different absorption mechanisms and κ depending upon the laser pulse duration, incident angle, plasma condition, etc. Rich nonlinear physics is involved in the problem of laser absorption under different laser and plasma target parameters, which is still far from being completely understood.