Lattice Boltzmann equations (LBEs) can be derived from the BGK approximation of the Boltzmann equation. In the standard LBM without external forces, the evolution of the particles is described as

where τ is the dimensionless relaxation time. We adopt the D2Q9 model and the equilibrium distribution function is expressed as

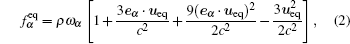where c is the lattice speed, and ω _i is the weight factor equal to ω ₀ = 4/9, ω _{1− 4} = 1/9, and ω _{5− 8} = 1/36 for the D2Q9 model. The equilibrium velocity u_eq is derived from the interacting force, including cohesion force, wall adhesive force, and external force. Using the Shan– Doolen model to incorporate the forcing term, ^{[13, 14]} we have

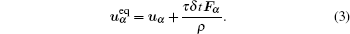The macroscopic density and velocity are expressed as

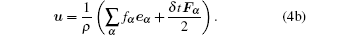The original pseudopotential model was proposed by Shan and Chen.^[1] They approximated the interparticle force by using the nearest neighbor interaction potential, and the force was expressed as

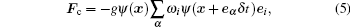where g is the interparticle interaction strength, and the effective mass ψ (ρ ) is formulated as

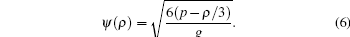The parameter g in Eqs. (5) and (6) is adjusted to ensure that the whole term inside the square root is positive. Similarly, the wall adhesive force takes the form of

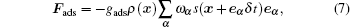where g_ads is the fluid– solid interaction strength. The solid wall is regarded as a phase with constant density s, which is 1 for a solid node and 0 for a fluid node.

To implement Eq. (6), we apply a proper EOS, which describes the relationship between pressure, density (or volume), and temperature for a given substance. In our work, we adopt the CS EOS to acquire larger density ratio and much smaller spurious interface velocity, ^{[6, 8, 15]} which is formulated as

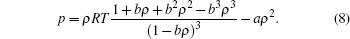To satisfy the critical point conditions, we have

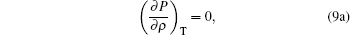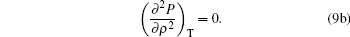By setting T_c = 1, ρ _c = 1, and P_c = 0.01, the parameters are calculated as a = 0.03853462257, b = 0.1304438842, and R = 0.02785855166. In simulation cases of this paper, the reduced temperature is T_r = T/T_c = 0.59. In addition, we introduce a dimensionless coefficient proposed first by Kupershtokh^[8]

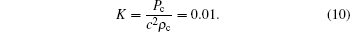Here K represents a crucial factor in the numerical stability of multiphase cases, where smaller K generally results in better numerical stability. Instead of decreasing K by decreasing the δ t/δ x ratio, namely increasing the lattice speed c, we keep a uniform lattice velocity, which is a common practice in most LB simulations and can avoid too many time steps in unsteady problems.

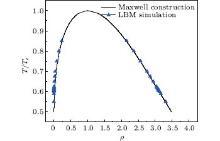
To theoretically predict the density of both liquid phase and gas phase, we solve the Maxwell construction using the integral technique.^[16] The density ratio of up to approximately 160000 (T_c = 0.55) is achieved successfully, and further adjustment of K will lead to an even larger density ratio in our tests. The LBM simulated results fit well with the Maxwell construction in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Coexistence curve of theoretical and calculated density of the CS EOS.

Physically, the surface tension is caused by the attraction between molecules of fluid, and it is an effect within the surface layer of a fluid that causes the layer to behave as an elastic sheet.^[11] The original pseudopotential model does not explicitly contain a surface tension term. Shan and Chen showed that the surface tension term could be exclusively formulated as^[12]

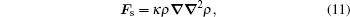where κ determines the strength of surface tension. This scheme offers a flexible choice to adjust the surface tension strength in situations where the surface tension is important.

Numerically, we refer to the finite difference method (FDM) and use the five-point scheme for the calculation of ∇ ²ρ

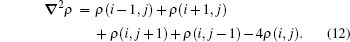The lattice discretized scheme for the gradient term ∇ ∇ ²ρ (assuming ϕ = ∇ ²ρ ) is

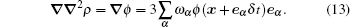By expanding the right term, it can be proved that equation (13) is identical to the six-point method, ^[6] while remaining an easy form to calculate in the lattice evolution loop. By incorporating the surface tension term in the interparticle interaction force, equation (5) is implemented as follows:

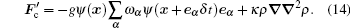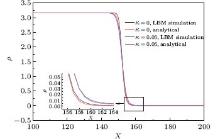
The typical Laplace rule (Fig. 2) indicates that the pressure difference across the drop/bubble interface has an inverse proportional relation to the radius, namely,

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Droplet at T = 0.59Tc. (a) Density distribution; (b) spurious velocity in the x direction.

Figure 2 shows the density and velocity distribution, and we should note that the spurious velocity is unavoidable due to the modeling of multiphase interaction. Besides, the maximum spurious velocity is less than the maximum spurious velocity (namely, 0.092571) using the CS EOS when κ = 0 in Ref. [6]. In Fig. 3, drops/bubbles of various sizes are simulated, and each line satisfies the linear relation well with the slope equal to the surface tension coefficient σ . By changing κ in Eq. (11), we can increase σ by up to 55.4% and decrease σ by about 2% without modifying the initial density ratio.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Plot of curvature (1/R) versus pressure difference.

Another form of surface tension term proposed by Peng is described as F_s = κ ψ (ρ )∇ ∇ ²ψ (ρ ).^[7] However, our simulation results show that the surface tension coefficient increases by 19.2% at most and decreases by 15.0% if the initial density ratio is not modified.

It should be noted here that the interface becomes thicker once the surface tension is strengthened, as shown in Table 1. Since the pseudopotential model is a diffuse-interface method, it is usual that the interface occupies several lattice units. Huang et al. constructed an analytical expression of density distribution of Laplace rule^[14]

Table 1.

Table 1.

Table 1. Properties of droplets (R ≈ 50) for different κ . w denotes the interface thickness. κ | us| max ρ l ρ v σ w – 0.002 0.03582 3.159 0.001021 0.09213 4 0 0.03378 3.159 0.001098 0.09401 4 0.02 0.02071 3.161 0.00195 0.11445 4 0.04 0.01435 3.163 0.002858 0.13185 5 0.06 0.01072 3.165 0.003756 0.14607 5

Table 1. Properties of droplets (R ≈ 50) for different κ . w denotes the interface thickness.

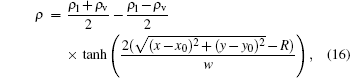where (x₀, y₀) is the center position of domain, and the radius of the droplet is implicitly located, namely, ρ = (ρ _l + ρ _v)/2. Figure 4 shows the coexistence curve in the x direction, and the curve in the range of 0 ≤ x ≤ 100 is just symmetrical to that of 100 ≤ x ≤ 200.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Coexistence curve of LBM simulated and theoretical density distribution in the x direction.

Since the cohesive force in Eq. (5) is the main force that determines the phase interaction, our analysis will concentrate on it. Equation (5) is a discretized form. In fact, there is another equivalent form

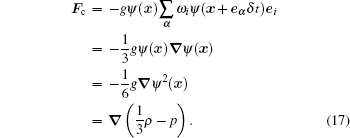In the x direction, we have

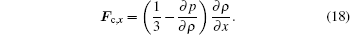In our work, the ratio of critical pressure and critical density is set to be 0.01, ensuring a small ∂ p/∂ ρ ratio. Moreover, a thicker interface means a smaller density gradient (∂ ρ /∂ x) around the interface, making the interaction force smaller. Usually, the density of vapor phase is small and the velocity of vapor phase is easy to vibrate even under small perturbation, which causes the spurious velocity and numerical instability. In our experience, when numerical instability occurs, density changes sharply near the interface, making the interface rather thin. The above analysis can also explain the situation that numerical stability becomes better when κ becomes larger, since the density of vapor phase is larger.

According to Young’ s equation, the contact angle of a droplet on a smooth plate board will satisfy

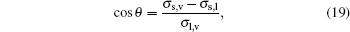where σ _{l, v} is the liquid– vapor interfacial tension, σ _{s, v} and σ _{s, l} are the solid– vapor and solid– liquid interaction strength, respectively. Usually, the contact angle is determined by the solid– liquid interaction strength g_ads only.^[17] By changing κ , we can also acquire different wettability, or hydrophobic/hydrophilic property, on the solid wall, as shown in Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Wall adhesion (the gray arrows denote the velocity vector, with the reference vector of unit magnitude) (a) gads = − 2.0, κ = 0, and θ = 77° ; (b) gads = − 2.0, κ = 0.02, and θ = 114.2.

In our work, although the curve in Fig. 5(b) does not fit linearly as Fig. 5(a), we can also obtain the corresponding relationship before simulating cases involving wall contact angle parameters. Besides, by changing κ , numerical stability is improved.

Cavitation is a catastrophic transition from liquid to vapor, and it is called heterogeneous cavitation when it is nucleated by pre-existing bubbles or other disruptions in the structure of the liquid.^[18] Simulations on heterogeneous cavitation usually concentrated on the critical radius^{[19, 20]} according to the energy theory by Ou and Truller, ^[20] who gave

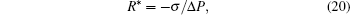where R^* is the critical radius, and Δ P is the outer pressure difference acting on the bubble. If given the pressure difference, a bubble with a radius less than R^* will condensate, while a bubble with a radius larger than R^* will nucleate cavitation. Our simulations deal mainly with different phenomena caused by different surface tension strength. In all cases, the density of the liquid– vapor system is (3.116, 0.08), and the pressure difference is 5.162× 10^{− 3}. To gain different surface tension strengths, the parameter κ in the surface tension term is made 0 and 0.06, individually.

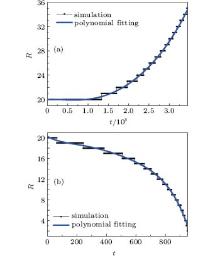
From Figs. 7 and 8, we know that the radius of a bubble changes with time. It should be noted that the radius in every time step is obtained through tracking the interface where the density of the node is closest to 0.5(ρ _l + ρ _v). Thus, only integral data are captured, and the tendency is drawn clearer with polynomial fitting.

Fig. 6.

	Figure Option ViewDownloadNew Window
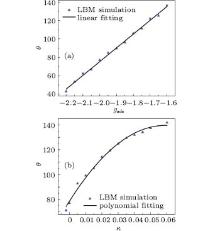	Fig. 6. Coexistence curve of calculated and fitted data of contact angles. (a) κ = 0 and gads varies from − 2.2 to − 1.6. (b) gads = − 2.0 and κ varies from − 0.002 to 0.06.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Effect of surface tension on evolution. (a)– (d) κ = 0, bubble nucleates cavitation. (a) t = 200, (b) t = 2000, (c) t = 3000, (d) t = 3440. (e)– (h) κ = 0.06, bubble dissipates due to condensation. (e) t = 200, (f) t = 500, (g) t = 800, (h) t = 940.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Radius of bubble against time. (a) κ = 0; (b) κ = 0.06.

When the surface tension is strong, more energy for the bubble is needed to expand and it has a tendency to condensate. On the contrary, bubbles will nucleate cavitation. Our simulation results are consistent with the theoretical prediction that the surface tension coefficient lies between 0.09213 and 0.14607 (see Table 1), which corresponds to κ . Thus equation (20) is validated from the prospect of surface tension that the original pseudopotential cannot do.