Corresponding author. E-mail: yhfeng@me.ustb.edu.cn
Project supported by the National Natural Science Foundation of China (Grant No. 51422601), the National Basic Research Program of China (Grant No. 2012CB720404), and the National Key Technology Research and Development Program of China (Grant No. 2013BAJ01B03).
The thermal conductivity of mesoporous material has aroused the great interest of scholars due to its wide applications such as insulation, catalyst, etc. Mesoporous alumina substrate consists of uniformly distributed, unconnected cylindrical pores. Near-field radiative heat transfer cannot be ignored, when the diameters of the pores are less than the characteristic wavelength of thermal radiation. In this paper, near-field radiation across a cylindrical pore is simulated by employing the fluctuation dissipation theorem and Green function. Such factors as the diameter of the pore, and the temperature of the material are further analyzed. The research results show that the radiative heat transfer on a mesoscale is 2∼4 orders higher than on a macroscale. The heat flux and equivalent thermal conductivity of radiation across a cylindrical pore decrease exponentially with pore diameter increasing, while increase with temperature increasing. The calculated equivalent thermal conductivity of radiation is further developed to modify the thermal conductivity of the mesoporous alumina. The combined thermal conductivity of the mesoporous alumina is obtained by using porosity weighted dilute medium and compared with the measurement. The combined thermal conductivity of mesoporous silica decreases gradually with pore diameter increasing, while increases smoothly with temperature increasing, which is in good agreement with the experimental data. The larger the porosity, the more significant the near-field effect is, which cannot be ignored.
Nowadays, research attention have gradually been turned to the nano-scale since micro-electro-mechanical systems (MEMS) developed rapidly. Nano-scale heat transfer including the near-field radiation has been more and more concerned with.[1] Thermal radiation on a nano-scale, i.e., near-field radiation, is different from macroscale thermal radiation, and has size effect.
Early in 1971, Polder and Hove[2] initially deduced the radiative heat flux between two parallel plates with micro-scale gap. Since then, numerous studies on the near-field radiative heat transfer between two semi-infinite bodies, [3– 5] between a spherical particle and a semi-infinite body[6, 7] or between two spherical particles[8– 10] have been carried out.
It has been investigated that as the gap between the two mediums is so small that it is comparable to or shorter than the characteristic wavelength of thermal radiation (λ T), Stefan– Boltzmann law is no longer applicable. The radiation will have wave interference effect and photon tunneling effect, [11– 13] which greatly enhances the radiative heat transfer. The near-field radiative heat transfer can exceed blackbody radiation by 5– 6 orders of magnitude.[14– 16]
Nanoscale radiative heat transfer promotes the research and development of near-field radiation.[17] For a mesoporous material, the near-field radiation across the pore cannot be ignored, which is rarely reported. Although the thermal property of amorphous mesoporous material has caused great attention, [18, 19] the heat transfer mechanism for amorphous mesoporous material is not very clear yet. Therefore, the research of thermal conductivity of amorphous mesoporous material is still a hot point. For amorphous mesoporous alumina film (AAO template) as an amorphous material, its thermal conductivity has been rarely reported relatively.[20, 21]
In this paper, we focus on the near-field radiation across a cylindrical pore by employing the fluctuation dissipation theorem and Green function, and its influence on the thermal conductivity of the mesoporous alumina. Porosity weighted dilute medium (PWDM) model[22] is used to combine the near-field radiation with the thermal conductivities of gas confined in the pore of mesoporous alumina substrate. The combined thermal conductivity of the mesoporous silica is obtained and compared with the measurement. Finally, the effects of the pore size and temperature are also investigated.
Near-field radiative heat transfer across a pore in mesoporous alumina is analyzed. The schematic nanostructure of mesoporous alumina is shown in Fig. 1(a), which consists of uniformly distributed, unconnected cylindrical pores with diameters that can be tailored within a range of 10– 80 nm.[20, 21]
The porosity ϕ is introduced to denote the volume ratio of pores in mesoporous alumina, which is given by 
Since the mesoporous alumina has a periodical structure, a structure element containing a cylindrical pore can be suggested as shown in Fig. 1(b). The pore is characterized by the free-space permittivity ε 0, and bounded by alumina with relative permittivity ε 1. The temperature distribution can be expressed as T(ρ , θ )= 1/2[(T1− T2)ρ cos θ /r + T1 + T2].[23] It drives radiative heat transfer across the pore, where T1 is the high temperature at θ = 0° , T2 is the low temperature at θ = 180° on the pore boundary. As illustrated in Fig. 1(b), heat radiated from a source located at (ρ , θ ) transfers to the point (ρ ′ , θ ′ ) by traveling a distance L= [(ρ 2 + ρ ′ 2− 2ρ ρ ′ cos(θ − θ ′ )]1/2.
 | Fig. 1. (a) Structure of mesoporous alumina. where red spheres represent oxygen atoms, yellow spheres denote aluminium atoms). (b) Simplified a pore for near-field radiation calculation. |
Unlike the far-field radiation (macroscale thermal radiation) transferred by the propagating of the transmissible electromagnetic waves, the near-field radiation is transferred by photon tunneling of the evanescent waves.[24, 25] Now considering a monochromatic electromagnetic wave in the vacuum region, the complex wave vector in a vacuum can be expressed as κ 0 = (β , γ 0), which can be seen in Fig. 2, and κ 0 = ω /c, where c is the speed of light in vacuum, β is the parallel component of the wave vector that is parallel to the plane, γ 0 is the perpendicular component of the wave vector, ω is the angular frequency of the electromagnetic wave.
Assuming that thermal and quantum fluctuations of the current density j inside the body create the fluctuating electromagnetic field, it is known that the time-averaged〈 j 〉 = 0 but 〈 j · j 〉 ≠ 0. We can describe the fluctuating electromagnetic field by the Maxwell equations with the fluctuating current density. According to the electromagnetic wave theory, for a monochromatic wave in a dielectric, isotropic, nonmagnetic body, the Maxwell equations corresponding to radiative heat transfer can be shown as
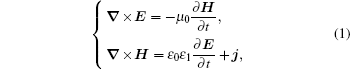 |
where E is the electric field, H the magnetic field, ε 0 the vacuum permittivity, μ 0 the magnetic permeability of vacuum, ε 1 the relative permittivity(dielectric constant) of alumina, and j the fluctuating current density. Considering boundary conditions, the fluctuating electromagnetic field can be obtained, then the frequency-dependent spectral Poynting vector, i.e., spectral heat flow across the pore, is given by
 |
where * denotes the complex conjugate.
Using the fluctuating current density as the source, from the Maxwell equations the electric field can be given by
 |
where κ 1 is the wave vector in alumina, 
When we calculate the radiative heat transfer across a cylindrical pore, the Fourier transform of the three-dimensional expression from z to κ 1Z space is used, and set κ 1Z = 0. The induced electric and magnetic fields caused by the fluctuating current density can be expressed as a frequency-dependent volumetric integral, according to the dyadic Green's function G(ρ , ρ ′ , ω ):
 |
where G(ρ , ρ ′ , ω ) is essentially a spatial transfer function between a fluctuating current source j at a location ρ ′ and the electric field E at another location ρ . The integration is over the region V that contains the source of fluctuating current density.
The radiative heat transfer between the left side and the right side of a curved interface is calculated by employing the dyadic Green’ s function characterizing the electric field, G(ρ , ρ ′ , ω ), which is given as the solution to a inhomogeneous cylindrical Helmholtz equation. The dyadic Green's function must satisfy the boundary condition at the vacuum-silica interface (ρ = r), which can be given by ∇ × G(ρ , ρ ′ , ω ) = iκ 0G(ρ , ρ ′ , ω ). We can obtain the electric Green’ s functions, [23] which can be shown as
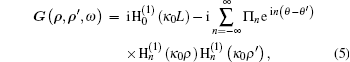 |
where the reflection coefficient can be shown as
 |
where Jn and 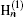

In this paper, the pore diameter in our model is greater than 1 nm since the dielectric function is not local nor dependent on wave vector[15] when the pore diameter is less than 1 nm. Therefore, we can assume that the dielectric function is a scalar (isotropic medium) and independent of the wave vector. The dielectric function can be written as ε 1(ω ), which can be calculated by the data in handbook of optical constants.[26]
The fluctuating current density within the body, as the source, can be described by fluctuation-dissipation theorem (FDT). It is related to the alumina equilibrium temperature T and dielectric function ε 1(ω ). The random thermal fluctuations of charges create a space- and time-dependent fluctuating electric current density 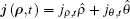
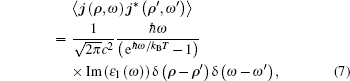 |
where j(ρ , ω ) is the component of fluctuating current density at point ρ , with ω being the angular frequency; δ is the Dirac delta function; 〈 〉 denotes the ensemble averaging, which is an average concept in quantum mechanics.
According to Eqs. (2), (4), (5), and (7), we can obtain the Poynting vector, i.e., radiative heat flow across the pore, which is shown (in units of W· md− 1) as follows:
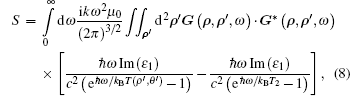 |
where the last term on the right-hand side refers to the net radiative heat flux from 
Finally, equivalent thermal conductivity of radiative heat transfer (in units of W· m− 1· K− 1) can be obtained as follows:
 |
where Δ T = T1− T2.
The combined thermal conductivity of mesoporous alumina is a combination of the thermal conductivity of mesoporous alumina (substrate thermal conductivity), kS, the thermal conductivity of void space (air), kg, and the equivalent thermal conductivity of radiative heat transfer across mesopore, kr.
The thermal conductivity of mesoporous alumina, kS, is lower than that of normal bulk alumina (k0 = 33 W · m− 1· K− 1)[28] since mesoporous alumina is not a crystal but an amorphous material. The kinetic theory is used to calculate the substrate thermal conductivity in the X– Y plane and along the Z direction, and it is shown as follows:[29]
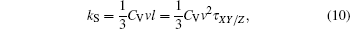 |
where CV is the heat capacity, τ XY/Z is the combined relaxation time, and v is the average sound velocity. So the reduced substrate thermal conductivity scaled by that of the corresponding bulk can be written as
 |
The superscript “ * ” above means a dimensionless quantity scaled by the corresponding quantity of the bulk material. The scaled specific heat capacity of a nanoporous material is a function of the pore radius r and the porosity ϕ , [21]
 |
The values of equation parameters can be obtained from Ref. [20].
The combined phonon relaxation time is obtained from the Matthiessen rule as[30]
 |
On the right-hand side of the above equation, the first term is the reciprocal of the relaxation time corresponding to the scattering in the normal bulk alumina, and l0 is the phonon mean free path of the normal bulk alumina; the second term is the reciprocal of the relaxation time corresponding to the defect scattering, and l1 is a fitting parameter which shows the glass defect levels; in the third term, τ B, XY/Z is the relaxation time corresponding to the boundary scattering. The boundary relaxation rate along the Z direction[31] can be expressed as
 |
The boundary relaxation rate in the X– Y plane can be expressed as
 |
According to Eqs. (11)– (15), we obtain the scaled substrate thermal conductivity as
 |
The substrate thermal conductivity can be written as kS = 2/3ks, xy + 1/3kS, Z.
Zeng et al.’ s model[32] is used to describe the thermal conductivity of confined air in mesopore, kg, as
 |
where the parameter γ = cP/cV, Ng0 = ng/V ϕ , As is the surface area of the shell, Vs the apparent volume of the material, mg the mass of an air molecule, ng the number density of the air molecules, and dg the diameter of an air molecule. An air molecule has a mass of 4.648× 10− 26 kg and a diameter of 3.53× 10− 10 m.[33]
The porosity weighted dilute medium (PWDM) model[22] is used to obtain the combined thermal conductivity of mesoporous alumina by taking into account the thermal conduvtivities of alumina, confined air and near-field radiation. The PWDM model represents thermal conductivity variations of the dilute particle, fluid or other porous materials, through employing a combination of the dilute particle and dilute fluid models, so it is more accurate than the porosity weighted simple medium (PWSM) model, [22] which is a combination of the parallel and serial models. Accordingly, the combined thermal conductivity of mesoporous alumina can be expressed as
 |
where x is the semi-empirical fitting parameter, which ranges from zero to infinity and accounts for the effects of pore shape, pore size, and other parameters; kf = kr+kg.
As is well known, the total radiative heat flux includes the contributions of near-field and far-field electromagnetic waves. For a cylindrical pore surrounded by alumina, T1 = 310 K and T2= 300 K are the temperatures of two sides of the pore, respectively. It can be seen from Fig. 3(a) that the radiative heat flux decreases exponentially with pore diameter increasing. When the diameter is greater than 1nm and less than 100 nm, the contribution of near-field evanescent wave is 2∼ 4 orders of magnitude greater than that of far-field electromagnetic wave. On a nanoscale, the main contribution to the radiation is the evanescent wave of near-field. The smaller the pore diameter, the more significant the near-field effect is. When d is larger than 1000 nm, near-field radiative heat flux is close to far-field radiative heat flux.
 | Fig. 3. Variations of radiative heat flux (a) and equivalent thermal conductivity (b) across a pore with pore diameter (T1= 310 K and T2 = 300 K). |
 | Fig. 4. Variations of radiative heat flux (a) and equivalent thermal conductivity (b) with temperature (pore radius r = 7.5 nm) at T2 = 300 K and Δ T = 10 K. |
Figure 3(b) shows the variation of equivalent thermal conductivity of near-field radiative heat transfer in pores with pore diameter. The equivalent thermal conductivity decreases exponentially with increasing the pore diameter and decreases more rapidly at smaller pore diameter.
The following is concerned with the influence of temperature on the near-field radiation as illustrated in Fig. 4. It is for the case where the pore of radius is 7.5 nm with the temperature T1 ranging from 310 to 350 K. When keeping Δ T = T1− T2 = 10 K, the heat flux of near-field radiation increases smoothly as temperature T1 rises, meanwhile, radiative heat flux is almost increasing linearly when keeping T2 = 300 K with temperature T1 rising. Concerning the equivalent thermal conductivity of near-field radiation, it increases smoothly with temperature T1 going up. It seems that equivalent thermal conductivity under Δ T = 10 K is slightly greater than under T2 = 300 K, since the former mean temperature is greater than the later. Therefore, rising mean temperature can be more significant for raising the equivalent thermal conductivity of near-field radiation than for enhancing the temperature difference.
The porosity and the pore radius of mesoporous alumina films (AAO) can be obtained by the image of scanning electron microscopy (SEM) method, [20] and the results are shown in Table 1.
| Table 1. Structure model and thermal conductivities. |
The hot disk method was used to measure the thermal conductivities of the samples simultaneously in the previous work[20] as shown in Fig. 5. The sensor used in this paper consists of a 10-μ m thick nickel double spiral concentric circle foil, insulated on both sides by a 25.4-μ m thick layers of Kapton polyimide film with good chemical resistance and mechanical properties. This sensor acts both as a heat source for increasing the temperature of the sample and as a resistance thermometer for recording the time-dependent temperature increase of the heat source itself. Exhaustive information about the experiment has already been mentioned in Ref. [20].
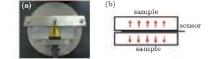 | Fig. 5. Hot disk thermal constant analyzer apparatus. Panel (a) shows hot disk sample holder and sensor, and panel (b) displays sensor and samples. |
We employ the structure models of experiments, which are listed in Table 1. Shell thermal conductivity of mesoporous alumina is denoted by kS, and can be obtained by Eq. (16). The thermal conductivity of air in mesopore is calculated by Eq. (17). Also the equivalent thermal conductivity of near-field radiation across various mesochannels of alumina, kr, can be obtained by Eq. (9). The above calculated data are shown in Table 1.
The combined thermal conductivity of mesoporous alumina with near-field radiation for cylindrical pore considered is calculated from Eq. (18), and the results are shown in Fig. 6(a). The current model is consistent with the measurement. The combined thermal conductivity of mesoporous alumina does not keep decreasing with increasing the porosity since the combined thermal conductivity is determined by porosity and pore radius. The predicted values with considering the near-field radiation are almost 3% higher than those without considering it. This verifies the accuracy of our model.
Meanwhile, the influence of near-field radiation on the combined thermal conductivity of mesoporous alumina is shown in Fig. 6(b). The combined thermal conductivity difference between with and without considering the radiation increases with porosity increasing.
Now we consider the influences of the porosity on the combined thermal conductivity of mesoporous alumina with the temperatures T1= 310 K and T2= 300 K. From Fig. 7(a) it can be found that while keeping the pore radius r = 7.5 nm, the combined thermal conductivity of mesoporous alumina decreases gradually with porosity increasing, since the increase of the proportion of confined air leads to the reduction in the combined thermal conductivity. This result could be attributed to the fact that the air filled in pores has much lower thermal conductivity than the substrate alumina. It should be noted that the pore diameter of actual mesoporous alumina is less than 100 nm, therefore, the near-field radiation across the pore may not be ignored.
 | Fig. 7. Combined thermal conductivities of mesoporous alumina (a) under different porosities and (b) under different mean temperatures respectively. |
The following is concerned with the influence of temperature on the combined thermal conductivity of mesoporous alumina as illustrated in Fig. 7(b), while figure 4(b) shows the equivalent thermal conductivity of near-field radiation changing with mean temperature. It is for the pore radius of 7.5 nm with the temperatures ranging from 310 to 350 K for T1 and from 300 to 340 K for T2, while keeping temperature difference Δ T = 10 K. As the average temperature increases, the combined thermal conductivity of mesoporous alumina increases smoothly, since the increase of the number of phonons and the enhancement of energy transfer can raise the thermal conductivity. The predicted values with considering the near-field radiation are higher than without considering it, so, near-field radiation has an significant influence on thermal conductivity of mesoporous material with small radius.
Near-field radiation has great influence on mesoporous material thermal properties. We focus on the near-field radiative heat transfer across a mesopore and its contribution to the combined thermal conductivity of mesoporous alumina. The main findings and conclusions are summarized as follows.
1) The equivalent thermal conductivities of near-field radiation across a pore under different pore radii and temperatures are investigated. The near-field radiative heat flux on a nanoscale is 2– 4 orders higher than on a macroscale. The equivalent thermal conductivity decreases exponentially with the increase of diameter, and increases smoothly with the rise of temperature, implying that temperature can raise the equivalent thermal conductivity of near-field radiation more significantly. The smaller the pore diameter, the more significant the near-field radiation effect is.
2) The combined thermal conductivity of mesoporous alumina does not keep decreasing with the increase of porosity since the combined thermal conductivity is determined by porosity and pore radius. The predicted values with considering the near-field radiation are almost 3% higher than without considering it.
3) The influence of near-field radiation on the combined thermal conductivity of mesoporous alumina increases with porosity increasing. The combined thermal conductivity of mesoporous alumina decreases gradually with porosity increasing, while increases smoothly with temperature increasing.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|



