As an effective and non-intrusive medical technique proposed in the last century, extracorporeal shock wave lithotripsy (ESWL) is applied worldwide for the treatment of calculi in the human body, such as kidney stones.^[1] This technique has been used to pursue the complete damage of calculi with less side effects. For ESWL, the shock wave acts on calculi and causes extrusion, fatigue, and breaking directly while the cavitation effect caused by negative pressure helps facilitate the breakage of calculi.^[2] Since the original Dornier HM-3 was introduced as a lithotripter in clinical applications in the 1980s, continuous development has been taken on the systems to produce a lithotripter field with optimized peak pressure and beam size.^[1] According to Jian et al., in order to comminute a kidney stone in clinic treatments, the peak pressure at focus was set from 40 MPa to 120 MPa.^[3] Nevertheless, the sizes, depths, and tensile strengths of kidney stones vary in different cases, so a comprehensive understanding of the working mechanisms of ESWL is still necessary. In order to avoid harm to the normal biological tissue, selective action on target is required and the lesions within the focal area need to be controlled precisely by predicting the acoustic field distribution of ESWL transducers.

Although Khokhlov– Zabolotaskaya– Kuznetsov (KZK) equation has been employed to predict the acoustic fields of transducers with numerical approaches, the half aperture angle of the transducer has to be limited within 16.6° to avoid large errors due to parabola approximation.^{[4, 5]} The transducers with wide aperture angles have performed with remarkable superiority in acoustic focusing effect, focusing area, and transmissivity, therefore it is better to use transducers with wide aperture angles in ESWL treatment.

As far as nonlinearity and its influence on waveform distortion are concerned for high-frequency focal systems with wide aperture angles, Tjø tta et al. proposed an equation that can hold for 2^nd Mach number to modeling acoustic propagation in fluids including viscous and thermal losses.^[4] The spheroidal beam equation (SBE) is parabolic, which can precisely predict the propagation of a high-frequency focused beam emitted from a circular aperture.^[6] Considering the nonlinearity, diffraction, and absorption effects, SBE model can effectively predict the distribution of the focusing acoustic field for a transducer with a wide aperture angle.^{[7, 8]} In this paper, the acoustic field distribution of ESWL transducer is analyzed based on the SBE model.

In this section, nonlinear SBE model is used in the ellipsoidal coordinate to illustrate the acoustic beam that propagates in water, the boundary conditions are obtained by equivalent transformation when the source is located at the focus of an ESWL transducer, and the frequency domain algorithm is employed to solve the SBE model on the basis of Fourier expansion.

The ellipsoidal coordinate system (σ , η , φ ) is shown in Fig. 1. In the x– z plane (or the y– z plane), the definition domain of σ is (− ∞ , + ∞ ), the contour curves of its absolute values are ellipsoids; the definition domain of η is [0, 1], its contour curves are hyperbolas with common focuses f₁ and f₂ of interfocal length 2b₀; φ denotes the angle that these contour curves revolve around the z axis with a range of [0, 2π ]. For − ∞ < σ < ∞ , 0 ≤ η ≤ 1, 0 ≤ ϕ < 2π ; , the transformation between ellipsoidal coordinate (σ , η , φ ) and rectangular coordinate (x, y, z) is

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The ellipsoidal coordinate.

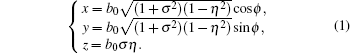For an elliptical transducer, half-angle α ₀ is determined by tan α ₀ = a_f/d_f, where a_f and d_f denote the circular aperture radius and the distance from transducer incision surface to its right focus f₂ respectively. As shown in Fig. 2, the propagation zone can be divided into two parts: the area near the reflecting surface with σ < σ ₀ < 0 and the area near the focal point with σ ₀ ≤ σ . The wave equation for each area is derived by defining an observing point P whose distance to the origin O is.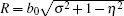

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. A focused ESWL transducer in σ – θ (η ) coordinate plane.

In order to obtain the nonlinear SBE model, the following assumptions are made for simplification: 1) the particles in fluid near source vibrate along the radial direction from the origin; and 2) the acoustic impedance is related to acoustic pressure and particle velocity. Thereafter, the simplified 2^nd-order nonlinear wave equation is then obtained, known as the Westervelt equation^[9]

where p, c₀, and t denote sound pressure, sound velocity, and time respectively; ρ ₀, δ , and β denote density, nonlinear coefficient, and diffusion coefficient of thermal viscous medium respectively.

To ensure the accuracy of calculation of Eq. (2), the aperture angles should be limited to no more than 30° , otherwise, the influence of the nonlinearity on harmonic excitation would become significant and the above simplification of Eq. (2) cannot hold any longer.^[8]

For the area of σ < σ ₀ < 0 where the spherical wave is dominant, by defining delay time t_s = t + R/c₀, the wave propagation is expressed by^[8]

where ɛ = 1/2kb₀, p = p/p₀, and τ _s = ω t_s when k, ω , and p₀ denote the wave number, angular frequency, and the pressure amplitude of the source at the left focus f₁; the angular variable θ is determined by η = cos θ ; is acoustic attenuation coefficient and is the discontinuous distance of plane wave. Since the sound pressure of transducers discussed in this paper is symmetric, the coordinate φ does not appear in Eq. (3).

For the area of σ ≥ σ ₀ and σ ₀< 0 where the planar wave is dominant, the delay time is defined as t_p = t − b₀σ η /c₀. With similar simplification of Eq. (3), in paraxial region, the wave propagation is expressed by^[8]

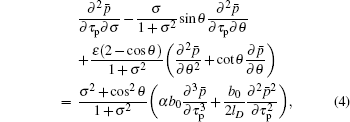where τ _p = ω t_p.

The coupling condition for Eqs. (3) and (4) at σ = σ ₀ is

Equations (3)– (5) are the expressions of nonlinear SBE model, whose solution can be obtained in frequency domain by Fourier series expansion.

For a focused ESWL transducer in σ – θ (η ) coordinate plane, the boundary conditions need to be determined to solve the SBE equations. In Fig. 2, with a, b, and c denoting the semi-major length, semi-minor length, and semi focal of the ellipse, the distance from transducer focus f₂ to its vertex is d= a+ c. As shown in Fig. 3, for σ _max = d/b₀, the source of acoustic wave locates at f₁, the vertex of reflecting surface locates at σ = − σ _max and the focal point f₂ falls at the origin. The surface of σ = − σ _max is not identical to the real surface of transducer reflection.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Equivalent transformation of the source.

In order to focus at f₂, the monochromatic wave radiated from f₁ is equivalent to be radiated from the surface σ = − σ _max. For a spherical wave sourced from f₁, its phase when reaching the surface of the ellipsoid transducer can be expressed as

where is the distance from f₁ to a point P_s on the surface of the transducer.

For the propagation of a spherical wave, the normalized acoustic field distribution of the transducer surface can be obtained as

where d_op = a − c is the distance from transducer vertex to the left focal point.

The sound beams emitting from f₁ focus at f₂ after the reflection of the transducer. Since the transducer surface is rigid, the reflection will cause a phase change of constant π , which does not affect the solution and will be neglected in the following discussion of this paper.

Based on the phase compensation, the phase of P_{σ max}, the equivalent point of P_s on the surface σ = − σ _max, can be expressed as

where is the distance from right focal point f₂ to P_{σ max}, is the distance from right focal point f₂ to P_s. The points P_s, P_{σ max}, and O are collinear.

While equivalently transformed from the transducer surface to the surface of σ = − σ _max, the distribution of acoustic pressure amplitude remains the same; the difference lies in the phase compensating term of kΔ R₀ in Eq. (8).

With the above analysis, after the equivalent transformation between the transducer surface and the surface of σ = − σ _max, the normalized distribution of acoustic field can be expressed as

Since e^{− j2ka} is constant, equation (9) can be further simplified to

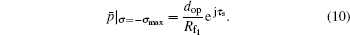The boundary condition for SBE model of an ellipsoid transducer is

where θ ₀ is the angle in ellipsoidal coordinate after the equivalent transformation of half-angle α ₀ to the surface of σ = − σ _max.

For a transducer on ellipsoid (z+ c)²/a²+ x²/b² = 1 in the x– z plane of Fig. 1, according to Eq. (1), the following holds for a point (− d_f, a_f) on the transducer edge

Therefore, the angle θ ₀ can be obtained as

On the other hand, for a point P_s (z, x) on the surface of transducer in the x– z plane, as shown in Fig. 3, with coordinate transformation, the following can be obtained from Eq. (12):

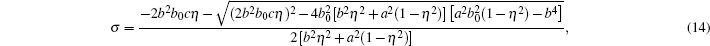with η = cos θ , σ , and η can be obtained by Eq. (14) for a given θ . Consequently, is determined by

The 2^nd-order nonlinear term in the model leads to distortions, thus the distorted waveform can be expanded in Fourier series as^[8]

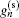
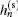
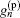
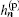
where Fourier expansion coefficients , , , and are the functions of σ and θ , which represent the amplitude components of the fundamental and harmonic waves.

Combining Eqs. (3), (4), and (16), a pair of coupled nonlinear partial differential equations can be obtained. To solve the nonlinear SBE model accurately with the finite difference method, the expansion order should be high enough and the step sizes of σ and θ should be involved. The integration step for θ is taken as 0.2° , the step size for σ is proportionate to 1+ σ ², and σ ₀ = − 1.

The boundary conditions for fundamental wave of both linear and nonlinear SBE models are identical, while the harmonics are zero at the boundary of σ = − σ _max. The relations for fundamental and harmonics at σ = σ ₀ are both determined by

where . Pressure amplitudes for fundamental and harmonics are obtained by taking the square root of the square summation of corresponding Fourier expansion coefficients.

To derive nonlinear SBE model with finite difference method, the following expressions can be obtained by disregarding the superscripts of Fourier expansion coefficients:

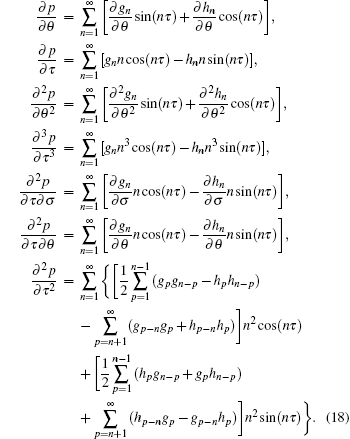Submitting Eq. (18) into Eqs. (3) and (4), the expansions for nonlinear spheroidal beam equations are

where x₃ = σ (1 + σ ²), , E = (σ ² + cos²θ )/(1 + σ ²), and α represents the absorption. The absorption coefficient for an acoustic wave propagating in a medium is

where α _* is the absorption coefficient with the reference frequency f_* .

Combining the differential equations of Eq. (20) with the boundary conditions for fundamental and harmonics, the numerical solution of nonlinear SBE model can be obtained by the finite difference method.

In this section, analyses are carried out for an ESWL transducer of Dornier HM-3 type on its acoustic-field distribution. The length of ellipsoid semi-major axis is a = 14 cm and the length of semi-minor axis is b = 8 cm. Necessary parameters for water are: density ρ ₀ = 1000 kg/m³, acoustic velocity c₀ = 1500 m/s, nonlinear coefficients β = 3.5, μ = 2, acoustic attenuation coefficient of 1 MHz is α _* = 0.0253 Np/m.

3.1. Comparison of linear and nonlinear SBE models

With initial pressure p₀ = 0.5 MPa, source exciting frequency f₀ = 0.5 MHz, transducer half-angle α ₀ = 20° and corresponding σ _max = 2.0, since σ _max = d/b₀, θ ₀ = 17° can be obtained according to Eqs. (12) and (13), θ ₀ is slightly smaller than α ₀.

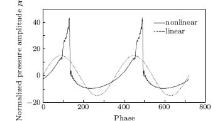
Since the linear SBE model is a particular case of the nonlinear model by setting δ and β as zero, ^[4] the axial pressure distributions for the fundamental wave of linear and nonlinear models are shown in Fig. 4, where ξ = z/d is the normalized axial distance, p_f = p = p/p₀ is the normalized axial pressure, i.e., the pressure gain. The trends of fundamental pressure amplitude for both linear and nonlinear fundamental propagations are alike. However, while approaching the focus, the dashed curve that considers nonlinearity and absorption exhibits a significant deduction with respect to the linear case. At the focal point, the focusing gain of linear and nonlinear propagations are 15.0 and 13.2 respectively. This deduction is caused by not only the energy loss of acoustic absorption but also the energy transduction of nonlinearity, which transfers the energy from fundamental to harmonics. Meanwhile, for both linear and nonlinear models, the oscillations before the focal point are severe while the oscillations after the focal point are relatively steady.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Axial pressure distributions for the fundamental wave of linear and nonlinear models.

Figure 5 shows the axial pressure distributions of the fundamental and the harmonic waves. It can be noticed that the focal gain of the 2^nd and 3^rd harmonics at the focal point are about 50% and 34% of the fundamental respectively. In addition to the satisfying focal gain, the focal areas of the harmonics are smaller and there are no oscillations beside the focus, therefore, the resolution of lithotripsy positioning can be improved and the biological tissue around the calculi will not be harmed when the harmonics are used for treatment. In practice, the harmonics can be extracted for optimized lithotripsy with the fundamental wave filtered out. Although the energy of fundamental is lost, the effect of treatment and the safety of patients can be ensured. Besides, figure 5 also indicates that the focal point is moving to the right with regard to the increase of the harmonic order.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Axial pressure distributions of the 1st, 2nd, and 3rd harmonics.

Figure 6 is the pressure waveform at the focal point f₂ for the linear and nonlinear models, which implies that the time domain waveform of linear propagation remains sinusoidal while the waveform of nonlinear propagation distorts severely, since the principles of lithotripsy are the fatigue crack of calculi caused by forces and the cavitation effect caused by negative pressure during nonlinear propagation. In Fig. 6, during nonlinear propagation, the pressure at focal point increases quickly to a maximal value, which can lead to a stronger pressure impact on the calculi more than the slow action in linear propagation; the pressure falls to negative rapidly after the maximal value, this instantaneous drop of pressure causes remarkable damage to the calculi. Meanwhile, the negative pressure zone of nonlinear propagation is wider and smoother than that of the linear propagation, which indicates that the nonlinear cavitation effect acts on the target longer and cracking the stone can be promoted. In fact, the effect of acoustic nonlinearity on the focused beam is notable in lithotripsy applications. The existence of shock fronts induced by nonlinearity has been experimentally confirmed in real media.^[10] Therefore, the involvement of nonlinearity is essential for the precise prediction of the ESWL acoustic field.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Pressure waveform at focal point f2 for linear and nonlinear models.

3.2. Influence of half-angle α ₀

With initial pressure p₀= 0.5 MPa, source exciting frequency f₀= 0.5 MHz, transducer half-angle α ₀ are taken 10° , 20° , and 30° . Corresponding σ _max and θ ₀ are listed in Table 1.

Table 1.

Table 1.

Table 1. Values of σ max and θ 0 with respect to α 0. α 0 σ max θ 0 10° 2.0 8.8 20° 2.0 16.9° 30° 10.0/3.0 27.3°

Table 1. Values of σ max and θ 0 with respect to α 0.

The axial pressure distributions for the fundamental wave with different α ₀ are shown in Fig. 7. According to the results, the focal point of the fundamental is moving to the right while α ₀ is increasing. Meanwhile, the reflecting surface is enlarged with the increase of α ₀, which leads to the growth of reflected energy and the focal gain at focus.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Axial pressure distributions for the fundamental wave with different α 0.

In order to reveal the influence of half-angle α ₀ on the energy transfer of harmonics, the axial pressure distributions of 1^st, 2^nd, and 3^rd harmonics with α ₀ = 10° , 20° , and 30° are shown in Fig. 8. The maximum pressure gains of 2^nd and 3^rd harmonics are 45.6% and 29% of the fundamental when α ₀ = 10° . For α ₀ = 20° and 30° , the ratios are relatively stable at about 50% and 33.4% respectively. In addition, with the growth of α ₀, the focusing areas are narrowed down, which is essential to avoid the damage of biological tissue nearby. Hence, the half-angle of ESWL transducer should be chosen relatively large in practice.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Axial pressure distributions of 1st, 2nd, and 3rd harmonics with α 0 = 10° (a), 20° (b), and 30° (c).

With different values of α ₀, the pressure waveform at the focal point f₂ are shown in Fig. 9. Both the impact caused by positive pressure and cavitation effect caused by negative pressure are enhanced with the growth of α ₀, which can be used to facilitate the treatment of lithotripsy. Since tan α ₀ = a_f/d_f, for α ₀ = 10° , 20° , and 30° , corresponding aperture radius is 2.4 cm, 5.0 cm, and 7.9 cm respectively when d_f remains the same. Therefore, the transducer geometric parameter can be optimized in order to obtain satisfactory treatment.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Pressure waveform at the focal point f2 with different α 0.

3.3. Influence of fundamental frequency f₀

With initial pressure p₀ = 0.5 MPa, transducer half-angle α ₀ = 20° , and corresponding σ _max and θ ₀ as listed in Table 1, the fundamental frequencies f₀ are taken as 0.25 MHz, 0.5 MHz, and 1 MHz.

The axial pressure distributions of fundamentals with different f₀ are shown in Fig. 10. It can be noticed that while the frequency f₀ increases, the focal point of fundamental is moving to the right and its focal gain grows.

Fig. 10.

	Figure Option ViewDownloadNew Window
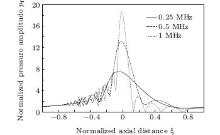	Fig. 10. Axial pressure distributions of fundamentals with different f0.

The axial pressure distributions of 1^st, 2^nd, and 3^rd harmonics with f₀ = 0.25 MHz, 0.5 MHz, and 1 MHz are presented in Fig. 11. The ratios of maximum pressure gains between 2^nd, 3^rd harmonics and the fundamental are 26.6% and 10.41% when f₀ = 0.25 MHz. The ratios become 51% and 34.4% for f₀ = 0.5 MHz, and 72.7% and 69.5% for f₀ = 1 MHz. Therefore, with the increase of fundamental frequency f₀, the ratio of maximum pressure gain between the harmonics and the fundamental grows, which illustrates that a higher fundamental frequency can improve the efficiency of harmonics. Besides, the focal area is narrowed down with the increase of fundamental frequency.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Axial pressure distributions of 1st, 2nd, and 3rd harmonics with f0 = 0.25 MHz (a), 0.5 MHz (b), and 1 MHz (c).

In Fig. 12, the time domain distributions of pressure at the focal point with f₀= 0.25 MHz and 0.5 MHz are presented. Obviously, both the impacts caused by positive pressure and cavitation effect caused by negative pressure are enhanced with the growth of f₀, which can be used to facilitate the treatment of lithotripsy.

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. Pressure waveform at the focal point f2 with different fundamental frequencies.

3.4. Influence of initial pressure p₀

With fundamental frequency f₀= 0.5 MPa, transducer half-angle α ₀= 30° , and corresponding σ _max, and θ ₀ listed in Table 1, the initial pressures p₀ are taken as 0.25 MPa, and 0.5 MPa, corresponding axial pressure distributions of fundamentals, 2^nd and 3^rd harmonics are presented in Fig. 13. With the increase of p₀, although the focal gain of the fundamental decreases, the focal gains of harmonics grow and the growth rate of the 3^rd harmonic is larger, which indicates that the increase of initial pressure p₀ helps the energy to transfer to harmonics. This trend also agrees with the experimental results that increasing p₀ leads to the amplification of the nonlinearity effect with creation of the higher harmonics.^[10] Moreover, the previous experiment has approved that, with increasing the pressure amplitude, the effective energy of lithotripsy can be enhanced and the degree of disintegration can be significantly improved.^[11] In real treatment, the initial pressure p₀ is taken as a relatively large value so that the efficiency of harmonics is improved while the damage of sidelobes to the biological tissue around the calculi is reduced. Even though the decline of focal gain is induced, with the increase of p₀, sufficient energy will concentrate at the calculi for lithotripsy.

Fig. 13.

	Figure Option ViewDownloadNew Window
	Fig. 13. Axial pressure distributions of the (a) fundamental, (b) 2nd harmonic, and (c) 3rd harmonic with different p0.