Quantum coherence and interference can lead to some interesting phenomena such as electromagnetically induced transparency (EIT), ^{[1, 2]} lasing without inversion (LWI), ^[3] giant Kerr nonlinearity, ^[4] four-wave mixing (FWM), ^{[5, 7]} optical bistability and multistability, ^{[8, 15]} superluminal and subluminal light propagation, ^[16] large refractive index, ^[17] atom localization, ^{[18, 22]} and many other novel phenomena.^{[23, 30]} It is known that the dispersion properties of an optical medium can be changed using EIT and quantum interference.^[31] For positive (negative) derivative of refractive index with respect to frequency, the medium displays normal (anomalous) dispersion and the group velocity of the light pulse can be much smaller (greater or even negative) than light speed in a vacuum. These phenomena are called slow (fast) or subluminal (superluminal) light. In recent years, there have been many experimental and theoretical studies of both slow light and superluminal light propagation in quantum systems. Subluminal light propagation has potential applications in optical buffering, data synchronization, optical memories, and optical signal processing. In addition, superluminal group velocities have possible applications in the developing quantum computers, high-speed optical switches and communication systems.^[32] Kim et al. reported experiments in which by the electromagnetically induced absorption (EIA), the superluminal and subluminal light propagation can be obtained in Cs vapor.^[33] The coherent control of dispersion and group velocity has also been shown in Ref. [34] and references therein. These phenomena are reported by adding a fourth level to a three-level EIT system.^[35] It is also shown theoretically that switching between subluminal and superluminal pulse propagation can be obtained by the intensity of coupling field, ^[36] relative phase between applied fields, ^[37] intensity of the incoherent pump, ^[38] and quantum interference from spontaneous emission.^[39] The effects of incoherent pumping field on probe response and dispersion in a Λ -type system in the presence of spontaneously generated coherence (SGC) were also discussed.^[40] It was shown that when the incoherent pump is present the probe response and the dispersion around the resonance depend on the choice of the SGC parameter and phase difference. It was also found that the response of the system changes from EIT to EIA or from EIA to EIT as the values of the SGC parameter and phase difference were properly chosen in the presence of the incoherent pump rate. In another important study, Luo et al.^[41] showed that by RF driving field slow and fast light can simultaneously occur at two frequencies in a Λ -type atomic system. All of the above proposals on subluminal and superluminal light propagation have already been observed in atomic systems. However, for the next generation of all-optical systems, light propagation in a solid state material such as semiconductors and crystals is important to analyze. Subluminal and superluminal propagation of an electromagnetic field in a solid state medium have been studied by many research groups in recent years.^{[42, 44]} For example, Jafari et al.^[42] investigated the propagation of an electromagnetic pulse through a dielectric slab doped with a three-level ladder-type atomic system. It was shown that group velocities of the reflected and transmitted pulses can be switched from subluminal to superluminal light propagation by changing the thickness of the slab or intensity of the coupling field. In our recent study, ^[43] we showed that the reflected and transmitted pulses can be tuned from subluminal to superluminal at different wavelengths by changing the spin coherence in the defect dielectric medium. Moreover, the effects of quantum interference and quantum coherence on the pulse propagation in a semiconductor's medium have also been discussed by many research teams, such as all-optical switching, ^[45] optical bistability and multistability, ^{[46, 58]} Kerr nonlinearity, ^{[59, 60]} etc.^{[61, 65]} In addition, solid crystals such as Er³⁺-doped yttrium aluminum garnet (YAG) crystal is an efficient active medium for lasers operating in the middle infrared band, coinciding with the telecommunications band. Quantum interference and quantum coherence phenomena such as EIT, ^[66] large refractive index without absorption, ^[67]lasing without inversion, ^[68] giant Kerr nonlinearity, ^[69] and optical bistability^{[70, 71]} have also been studied in rare-earth-doped crystals. However, these studies in Er³⁺: YAG crystal were all done under the same concentration of doped ions. The purpose of our paper is to examine the effects of Er³⁺ ion concentration on subluminal and superluminal light propagation in Er³⁺: YAG crystal. In the rare-earth doped crystal, the decay rate of population and electric dipole moment are changed by the concentration of the doped ion.^[72] To the best of our knowledge, no more theoretical and experimental studies on subluminal and superluminal light propagation have been carried out to explore the effects of Er³⁺ concentration and incoherent pump in Er³⁺-doped YAG crystal. We find that the Er³⁺ ion concentration and incoherent pumping field can influence the absorption– dispersion process and group index of weak probe field. Moreover, our results show that Er³⁺ ion concentration has a major role in lasing without inversion and absorption with inversion. Furthermore, our study is much more useful than its gaseous counterpart due to its flexible design and the wide modifiable parameters.

Consider a four-level Er³⁺ ionic system in an Er³⁺-doped YAG crystal as shown in Fig.  1. The energy-level scheme is relevant to the Er³⁺ ions in Er³⁺: YAG crystal, where levels |1⟩ , |2⟩ , |3⟩ , and |4⟩ correspond to energy levels of Er³⁺ ions ⁴I_15/2, ⁴I_13/2, ⁴I_11/2, and ⁴I_9/2, respectively. The detailed level structure and the corresponding transition wavelength can be found in Ref. [73]. In this scheme, a strong coupling field with Rabi-frequency Ω _c drives the |1⟩ ↔ |3⟩ transition. A weak probe field with Rabi-frequency Ω _p couples the |1⟩ → |4⟩ transition. An incoherent pumping field with pumping rate r is exerted between levels |2⟩ and |4⟩ . With the usual phenomenological addition of incoherent pumping and relaxation processes, the elements of density matrix equations can be calculated. Thus, in the rotating wave approximation, the density matrix equations of motion for this system can be obtained as

where

Here, γ _ij are the spontaneous decay rate and represent the coherence relaxation. The detuning parameters are defined as Δ _c = ω ₃₁ − ν _c, Δ _p = ω ₄₁ − ν _p, where ω _ij are the frequency difference of level |i⟩ and |j⟩ , and ν _p (ν _c) is the frequency of probe (coupling) field. The Rabi frequencies are defined as

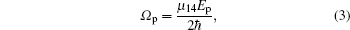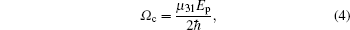where μ _ij is the electric dipole moment between level i and level j of Er³⁺ ion, and given by^{[74, 75]}

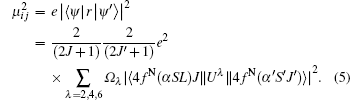Here, the eigenvector ψ may be expressed as a linear combination of the unperturbed states corresponding to an arbitrary coupling scheme; ^[75]Ω _λ is the phenomenological intensity parameter; Jand J′ are the quantum numbers of angular momentum of the levels |i⟩ and |j⟩ respectively. The factor 2 in Eq.  (5) arises from the Kramers degenerate of the Stark levels of Er³⁺ ion. The squared reduced matrix elements |⟨ 4f^N(α SL)J||U^λ ||4f^N(α 'S'J')⟩ |² can be obtained from Ref. [76] and the spectral intensity parameters can be described by an empirical formula^[72]

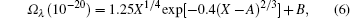where X is the concentration of doped ions; A and B are empirical parameters, i.e., A = 1.0 and B = 0.33 for Ω ₂ , A = 1.1 and B = 0.72 for Ω ₄, and A = 1.4 and B = 0.59 for Ω ₆. From Eqs.  (4)– (6), it can be seen that the concentration of doped ions greatly affects Ω _λ . Moreover, it produces a dramatic influence on μ _ij.^[72] Based on the experimental results, ^[72] the spectral intensity parameters for the five Er:YAG crystals containing Er³⁺ ion concentrations of 29.06, 20.57, 17.38, 0.79, and 0.52 at.% are calculated and listed in Table  1. The values of population spontaneous emission probability Γ _ij of the Er³⁺: YAG crystals and electrical dipole moments under different concentration are listed in Table  2.^[72]

Fig.  1.

	Figure Option ViewDownloadNew Window
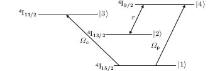	Fig.  1. Er3+:YAG crystal interacting with two laser fields and an incoherent field. Probe field couples |1⟩ ↔ | 4⟩ transition, and control field drives |1⟩ ↔ |3⟩ transition. An incoherent pump field with the pumping rate r acts on |2⟩ ↔ |4⟩ transition.[68]

Table 1.

Table 1.

Table 1. Spectral intensity parameters of Er3+:YAG crystals containing different concentrations of the Er3+ ion at room temperature[72] Concentration of Er3+ ion Spectral intensity parameters/10− 20 cm2 crystal/at.% Ω 2 Ω 4 Ω 6 0.52 1.16 1.52 1.33 0.79 1.35 1.70 1.47 17.38 0.52 0.92 0.79 20.57 0.47 0.87 0.74 29.06 0.40 0.79 0.66

Table 1. Spectral intensity parameters of Er3+:YAG crystals containing different concentrations of the Er3+ ion at room temperature[72]

Table 2.

Table 2.

Table 2. Radiative transition probabilities and electric dipole momenta of Er3+:YAG crystals containing different concentrations of Er3+ ion.[72] Concentration of Er3+ ion crystal Transition probabilities/s− 1 μ 14/10− 32C· m Γ 21 Γ 32 Γ 31 Γ 43 Γ 42 Γ 41 0.52 239.1 38.4 190.6 10.3 68.3 206.5 2.490 0.79 258.8 41.1 216.4 16.3 76.6 211 2.618 17.38 184.6 29.8 128.7 7.6 46.7 127.4 1.920 20.57 187.8 31.2 129.4 7.9 48 152.4 1.858 29.06 175.4 29.3 122.3 7.6 44.6 85 1.755

Table 2. Radiative transition probabilities and electric dipole momenta of Er3+:YAG crystals containing different concentrations of Er3+ ion.[72]

Here, we can estimate the dephasing decay rate as according to Refs. [77] and [78]. Equations  (1) and (2) can be solved numerically to obtain the transient and steady state response of the medium. In fact, response of the medium to the applied field is determined by the linear susceptibility χ , which is defined as

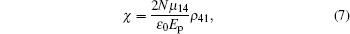where N is the number of doped ions per unit volume and is proportional to concentration of Er³⁺ ions; χ ′ (χ ″ ) is the real (imaginary) part of susceptibility χ which is defined as χ = χ ′ +iχ ″ . The gain or the absorption coefficient for probe field is proportional to the imaginary part of susceptibility χ , i.e., χ ″ . If χ ″ > 0 (χ ″ < 0), the probe laser will be absorbed (amplified). For further discussion, the group index n_g = c/v_g is introduced, where c is the speed of light in the vacuum and the group velocity v_g is given by^{[79, 80]}

Thus, the group index of the probe field is given by

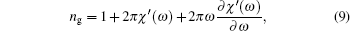where χ ′ (ω ) is the real part of the susceptibility.

The absorption, dispersion and group index are governed by Eqs.  (7) and (9). It is known that imaginary and real parts of susceptibility depend on dipole moment, detuning, incoherent pumping field, coherence relaxation rate, and Rabi frequency. According to Eq.  (5), dipole moment and coherence relaxation rate can be changed with concentration of doped ions. Therefore, the coherent and incoherent fields and concentration of doped ions can greatly affect the absorption, dispersion and group index of weak probe field. In the following and in the presence and absence of incoherent pumping field, the effects of concentration of doped ions and coherent coupling field on absorption, dispersion and group index are discussed, respectively. For normal dispersion ∂ χ ′ (ω )/∂ ω > 0, the group velocity is smaller than the phase velocity, while for anomalous dispersion ∂ χ ′ (ω )/∂ ω < 0, the group velocity can be larger than the phase velocity, or even becomes negative.^{[39, 81, 82]} Recently, numerous studies of subluminal and superluminal light have been reported, ^{[83, 85]} and practical device applications are suggested in optical processing and quantum manipulations, such as optical buffer, switching and storage devices.^{[86, 90]}

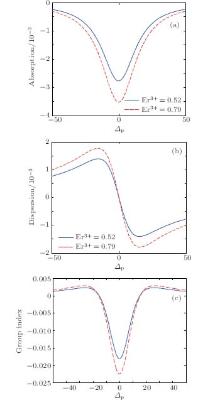
In the following, numerical results are presented. The properties of absorption (Fig.  2(a)), dispersion (Fig.  2(b)), and group index (Fig.  2(c)) of the probe field versus the probe detuning in the absence of incoherent pumping for different values of the Er³⁺ ion concentration are displayed in Fig.  2. It is realized that for every value of the Er³⁺ ion concentration, the probe amplification occurs and the slope of dispersion is negative, corresponding to the superluminal light propagation. The plots of corresponding group index versus probe field detuning are also displayed in Fig.  2(c). They are in good agreement with the plots in Fig.  2(b). Here, the anomalous dispersion appears in the spectral range ∆ _p ≈ 0, especially when Er³⁺ ion concentration equals 0.79%, the slope gradient ∂ χ ′ (ω )/∂ ω of the dispersion curve is greatest. Considering the definition of the group velocity, it is seen that a superluminal group velocity is achieved. Moreover, the amplification for 0.79% Er³⁺ ion concentration is greater than those obtained under other concentrations. Therefore, it is found that by properly adjusting the Er³⁺ ion concentration, the present system provides a high refractive index by probe amplification and superluminal light propagation. Thus, one can see that the high index of refraction without absorption evidently varies with the Er³⁺ ion concentration, but the maximum value is obtained for a value close to the 0.79% Er³⁺ ion concentration. In the presence of the incoherent pumping field, the calculation results are shown in Fig.  3, which shows that the amplification and dispersion change dramatically with Er³⁺ ion concentration. According to the previous results, the maximum values of refractive index in the presence of incoherent pumping field are 0.52 and 0.79 at.% Er³⁺ ion concentration. The effects of Er³⁺ ions for concentration 17.38% (solid line) and 29.06% (dashed line) on absorption (Fig.  4(a)), dispersion (Fig.  4(b)), and group index (Fig.  4(c)) are displayed in Fig.  4. It can be seen that the slope of dispersion changes to positive and probe amplification is converted into probe absorption. Thus, the subluminal light propagation with probe absorption is obtained. In Fig.  5, the absorption (Fig.  5(a)), dispersion (Fig.  5(d)), and population inversion (Fig.  5(c)) are plotted with respect to the coupling field Ω _c for different values of Er³⁺ ion concentration. It can be seen that the amplification by enhancing the Rabi frequency of coupling field changes to absorption and the refractive index increases simultaneously. It is observed that the magnitudes of refractive index and probe absorption (amplification) change with Er³⁺ ion concentration. It can be seen that the magnitude of high refractive index for negative absorption is larger when the value of Er³⁺ ion concentration is smaller. When Er³⁺ ion concentration equals 29.06%, the magnitude of the refractive index is maximum, but the probe absorption has a maximum value. The behaviors of population inversion versus Rabi frequency of coupling field for different values of Er³⁺ ion concentration are also shown in Fig.  5(c). It is found that for Ω _c ≃ 4, the population inversion does not occur for 0.52% and 0.79% Er³⁺ ion concentration, but it does occur for 17.38% and 29.0% Er³⁺ ion concentration. Therefore, it can be found that for 0.52% and 0.79% Er³⁺ ion concentration, the lasing is obtained in the absence of population inversion, and for 17.38% and 29.0% Er³⁺ ion concentration, the absorption is obtained in the presence of population inversion.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Absorption, (b) dispersion, and (c) group index of probe response versus detuning ∆ p for different Er3+ ion concentrations in the absence of incoherent pumping field. The selected parameters are Ω p = 0.1, Ω c = 3, and ∆ c = 0.0.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Plots of (a) absorption, (b) dispersion, and (c) group index of probe response versus detuning ∆ p for 0.52% (solid line) and 0.79% (dashed line) of Er3+ ion concentration. The selected parameters are Ω p = 0.1, Ω c = 3, ∆ c = 0.0, and r = 1.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Plots of (a) absorption, (b) dispersion and (c) group index of probe response versus detuning ∆ p for 17.38% (solid line) and 29.06% (dashed line) of Er3+ ion concentration. The selected parameters are Ω p = 0.1, Ω c = 3, ∆ c = 0.0, and r = 1.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Plots of (a) absorption, (b) dispersion and (c) population inversion versus Rabi frequency Ω c for different values of Er3+ ion concentration in the presence of incoherent pumping field. The selected parameters are the same as those in Fig.  2.

In this paper, we theoretically study the absorption– dispersion process and group index properties of weak probe field in an Er³⁺:YAG crystal. It is found that Er³⁺ ion concentration and incoherent pumping field can affect the propagation of weak probe light in a medium, which can be used for manipulating the sub-super luminal light propagation without absorption in the medium.