Corresponding author. E-mail: jswang@qfnu.edu.cn
Corresponding author. E-mail: fhym@ustc.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 11147009, 11347026, and 11244005), the Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2013AM012 and ZR2012AM004), and the Natural Science Foundation of Liaocheng University, China.
By extending the usual Weyl transformation to the s-parameterized Weyl transformation with s being a real parameter, we obtain the s-parameterized quantization scheme which includes P– Q quantization, Q– P quantization, and Weyl ordering as its three special cases. Some operator identities can be derived directly by virtue of the s-parameterized quantization scheme.
The Weyl transformation[1] of a classical function h(p, q) is defined as
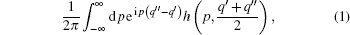 |
which is useful in quantum statistics and path integral.[2, 4] When h(p, q) is quantized as the operator function H(P, Q) through the Weyl correspondence
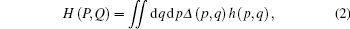 |
where Δ (p, q) is the Wigner operator in the coordinate eigen-vector | q⟩ representation[3]
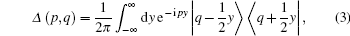 |
then the matrix element of H is just the Weyl transformation
 |
which has been used in the mid-point path integral theory.[4] An interesting question arises: is there a generalized Weyl transformation which can include Weyl quantization and P– Q quantization as well as Q– P ordered quantization as a whole? The answer is affirmative. In this work, we shall extend the above formalism to s-parameterized Weyl transformation, i.e., we extend formula (1) to
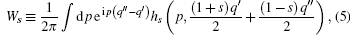 |
where s is an arbitrary real number, and hs(p, q) is another classical corresponding function of the same H(P, Q) and to be determined.
In Section 2, we derive the s-parameterized Wigner operator. Then in Section 3, we present an s-parameterized quantization scheme which includes P– Q quantization, Q– P quantization, and Weyl ordering as its three special cases. At this point we emphasize that our s-parameterized quantization scheme is quite different from the scheme that includes Weyl quantization and normally ordered quantization as well as anti-normally ordered quantization as a whole. In Section 4, we derive the relation between the s-parameterized classical correspondence and the P representation of operators.
Using the inner product ⟨ q′ | q⟩ =δ (q− q′ ), we can reform Eq. (2) as
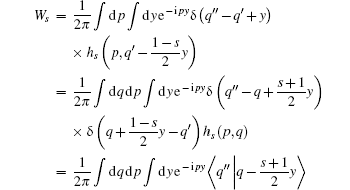 |

from which we can extract
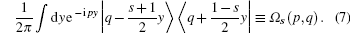 |
Then
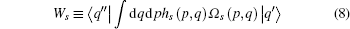 |
and
 |
embody a generalized Weyl quantization scheme, so hs(p, q) is considered as a generalized Weyl classical correspondence of H(P, Q). Using the relation P| q⟩ = id| q⟩ /dq, we can rewrite Eq. (7) as
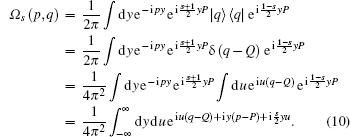 |
In particular, when s = 0, it reduces to Eq. (2) as expected. When s = 1, by applying the Baker– Hausdorff formula to Eq. (10), we have
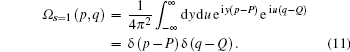 |
However, when s = − 1, Ω s(p, q) becomes the following operator function:
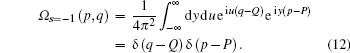 |
Using Eq. (7), we can calculate
 |
With the aid of Eqs. (9) and (13), we can further derive
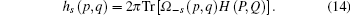 |
As an example, when H(P, Q) = QmPr,
 |
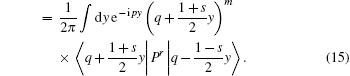
Using the completeness relation of the momentum eigenvector
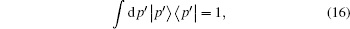 |
we have
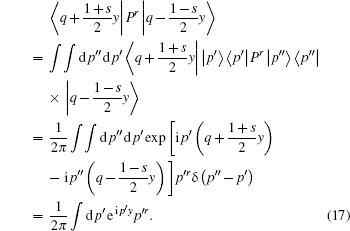 |
Substituting it into Eq. (15) yields the s-parameterized classical correspondence of QmPr
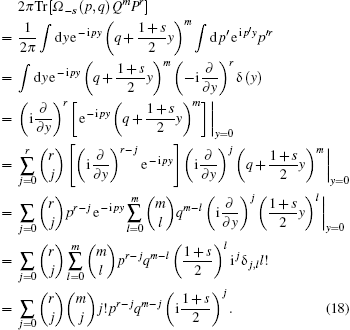 |
In particular, when s = − 1, on the right-hand side only the term of j = 0 survives, so equation (18) reduces to
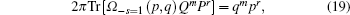 |
which coincides with Eqs. (9) and (12)
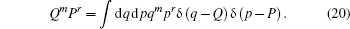 |
On the other hand, when s = 1, equation (18) becomes
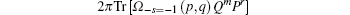 |
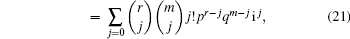
which along with Eqs. (9) and (11) indicates
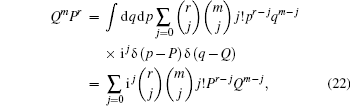 |
which is the operator identity of rearranging QmPr as P– Q ordering. For instance, for m = r = 1, equation (22) becomes QP= PQ + i (we have set ħ = 1).
Now we examine the s-parameterized classical correspondence of 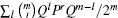
 |
Substituting Eq. (17) into Eq. (23) leads to
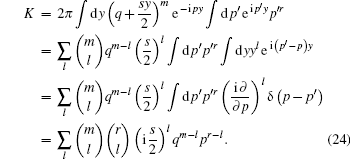 |
For the special case of s = 0, only the term of l = 0 survives, so
 |
which is just the Weyl correspondence. Thus we obtain the generalized s-parameterized quantization scheme rule
 |
For the special case of s = 1,
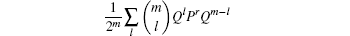 |
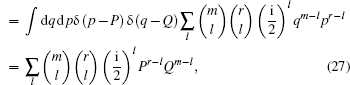
while for s = − 1,
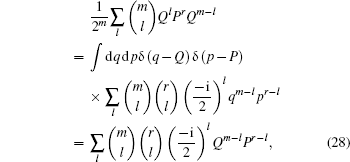 |
these are two new operator identities.
Let 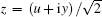

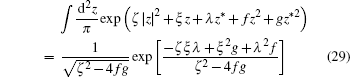 |
with the convergent condition
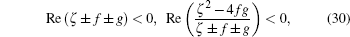 |
we can reform Eq. (9) as
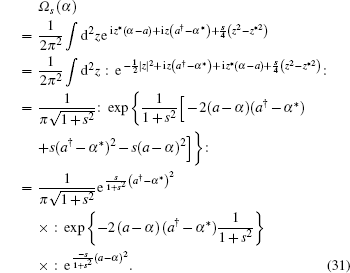 |
Then using the P-represenation 𝔓 (β ) of H(P, Q) [9, 10]
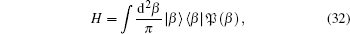 |
we have
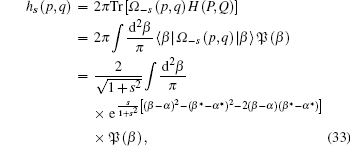 |
which is the relationship between H(P, Q) ′ s P-represenation and its s-parameterized classical correspondence.
In summary, based on the s-parameterized Wigner transformation, we have derived the s-parameterized quantization scheme, which includes P– Q quantization, Q– P quantization, and Weyl ordering as its three special cases and is useful to derive some new operator identities. For the formula converting operators into s-parameterized ordering, we refer to Ref. [11].
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|

