Corresponding author. E-mail: ghanbari@phys.ui.ac.ir
A four-body distorted-wave approximation is applied for theoretical analysis of the fully differential cross sections (FDCS) for proton-impact single ionization of helium atoms in their ground states. The nine-dimensional integrals for the partial amplitudes are analytically reduced to closed-form expressions or some one-dimensional integrals which can be easily calculated numerically. Calculations are performed in the scattering and perpendicular planes. The influence of the target static electron correlations on the process is investigated using a number of different bound-state wave functions for the ground state of the helium targets. An illustrative computation is performed for 75-keV proton-helium collisions and the obtained results are compared with experimental data and other theoretical predictions. Although for small momentum transfers, the comparison shows a reasonable agreement with experiments in the scattering and perpendicular planes, some significant discrepancies are still present at large momentum transfers in these planes. However, our results are compatible and for some cases, better than those of the other sophisticated calculations.
In atomic and molecular physics, ion-impact ionization of few-body systems is an accurate tool to test and identify the electronic structure of the targets.[1, 11] Such reactions also help us to understand the details of the dynamics of collision processes, which may occur in many fields of science and technology. For example, they play a key role in understanding astrophysics, plasma physics, laser physics, radiobiology, and some aspects of biotechnology. However, theoretical description of such rearrangement processes is an important challenging issue. This is due to the fact that in the theoretical study of these phenomena, we at least deal with a three-body problem in which the involved charged particles coupled with infinite-range Coulomb interactions. In addition to some difficulties which may appear in dealing with the long-range potentials, it is well known that the equations governing the dynamic evolution of such systems are not analytically solvable for more than two mutually interacting particles. Consequently, we should seek the approximate solutions of these equations, the validity of which can be examined by comparing with experimental measurements.
Among various ion– atom ionization processes, proton-impact single ionization of helium atoms is a much more fundamental reaction for several reasons. First, helium is the simplest multi-electron atom in nature, which may be used to understand the dynamics of the interactions in multi-particle collision systems. Second, the collision of the proton with the helium atom is a pure four-body problem, which offers a unique opportunity to examine the validity of the theoretical four-body formalisms in explaining the dynamics of such systems. Third, the screening effect of the non-active electrons of the multi-electron atomic targets on the collision dynamics can be studied by using the helium targets. On the other hand, the proton– helium collision system is a proper basic candidate for the study of the inter-electronic correlations existing among the target electrons on the multi-particle scattering systems.
The reasons above have motivated both theoretical and experimental research activities on the proton– helium single ionization process.[5, 6, 9] Using the recoil-ion momentum spectroscopy, [2] the fully differential cross sections (FDCS' s) for this process, which offer more detailed information of the collision dynamics, have been measured by Schulz et al.[5] both in scattering and perpendicular planes. Subsequently, the relatively simple first-Born approximation (FBA)[5] as well as more sophisticated three-body distorted-wave (3DW)[5] and continuum distorted wave-eikonal initial state (CDW-EIS)[6] approximations have been employed to calculate these cross sections. Moreover, a complicated three-Coulomb wave (3CW) model has been applied to study this process. In contrast to numerous theoretical studies that have been conducted on this process, neither of them has been completely satisfactory in comparison with the experiments. On the other hand, a factor which may affect the results of theoretical calculations is the existence of the static correlations of the electrons in the target atom. However, to the best of our knowledge, none of these calculations has examined this issue in detail.
In this paper, a theoretical study of the proton-impact single ionization of helium atoms is presented. Our goal is twofold. (i) To outline a simple four-body distorted wave model to predict the FDCSs which exhibit most of the features observed in their corresponding experimental values. This model is much simpler than that, and at the same time compatible with the 3DW, CDW-EIS, and 3CW theories. (ii) To examine the influence of the static electronic correlations on the FDCSs of the specified reaction.
This paper is organized as follows. Section 2 presents the proposed theoretical model. The nine-dimensional integrals for the partial amplitudes have been reduced to the closed form expressions or to some one-dimensional integrals, which can quickly be evaluated numerically. Section 3 shows the results and the relevant discussion, and Section 4 includes the summary and concluding remarks. Atomic units are used unless otherwise stated.
A four-body collision is considered in which a projectile ion P of charge ZP and mass MP is incident on a target consisting of two active electrons e1 and e2 and a target ion T of nuclear charge ZT = 2 and mass MT. Let s1 and s2 (x1 and x2) be position vectors of the first and second electrons e1 and e2 relative to the target nucleus T (projectile ion P), and S be the position vector of P relative to T. It is assumed that the collision process leads to the single ionization of the target atom. For such a reaction, the T matrix in a first-order approximation is defined as
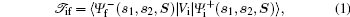 |
where the perturbation potential Vi in the initial channel is given by
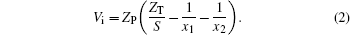 |
For ZT = 2, since Vi vanishes at asymptotic distances (S → ∞ ), the Coulomb distortion of the initial wave function is removed. Consequently, the whole-system initial wave function 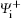
 |
where Ki is the initial wave vector for the relative motion of P with respect to T in the center of mass frame and ϕ i(s1, s2) is the initial bound state wave function of the target atom in its ground state. Since an exact bound-state wave function for the two-electron atomic target is not available, one can use different variational wave functions with different levels of accuracy to describe the initial state of the active electrons. Consequently, the obtained results for transition amplitude and the resultant cross section are likely to be sensitive to a concrete choice of the wave function. In order to investigate this issue and for computational purposes, we assume that the initial bound-state wave function is
 |
where 𝒩 1 and 𝒩 2 are the normalization constants and parameters ζ 1 and ζ 2 are known for the chosen wave function.
The final-state wave function can be approximated in different approaches. Here, a first-Born approximation with two Coulomb waves (FBA-2CW) is adopted to analyze the specified reaction problem. In this approach, both the scattered projectile ion and the ejected electron are described by the Coulomb waves. Therefore, the whole-system final-state wave function reads
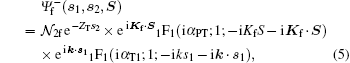 |
where 1F1(a; b; z) is the confluent hypergeometric function, Kf is the final wave vector for the relative motion of P with respect to T in the center of mass frame, k is the momentum vector for the ejected electron e1, and the Sommerfield parameters are α PT = ZPZe/Kf and α T1 = – Ze/k with Ze being the effective charge of the residual ion. The second electron, e2, remains bound to the target nucleus T and is described by a ground-sate hydrogen-like wave function with charge ZT, i.e., 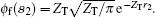
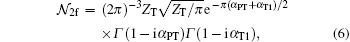 |
where Γ (z) is Euler' s gamma function.
Within the framework of FBA-2CW, the direct amplitude for the single ionization process is given by the sum of the three partial amplitudes corresponding to different two-body perturbative interactions in the initial channel. Each partial amplitude is a nine-dimensional integral in the coordinate representation. These integrals can be derived by inserting the explicit form of the initial perturbation potential Vi as well as the undistorted initial and the distorted final wave functions into Eq. (1). Here, we reduce these integrals to some analytical or one-dimensional integrals which can be easily evaluated. To this end, we note that the transition amplitude can be written as
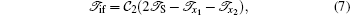 |
with 
 |
where R ≡ S, x1, x2, and η = ζ 2 + ZT. It is obvious that x1 = S – s1 and x2 = S – s2. Also, the momentum transfer vector q is the difference between the incoming and scattered projectile momentum, q = Ki – Kf.
In order to derive a closed-form expression for 𝒯 S, we notice that the integration over s2 can be performed by using the integral identity
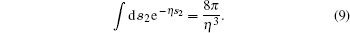 |
Also, the integrations over s1 and S can be evaluated as two special cases of the Nordsieck integral, [12]
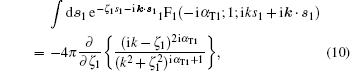 |
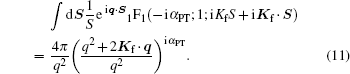 |
Consequently, we have
 |
Similarly, it is possible to reduce the partial amplitude 𝒯 x1 to a one-dimensional integral. To this end, using Eq. (9) and employing the integral identity
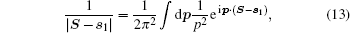 |
we have
 |
In this stage, the contour integral representation of the confluent hypergeometric function, used by Nordsieck, [12]
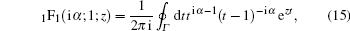 |
would be useful. The integration contour Γ is closed and encircles each of the two points 0 and 1 once anticlockwise. There is a branch cut from 0 to 1. Applying this representation, 𝒯 x1 can be expressed as
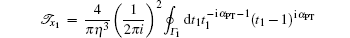 |
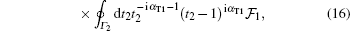
where
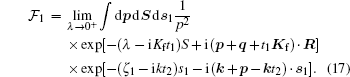 |
The integrations over S and s1 can be performed to obtain
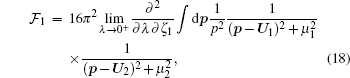 |
where
 |
The three-dimensional integral over p is a Lewis integral, [13] which can be reduced to a one-dimensional integral as
 |
with
 |
In order to perform t1 and t2 integrations analytically, we recast this integral as a linear function of t1 and t2 to obtain
 |
where 𝒜 , ℬ , 𝒞 , and 𝒟 are functions of x
 |
Substituting Eq. (22) into Eq. (16) and employing the procedure explained in the analytical work of Ghanbari– Adivi and Ghavaminia, [14, 15] the contour integrations over t1 and t2 can analytically be performed. The result is
 |
where 2F1(a, b; c; z) is the Gaussian hypergeometric function. By virtue of the relation
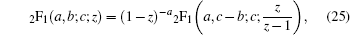 |
equation (24) can be written as
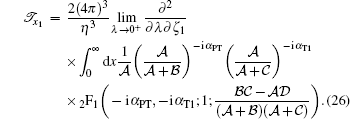 |
The Gaussian hypergeometric function in Eq. (26) is symmetric with respect to α PT and α T1 and is much more convenient for numerical computations.
The partial amplitude 𝒯 x2 takes a simple form by integrating over s1 using Eq. (10). For the remaining integral, using the integral identities (13) and (15), we have
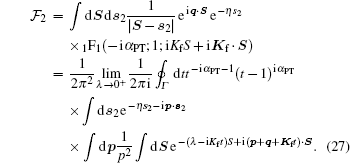 |
Integrations over S and s2 can be carried out using the integral identity
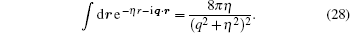 |
Substituting the obtained results into Eq. (27) leads to
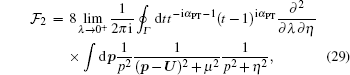 |
where U = − q − Kft and μ = λ − iKft. Using the Lewis integral, this integral can be reduced to
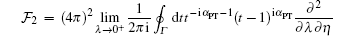 |
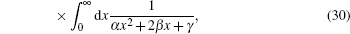
with
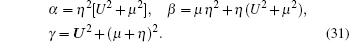 |
We recast the dominator of the integrand as a linear function of t
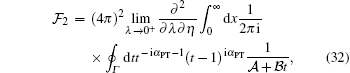 |
with
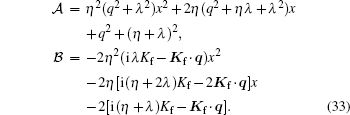 |
Finally, contour integrating over t leads to
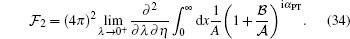 |
Then, we have the following expression for the partial amplitude 𝒯 s2:
 |
By inserting the three calculated partial amplitudes given by Eqs. (12), (24), and (35) into Eq. (7), we find the total FBA-2CW transition amplitude.
In the center-of-mass frame, the FDCS corresponding to the transition amplitude 𝒯 if is given by[1]
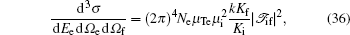 |
where dEe is the energy interval of the ejected electron, dΩ e and dΩ f denote, respectively, the differential solid angles with respect to Ki for the ionized electron and the scattered projectile, and Ne is the number of the initial equivalent electrons in the atomic shell. The μ Te is the reduced mass of the ionized electron and the residual ion in the final channel, and μ i is the reduced mass of the whole collision system in its initial channel.
In this section, the calculated FDCSs for single ionization in 75-keV proton– helium collisions are presented and compared with other theories as well as the corresponding experimental measurements. Calculations are carried out for the scattering and perpendicular planes. The scattering plane is defined by the initial and final momentum vectors of the incoming projectile ion. It is assumed that Ki is along the z axis, and the xz plane is the scattering plane. Therefore, we have Ki = (0, 0, Ki), Kf = (Kfsinθ , 0, Kfcosθ ), and q = (Kfsinθ , 0, Kfcosθ − Ki), where θ is the scattering angle of the projectile. Also, in the scattering plane we have k = (ksinθ e, 0, kcosθ e), while in the perpendicular plane k = (0, ksinθ e, k cosθ e). Electron emission angle θ e is the polar angle of k relative to the initial projectile beam direction (the z axis). Since in both cases qy=0, qx is equivalent to the transverse component qt.
In order to investigate the influence of the static electron correlations on the ionization process, we calculate the FDCSs using three different wave functions to describe the helium atoms in their ground states. These wave functions are: i) the uncorrelated one-parameter Hylleraas wave function, [16]ϕ i(s1, s2)= (α 3/π )e-α (s1+ s2) with α = ZT-5/16; ii) the correlated two-parameter wave function of Silverman et al., [17]ϕ i(s1, s2)= (N/4π )(e-α s1+ β s2+ e-β s1+ α s2), with α = 2.183171, β = 1.188530$ , and N = 8.90868; and iii) the highly correlated four-parameter Byron and Joachain wave function, [18]ϕ i(s1, s2)= (1/4π )(Ae-α s1 + Be-β s1)(Ae-α s2+ Be-β s2), with A = 2.60505, B = 2.08144 , α = 1.41, and β = 2.61.
Figure 1 shows the angular distribution of the FDCSs for electrons with an energy of 5.4 eV ejected into both the scattering (Fig. 1(a)) and perpendicular (Fig. 1(b)) planes in 75-keV proton– helium collisions. The results are calculated using the above-mentioned wave functions for transverse momentum transfers qt of 0.13, 0.41, 0.73, and 1.38 a.u., and are compared with their experimental values reported by Schulz et al.[5] For ejection into the scattering plane, the main feature exhibited by the theoretical curves is the prediction of a pronounced peak in the direction of q. This strong peak structure can be explained in terms of a binary interaction between the projectile and the ejected electron, while both the passive electron e2 and the target ion T are considered as the spectators. This peak is called the “ binary peak” . The angular location for occurrence of the binary peak is given theoretically by θ q = cos– 1(qz/q). As seen from the figure, all the curves show the binary peak in the expected angular region and are in good agreement with the experiment, especially for qt = 0.41 and 0.73 a.u. Also, in the scattering plane, for small qt the binary peak appears at a small angle, as qt increases the binary peak shifts toward the larger angles. For this case, the maximum discrepancy between the curves occurs at the binary peak region. This means that for the binary peak region, the static electronic correlation has a significant influence on the ionization process, while in the other angular regions, the difference of the curves is marginal. Therefore, in these regions, the ionization is an uncorrelated process.
A second smaller peak structure which occurs in the opposite direction of q for electron and fast ion impact is called the “ recoil peak” . This peak structure is due to a two-step scattering mechanism. First, the active electron is kicked by the projectile in the direction of q and then is backscattered by the residual ion in the opposite direction. This peak structure is absent in the reported experimental data and our theoretical calculations.
For all the considered values of qt in the perpendicular plane, the present FDCSs exhibit a strong peak at θ e = 0. With increasing qt, this maximum becomes increasingly broader. In the experimental data for the largest qt, this peak eventually separates into two peaks at about θ e = ± 30° , leaving a minimum at θ e = 0° . This feature which is a clear signature of the higher-order effects, is not exhibited in our first-order predictions. For the angular region around θ e = 0° where the mentioned peak occurs, the discrepancy between the curves is marginal. This is also true for other angular scattering regions. In other words, for ejection into the perpendicular plane, the static correlation plays a minor role in the electron ejection process. Also, the experimentally observed complex structure in the angular region between θ e = − 60° and θ e = + 60° for large qt, the agreement of the theory with the experimental data is not good, neither in shape nor in magnitude.
Figure 2 compares the present results obtained by using the Byron– Joachain wave function in the scattering plane with those of the other complicated theories such as 3DW, [5] CDW-EIS, [6] and 3CW, [9] for electron ejection into the scattering plane. We find that most of the features presented by these complicated theories are also exhibited in our calculations. However, there are some advantages and disadvantages of the present theory in comparison with the others. The present computations are very fast and economic in time relative to 3DW, CDW-EIS, and 3CW theories. The magnitude of the present obtained cross sections is very close to the experimental values, while the 3DW calculations have been multiplied by 0.2 (0.13 a.u.), 0.3 (0.41 a.u.), and 0.6 (0.73 a.u.), and 3CW calculations have been multiplied by 0.35 (0.13 a.u.), 0.55 (0.41 a.u.), 1.18 (0.73 a.u.), and 2 (1.38 a.u.), respectively. Present results are compatible with those of the CDW-EIS, but for the large value of qt = 1.38, our results show a better agreement with the measured data in the angular region between − 90° and 60° . The situation inverses for other angles. For ejection angles between 90° and 270° and for the small values of qt, the present results show a small peak structure which is absent both in experiments and in other theories. This peak disappears as qt increases.
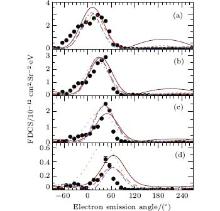 | Fig. 2. Present FDCS calculated for single ionization of helium by 75-keV protons in the scattering plane are compared with their measured values as well as their corresponding values obtained from other theories. The electron emission energy and the transverse momentum transfers are the same as in Fig. 1. The present results are obtained using the Byron– Joachain wave function for helium targets. Solid lines: FBA-2CW. Dashed lines: 3DW calculations multiplied by 0.2 (0.13 a.u.), 0.3 (0.41 a.u.), and 0.6 (0.73 a.u.), respectively. Dash-dotted lines: 3CW calculations multiplied by 0.35 (0.13 a.u.), 0.55 (0.41 a.u.), 1.18 (0.73 a.u.), and 2 (1.38 a.u.), respectively. Dotted lines: CDW-EIS. Solid circles are for experimental data. |
Figure 3 is the same as Fig. 2 but for the electron emission into the perpendicular plane. The FBA calculations[5] are also depicted in this figure. For comparison in shape, the 3DW and 3CW calculated values are multiplied by the same values accounted in the previous paragraph. Also, the FBA calculations are multiplied by 0.4 (0.13 a.u.) and 0.6 (0.41 a.u.), respectively. This shows that there is a significant difference in magnitude of the 3DW, 3CW, and FBA results as compared to the experimental data. This is an important advantage for the present calculations, which are close to experimental measurements in magnitude. In fact, as investigated in Ref. [5], the magnitude can be extremely sensitive to the description of the interaction between the active (ejected) and passive electron which remains bound in the ground state of the target core ion. It seems that using two Coulomb waves for this description is more suitable than one Coulomb wave (FBA) and three Coulomb waves (3CW). In addition to the reasonable agreement with the experiments in magnitude for smaller values of qt, the present calculations give a good description of that data in shape, especially for the observed pronounced peak around θ e = 0° . In particular, it seems that the present calculation gives a better description of the collision dynamics for qt = 0.13, 0.41, and 0.73 a.u. in the peak region in comparison with more successful CDW– EIS theory. However, for the scattering angles beyond θ e = 80° , the CDW– EIS theory is in a better agreement with the measurements. For qt = 1.38, none of the theories gives a reasonable description of the measured data, both in shape and in magnitude.
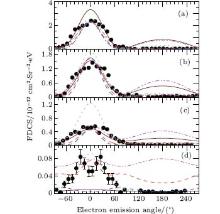 | Fig. 3. Same as Fig. 2 but for the perpendicular plane. Dash-dot-dotted lines: FBA multiplied by 0.4 (0.13 a.u.) and 0.6 (0.41 a.u.), respectively. |
We have applied a first-order four-body distorted wave formalism to treat single-electron ionization of atoms by protons. Using three different ground-state wave functions for helium targets, the FDCSs were calculated and compared with each other as well as the experimental data. After comparison, we find that in the binary-peak region, the static electron correlation plays a significant role in the electron ejection into the scattering plane. However, for the other angular regions as well as the ejection into the perpendicular plane, this factor plays a minor role. Also, the obtained results are compared with the other complicated theories. It is shown that the present theory gives reasonably satisfactory results for ejection into the angular region around the binary peak in the scattering plane and into the angular region around the pronounced peak in the perpendicular plane. However, the situation for qt = 1.38 is an exception. For this value of qt, the higher-order effects are dominant and the first-order predictions are found to be very unsatisfactory. Among the various theories discussed in this paper, the best description of the measurements for qt = 1.38 in the perpendicular plane is given by the CDW– EIS approach. For other values of qt, overall agreement between the present theory and experiment is reasonably good and is better than other theories in some cases and some angular regions.
One of the authors, S. Eskandari, wishes to acknowledge the office of graduate studies at the University of Isfahan for their support and research facilities.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|


